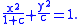In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the foci (icon; singular focus) are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic section

Conic section

In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...

s, the four types of which are the circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

, ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

, parabola

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

, and hyperbola

Hyperbola

In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...

. In addition, foci are used to define the Cassini oval

Cassini oval

A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...

 and the Cartesian oval

Cartesian oval

In geometry, a Cartesian oval, named after René Descartes, is determined as follows. Let and be fixed points in the plane, and let and denote the Euclidean distances from these points to a third variable point . Let and be arbitrary real numbers. Then the Cartesian oval is the locus of...

.

Defining conics in terms of two foci

An ellipse can be defined as the locus

Locus (mathematics)

In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....

 of points for each of which the sum of the distances to two given foci is a constant.

A circle is the special case of an ellipse in which the two foci coincide with each other. Thus, a circle can be more simply defined as the locus of points each of which is a fixed distance from a single given focus. A circle can also be defined as the circle of Apollonius

Circles of Apollonius

The term circle of Apollonius is used to describe several types of circles associated with Apollonius of Perga, a renowned Greek geometer. Most of these circles are found in planar Euclidean geometry, but analogs have been defined on other surfaces; for example, counterparts on the surface of a...

, in terms of two different foci, as the set of points having a fixed ratio of distances to the two foci.

A parabola is a limiting case of an ellipse in which one of the foci is a point at infinity.

A hyperbola can be defined as the locus of points for each of which the absolute value of the difference between the distances to two given foci is a constant.

Defining conics in terms of a focus and a directrix

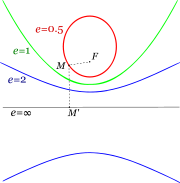
It is also possible to describe all the conic sections in terms of a single focus and a single directrix, which is a given line not containing the focus. A conic is defined as the locus of points for each of which the distance to the focus divided by the distance to the directrix is a fixed positive constant, called the eccentricity e. If e is between zero and one the conic is an ellipse; if e=1 the conic is a parabola; and if e>1 the conic is a hyperbola. If the distance to the focus is fixed and the directrix is a line at infinity

Line at infinity

In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...

, so the eccentricity is zero, then the conic is a circle.

Defining conics in terms of a focus and a directrix circle

It is also possible to describe all the conic sections as loci of points that are equidistant from a single focus and a single, circular directrix. For the ellipse, both the focus and the center of the directrix circle have finite coordinates and the radius of the directrix circle is greater than the distance between the center of this circle and the focus; thus, the focus is inside the directrix circle. The ellipse thus generated has its second focus at the center of the directrix circle, and the ellipse lies entirely within the circle.

For the parabola, the center of the directrix moves to the point at infinity (see projective geometry

Projective geometry

In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...

). The directrix 'circle' becomes a curve with zero curvature, indistinguishable from a straight line. The two arms of the parabola become increasingly parallel as they extend, and 'at infinity' become parallel; using the principles of projective geometry, the two parallels intersect at the point at infinity and the parabola becomes a closed curve (elliptical projection).

To generate a hyperbola, the radius of the directrix circle is chosen to be less than the distance between the center of this circle and the focus; thus, the focus is outside the directrix circle. The arms of the hyperbola approach asymptotic lines and the 'right-hand' arm of one branch of a hyperbola meets the 'left-hand' arm of the other branch of a hyperbola at the point at infinity; this is based on the principle that, in projective geometry, a single line meets itself at a point at infinity. The two branches of a hyperbola are thus the two (twisted) halves of a curve closed over infinity.

In projective geometry, all conics are equivalent in the sense that every theorem that can be stated for one can be stated for the others.

Astronomical significance

In the gravitation

Gravitation

Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...

al two-body problem

Two-body problem

In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...

, the orbits of the two bodies are described by two overlapping conic sections each with one of their foci being coincident at the center of mass

Center of mass

In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...

 (barycenter

Barycentric coordinates (astronomy)

In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...

).

Cartesian and Cassini ovals

A Cartesian oval

Cartesian oval

In geometry, a Cartesian oval, named after René Descartes, is determined as follows. Let and be fixed points in the plane, and let and denote the Euclidean distances from these points to a third variable point . Let and be arbitrary real numbers. Then the Cartesian oval is the locus of...

 is the set of points for each of which the weighted sum of the distances to two given foci is a constant. If the weights are equal, the special case of an ellipse results.

A Cassini oval

Cassini oval

A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...

 is the set of points for each of which the product of the distances to two given foci is a constant.

Generalization

The concept of a focus can be generalized to arbitrary algebraic curves. Let C be a curve of class m and let I and J denote the circular points at infinity

Circular points at infinity

In projective geometry, the circular points at infinity in the complex projective plane are and ....

. Draw the m tangents to C through each of I and J. There are two sets of m lines which will have m² points of intersection, with exceptions in some cases due to singularities, etc. These points of intersection are the defined to be the foci of C. In other words, a point P is a focus if both PI and PJ are tangent to C. When C is a real curve, only the intersections of conjugate pairs are real, so there are m in a real foci and m²−m imaginary foci. When C is a conic, the real foci defined this way are exactly the foci which can be used in the geometric construction of C.

Confocal curves

Let P₁, P₂, …, P_m be given as foci of a curve C of class m. Let P be the product of the tangential equations of these points and Q the product of the tangential equations of the circular points at infinity. Then all the lines which are common tangents to both P=0 and Q=0 are tangent to C. So, by the AF+BG theorem

AF+BG theorem

In algebraic geometry, a field of mathematics, the AF+BG theorem is a result of Max Noether which describes when the equation of an algebraic curve in the complex projective plane can be written in terms of the equations of two other algebraic curves....

, the tangential equation of C has the form HP+KQ=0. Since C has class m, H must be a constant and K but have degree less than or equal to m−2. The case H=0 can be eliminated as degenerate, so the tangential equation of C can be written as P+fQ=0 where f is an arbitrary polynomial of degree m−2.

For example, let P₁=(1,0), P₂=(−1,0). The tangential equations are X+1=0 and X−1=0 so P= X²-1=0. The tangential equations for the circular points at infinity are X+iY=0 and X−iY=0 so Q=X²+Y². Therefore the tangential equation for a conic with the given foci is X²-1+c(X²+Y²)=0, or (1+c)X²+cY²=1 where c is an arbitrary constant. In point coordinates this becomes