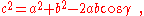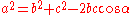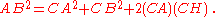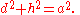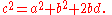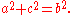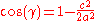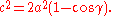Law of cosines - AbsoluteAstronomy.com

Trigonometry

Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...

, the law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a plane triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

to the cosine of one of its angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

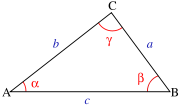
s. Using notation as in Fig. 1, the law of cosines says

where γ denotes the angle contained between sides of lengths a and b and opposite the side of length c.

The law of cosines generalizes the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

, which holds only for right triangles: if the angle γ is a right angle (of measure 90°

Degree (angle)

A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...

or π/2 radians), then cos(γ) = 0, and thus the law of cosines reduces to the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known, and in computing the angles of a triangle if all three sides are known.

By changing which sides of the triangle play the roles of a, b, and c in the original formula, one discovers that the following two formulas also state the law of cosines:

Though the notion of cosine was not yet developed in his time, Euclid

Euclid

Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...

's Elements

Euclid's Elements

Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...

, dating back to the 3rd century BC, contains an early geometric theorem equivalent to the law of cosines. The case of obtuse triangle and acute triangle (corresponding to the two cases of negative or positive cosine) are treated separately, in Propositions 12 and 13 of Book 2. Trigonometric functions and algebra (in particular negative numbers) being absent in Euclid's time, the statement has a more geometric flavor:

Proposition 12

In obtuse-angled triangles the square on the side subtending the obtuse angle is greater than the squares on the sides containing the obtuse angle by twice the rectangle contained by one of the sides about the obtuse angle, namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the obtuse angle. — Euclid's Elements, translation by Thomas L. Heath.http://www.perseus.tufts.edu/cgi-bin/ptext?doc=Perseus%3Atext%3A1999.01.0086&query=head%3D%2398&chunk=book

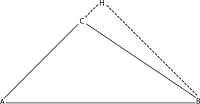
Using notation as in Fig. 2, Euclid's statement can be represented by the formula

This formula may be transformed into the law of cosines by noting that CH = (CB) cos(π – γ) = −(CB) cos(γ). Proposition 13 contains an entirely analogous statement for acute triangles.

It was not until the development of modern trigonometry

Trigonometry

in the Middle Ages

Middle Ages

The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...

, especially the discovery of the cosine, that the general law of cosines was formulated. The Persian astronomer

Islamic astronomy

Islamic astronomy or Arabic astronomy comprises the astronomical developments made in the Islamic world, particularly during the Islamic Golden Age , and mostly written in the Arabic language. These developments mostly took place in the Middle East, Central Asia, Al-Andalus, and North Africa, and...

and mathematician al-Battani

Al-Battani

Abū ʿAbd Allāh Muḥammad ibn Jābir ibn Sinān al-Raqqī al-Ḥarrānī al-Ṣābiʾ al-Battānī was a Muslim astronomer, astrologer, and mathematician...

generalized Euclid's result to spherical geometry

Spherical geometry

Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....

at the beginning of the 10th century, which permitted him to calculate the angular distances between stars. In the 15th century, al-Kashi Persian mathematician in Samarqand computed trigonometric tables to great accuracy and provided the first explicit statement of the law of cosines in a form suitable for triangulation

Triangulation

In trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...

. In France

France

The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...

, the law of cosines is still referred to as the theorem of Al-Kashi.

The theorem was popularised in the Western world

Western world

The Western world, also known as the West and the Occident , is a term referring to the countries of Western Europe , the countries of the Americas, as well all countries of Northern and Central Europe, Australia and New Zealand...

by François Viète

François Viète

François Viète , Seigneur de la Bigotière, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to its innovative use of letters as parameters in equations...

in the 16th century. At the beginning of the 19th century, modern algebraic notation allowed the law of cosines to be written in its current symbolic form.

Applications

The theorem is used in triangulation

Triangulation

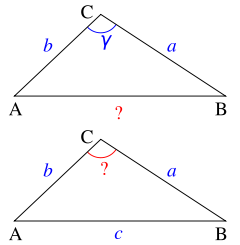
, for solving a triangle, i.e., to find (see Figure 3):

the third side of a triangle if one knows two sides and the angle between them:

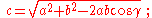
the angles of a triangle if one knows the three sides:

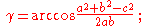
the third side of a triangle if one knows two sides and an angle opposite to one of them (one may also use the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

to do this if it is a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...

):

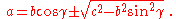
These formulas produce high round-off error

Round-off error

A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...

s in floating point

Floating point

In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...

calculations if the triangle is very acute, i.e., if c is small relative to a and b or γ is small compared to 1. It is even possible to obtain a result slightly greater than one for the cosine of an angle.

The third formula shown is the result of solving for a the quadratic equation

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

a² − 2ab cos γ + b² − c² = 0. This equation can have 2, 1, or 0 positive solutions corresponding to the number of possible triangles given the data. It will have two positive solutions if b sin(γ) < c < b, only one positive solution if c ≥ b or c = b sin(γ), and no solution if c < b sin(γ). These different cases are also explained by the Side-Side-Angle congruence

Congruence (geometry)

In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

ambiguity.

Using the distance formula

Consider a triangle with sides of length a, b, c, where γ is the measurement of the angle opposite the side of length c. We can place this triangle on the coordinate system by plotting

By the distance formula, we have

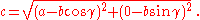
Now, we just work with that equation:

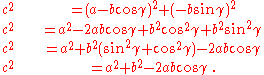
An advantage of this proof is that it does not require the consideration of different cases for when the triangle is acute vs. obtuse.

Using trigonometry

Drop the perpendicular

Perpendicular

In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

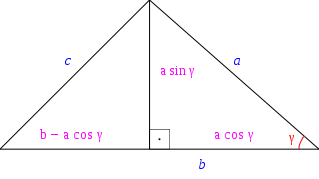
onto the side c to get (see Fig. 4)

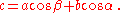
(This is still true if α or β is obtuse, in which case the perpendicular falls outside the triangle.) Multiply through by c to get

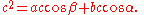
By considering the other perpendiculars obtain

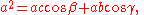
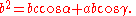
Adding the latter two equations gives

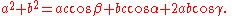
Subtracting the first equation from the last one we have

which simplifies to

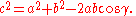
This proof uses trigonometry

Trigonometry

in that it treats the cosines of the various angles as quantities in their own right. It uses the fact that the cosine of an angle expresses the relation between the two sides enclosing that angle in any right triangle. Other proofs (below) are more geometric in that they treat an expression such as a cos(γ) merely as a label for the length of a certain line segment.

Many proofs deal with the cases of obtuse and acute angles γ separately.

Using the Pythagorean theorem

Case of an obtuse angle. Euclid

Euclid

Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...

proves this theorem by applying the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

to each of the two right triangles in Fig. 5. Using d to denote the line segment CH and h for the height BH, triangle AHB gives us

and triangle CHB gives us

Expanding

Polynomial expansion

In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition...

the first equation gives us

Substituting the second equation into this, the following can be obtained

This is Euclid's Proposition 12 from Book 2 of the Elements

Euclid's Elements

. To transform it into the modern form of the law of cosines, note that

Case of an acute angle. Euclid's proof of his Proposition 13 proceeds along the same lines as his proof of Proposition 12: he applies the Pythagorean theorem to both right triangles formed by dropping the perpendicular onto one of the sides enclosing the angle γ and uses the binomial theorem to simplify.

Another proof in the acute case. Using a little more trigonometry, the law of cosines by applying can be deduced by using the Pythagorean theorem only once. In fact, by using the right triangle on the left hand side of Fig. 6 it can be shown that:

using the trigonometric identity

Remark. This proof needs a slight modification if b < a cos(γ). In this case, the right triangle to which the Pythagorean theorem is applied moves outside the triangle ABC. The only effect this has on the calculation is that the quantity b − a cos(γ) is replaced by a cos(γ) − b. As this quantity enters the calculation only through its square, the rest of the proof is unaffected.
Note. This problem only occurs when β is obtuse, and may be avoided by reflecting the triangle about the bisector of γ.

Observation. Referring to Fig 6 it's worth noting that if the angle opposite side a is

then:

This is useful for direct calculation of a second angle when two sides and an included angle are given.

Using Ptolemy's theorem

Referring to the diagram, triangle ABC with sides AB = c, BC = a and AC = b is drawn inside its circumcircle as shown. Triangle ABD is constructed congruent to triangle ABC with AD = BC and BD = AC. Perpendiculars from D and C meet base AB at E and F respectively. Then:

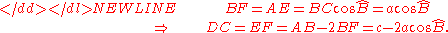
Now the law of cosines is rendered by a straightforward application of Ptolemy's theorem to cyclic quadrilateral

Cyclic quadrilateral

In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...

ABCD:

Plainly if angle B is 90 degrees, then ABCD is a rectangle and application of Ptolemy's theorem yields Pythagoras' theorem:

By comparing areas

One can also prove the law of cosines by calculating area

Area

Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

s. The change of sign as the angle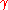

becomes obtuse makes a case distinction necessary.

Recall that

a², b², and c² are the areas of the squares with sides a, b, and c, respectively;
if γ is acute, then ab cos(γ) is the area of the parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...

with sides a and b forming an angle of ;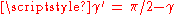
if γ is obtuse, and so cos(γ) is negative, then −ab cos(γ) is the area of the parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...

with sides a' and b forming an angle of .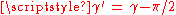

Acute case. Figure 7a shows a heptagon cut into smaller pieces (in two different ways) to yield a proof of the law of cosines. The various pieces are

in pink, the areas a², b² on the left and the areas 2ab cos(γ) and c² on the right;
in blue, the triangle ABC, on the left and on the right;
in grey, auxiliary triangles, all congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

to ABC, an equal number (namely 2) both on the left and on the right.

The equality of areas on the left and on the right gives

Obtuse case. Figure 7b cuts a hexagon in two different ways into smaller pieces, yielding a proof of the law of cosines in the case that the angle γ is obtuse. We have

in pink, the areas a², b², and −2ab cos(γ) on the left and c² on the right;
in blue, the triangle ABC twice, on the left, as well as on the right.

The equality of areas on the left and on the right gives

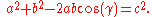
The rigorous proof will have to include proofs that various shapes are congruent

Congruence (geometry)

In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

and therefore have equal area. This will use the theory of congruent triangles.

Using geometry of the circle

Using the geometry of the circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

, it is possible to give a more geometric

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

proof than using the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

alone. Algebraic

Elementary algebra

Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...

manipulations (in particular the binomial theorem

Binomial theorem

In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...

) are avoided.

Case of acute angle γ, where a > 2b cos(γ). Drop the perpendicular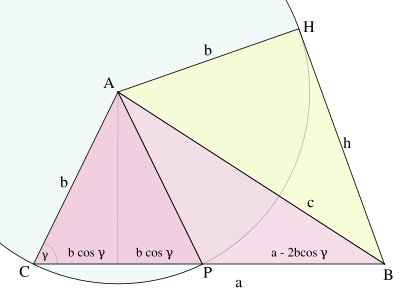

Perpendicular

In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

from A onto a = BC, creating a line segment of length b cos(γ). Duplicate the right triangle to form the isosceles triangle ACP. Construct the circle

Circle

with center A and radius b, and its tangent h = BH through B. The tangent h forms a right angle with the radius b (Euclid's Elements: Book 3, Proposition 18; or see here), so the yellow triangle in Figure 8 is right. Apply the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

to obtain

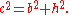
Then use the tangent secant theorem (Euclid's Elements: Book 3, Proposition 36), which says that the square on the tangent through a point B outside the circle is equal to the product of the two lines segments (from B) created by any secant

Secant line

A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...

of the circle through B. In the present case: BH² = BC BP, or

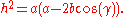
Substituting into the previous equation gives the law of cosines:

Note that h² is the power

Power of a point

In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle C of radius r is defined...

of the point B with respect to the circle. The use of the Pythagorean theorem and the tangent secant theorem can be replaced by a single application of the power of a point theorem.

Case of acute angle γ, where a < 2b cos γ. Drop the perpendicular

Perpendicular

In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

from A onto a = BC, creating a line segment of length b cos(γ). Duplicate the right triangle to form the isosceles triangle ACP. Construct the circle

Circle

with center A and radius b, and a chord

Chord (geometry)

A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...

through B perpendicular to c = AB, half of which is h = BH. Apply the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

to obtain

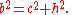
Now use the chord theorem (Euclid's Elements: Book 3, Proposition 35), which says that if two chords intersect, the product of the two line segments obtained on one chord is equal to the product of the two line segments obtained on the other chord. In the present case: BH² = BC BP, or

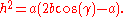
Substituting into the previous equation gives the law of cosines:

Note that the power of the point B with respect to the circle has the negative value −h².

Case of obtuse angle γ. This proof uses the power of a point theorem directly, without the auxiliary triangles obtained by constructing a tangent or a chord. Construct a circle with center B and radius a (see Figure 9), which intersects the secant

Secant line

through A and C in C and K. The power

Power of a point

of the point A with respect to the circle is equal to both AB² − BC² and AC·AK. Therefore,

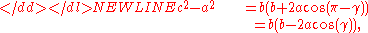
which is the law of cosines.

Using algebraic measures for line segments (allowing negative numbers as lengths of segments) the case of obtuse angle (CK > 0) and acute angle (CK < 0) can be treated simultaneously.

Vector formulation

The law of cosines is equivalent to the formula

in the theory of vectors, which expresses the dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

of two vectors in terms of their respective lengths and the angle

Angle

they enclose.

Proof of equivalence. Referring to Figure 10, note that

and so we may calculate:

The law of cosines formulated in this notation states:

which is clearly equivalent to the above formula from the theory of vectors.

Isosceles case

When a = b, i.e., when the triangle is isosceles with the two sides incident to the angle γ equal, the law of cosines simplifies significantly. Namely, because a² + b² = 2a² = 2ab, the law of cosines becomes

Analog for tetrahedra

An analogous statement begins by taking

to be the areas of the four faces of a tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

. Denote the dihedral angle

Dihedral angle

In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...

s by

etc. Then

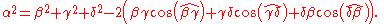
Law of cosines in non-Euclidean geometry

A version of the law of cosines also holds in non-Euclidean geometry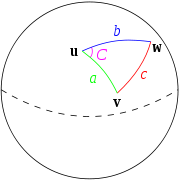

Non-Euclidean geometry

Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...

. In spherical geometry

Spherical geometry

, a triangle is defined by three points u, v, and w on the unit sphere, and the arcs of great circle

Great circle

A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...

s connecting those points. If these great circles make angles A, B, and C with opposite sides a, b, c then the spherical law of cosines asserts that each of the following relationships hold:

In hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

, a pair of equations are collectively known as the hyperbolic law of cosines. The first is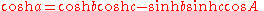

where sinh and cosh are the hyperbolic sine and cosine, and the second is

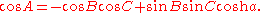
Like in Euclidean geometry, one can use the law of cosines to determine the angles A, B, C from the knowledge of the sides a, b, c. However, unlike Euclidean geometry, the reverse is also possible in each of the models of non-Euclidean geometry: the angles A, B, C determine the sides a, b, c.

External links

Several derivations of the Cosine Law, including Euclid's at cut-the-knot
Cut-the-knot
Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Applications

Using the distance formula

Using trigonometry

Using the Pythagorean theorem

Using Ptolemy's theorem

By comparing areas

Using geometry of the circle

Vector formulation

Isosceles case

Analog for tetrahedra

Law of cosines in non-Euclidean geometry

See also

External links