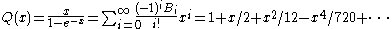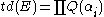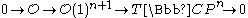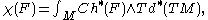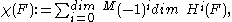Todd class
Encyclopedia
In mathematics
, the Todd class is a certain construction now considered a part of the theory in algebraic topology
of characteristic class
es. The Todd class of a vector bundle
can be defined by means of the theory of Chern class
es, and is encountered where Chern classes exist — most notably in differential topology
, the theory of complex manifold
s and algebraic geometry
. In rough terms, a Todd class acts like a reciprocal of a Chern class, or stands in relation to it as a conormal bundle does to a normal bundle
.
The Todd class plays a fundamental role in generalising the classical Riemann-Roch theorem to higher dimensions, in the Hirzebruch-Riemann-Roch theorem
and Grothendieck-Hirzebruch-Riemann-Roch theorem.
, who introduced a special case of the concept in algebraic geometry in 1937, before the Chern classes were defined. The geometric idea involved is sometimes called the Todd-Eger class.
The general definition in higher dimensions is due to Hirzebruch.
X, it is usually possible to limit the definition to the case of a Whitney sum of line bundle
s, by means of a general device of characteristic class theory, the use of Chern roots (aka, the splitting principle
). For the definition, let
be the formal power series
with the property that the coefficient of xn in Q(x)n+1 is 1 (where the Bi are Bernoulli number
s).
If E has the αi as its Chern roots, then
which is to be computed in the cohomology ring
of X (or in its completion if one wants to consider infinite dimensional manifolds).
The Todd class can be given explicitly as a formal power series in the Chern classes as follows:
where the cohomology classes ci are the Chern classes of E, and lie in the cohomology group H2i(X). If X is finite dimensional then most terms vanish and td(E) is a polynomial in the Chern classes.
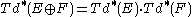
From the Euler exact sequence for the tangent bundle of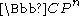
and multiplicativity, one obtains
where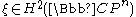
is the fundamental class of the hyperplane section.
F on a smooth
compact complex manifold
M, one has
where
is its holomorphic Euler characteristic,
and Ch*(F) its Chern character.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Todd class is a certain construction now considered a part of the theory in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
of characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es. The Todd class of a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
can be defined by means of the theory of Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
es, and is encountered where Chern classes exist — most notably in differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, the theory of complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. In rough terms, a Todd class acts like a reciprocal of a Chern class, or stands in relation to it as a conormal bundle does to a normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
.
The Todd class plays a fundamental role in generalising the classical Riemann-Roch theorem to higher dimensions, in the Hirzebruch-Riemann-Roch theorem
Hirzebruch-Riemann-Roch theorem
In mathematics, the Hirzebruch–Riemann–Roch theorem, named after Friedrich Hirzebruch, Bernhard Riemann, and Gustav Roch, is Hirzebruch's 1954 result contributing to the Riemann–Roch problem for complex algebraic varieties of all dimensions...
and Grothendieck-Hirzebruch-Riemann-Roch theorem.
History
It is named for J. A. ToddJ. A. Todd
John Arthur Todd FRS was a British geometer. He was born in Liverpool, and went to Trinity College of the University of Cambridge in 1925. He did research under H.F. Baker, and in 1931 took a position at the University of Manchester. He became a lecturer at Cambridge in 1937...
, who introduced a special case of the concept in algebraic geometry in 1937, before the Chern classes were defined. The geometric idea involved is sometimes called the Todd-Eger class.
The general definition in higher dimensions is due to Hirzebruch.
Definition
To define the Todd class td(E) where E is a complex vector bundle on a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, it is usually possible to limit the definition to the case of a Whitney sum of line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s, by means of a general device of characteristic class theory, the use of Chern roots (aka, the splitting principle
Splitting principle
In mathematics, the splitting principle is a technique used to reduce questions about vector bundles to the case of line bundles.In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct...
). For the definition, let
be the formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
with the property that the coefficient of xn in Q(x)n+1 is 1 (where the Bi are Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s).
If E has the αi as its Chern roots, then
which is to be computed in the cohomology ring
Cohomology ring
In mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
of X (or in its completion if one wants to consider infinite dimensional manifolds).
The Todd class can be given explicitly as a formal power series in the Chern classes as follows:
- td(E) = 1 + c1/2 + (c12+c2)/12 + c1c2/24 + (−c14 + 4c12c2 + c1c3 + 3c22 − c4)/720 + ...
where the cohomology classes ci are the Chern classes of E, and lie in the cohomology group H2i(X). If X is finite dimensional then most terms vanish and td(E) is a polynomial in the Chern classes.
Properties of Todd class
The Todd class is multiplicative: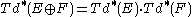From the Euler exact sequence for the tangent bundle of
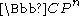
and multiplicativity, one obtains
where
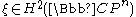is the fundamental class of the hyperplane section.Hirzebruch-Riemann-Roch formula
For any coherent sheafCoherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
F on a smooth
compact complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
M, one has
where
is its holomorphic Euler characteristic,
and Ch*(F) its Chern character.