Thom space
Encyclopedia
In mathematics
, the Thom space, Thom complex, or Pontryagin-Thom construction (named after René Thom
and Lev Pontryagin) of algebraic topology
and differential topology
is a topological space
associated to a vector bundle
, over any paracompact space.
be a rank k real
vector bundle over the paracompact space B. Then for each point b in B, the fiber Fb is a k-dimensional real vector space
. We can form an associated sphere bundle Sph(E) → B by taking the one-point compactification of each fiber separately. Finally, from the total space Sph(E) we obtain the Thom complex T(E) by identifying all the new points to a single point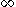
, which we take as the basepoint of T(E).
of fiber bundles. (We have stated the result in terms of Z2 coefficients to avoid complications arising from orientability
.)
Let B, E, and p be as above. Then there is an isomorphism, now called a Thom isomorphism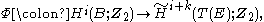
for all i greater than or equal to 0, where the right hand side is reduced cohomology.
We can loosely interpret the theorem as being a generalization of the suspension isomorphism on (co)homology, because the Thom space of a trivial bundle on B of rank k is isomorphic to the kth suspension of B+, B with a disjoint point added.
This theorem was formulated and proved by René Thom
in his 1952 thesis.
:
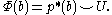
In particular, the Thom isomorphism sends the identity
element of H*(B) to U.
groups could be computed as the homotopy groups of certain Thom spaces MG(n). The proof depends on and is intimately related to the transversality properties of smooth manifolds -- see Thom transversality theorem. By reversing this construction, John Milnor
and Sergei Novikov
(among many others) were able to answer questions about the existence and uniqueness of high-dimensional manifolds: this is now known as surgery theory
. In addition, the spaces MG(n) fit together to form spectra
MG now known as Thom spectra, and the cobordism groups are in fact stable
. Thom's construction thus also unifies differential topology
and stable homotopy theory, and is in particular integral to our knowledge of the stable homotopy groups of spheres.
If the Steenrod operations are available, we can use them and the isomorphism of the theorem to construct the Stiefel-Whitney classes. Recall that the Steenrod operations (mod 2) are natural transformation
s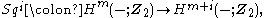
defined for all nonnegative integers m. If i = m, then Sqi coincides with the cup square. We can define the ith Stiefel-Whitney class wi (p) of the vector bundle p : E → B by:
of a smooth manifold, the conclusion of the above is called the Wu formula, and has the following strong consequence: since the Steenrod operations are invariant under homotopy equivalence, we conclude that the Stiefel-Whitney classes of a manifold are as well. This is an extraordinary result that does not generalize to other characteristic classes. There exists a similar famous and difficult result establishing topological invariance for rational Pontryagin classes, due to Sergei Novikov
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Thom space, Thom complex, or Pontryagin-Thom construction (named after René Thom
René Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
and Lev Pontryagin) of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
associated to a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, over any paracompact space.
Construction of the Thom space
One way to construct this space is as follows. Let- p : E → B
be a rank k real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector bundle over the paracompact space B. Then for each point b in B, the fiber Fb is a k-dimensional real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. We can form an associated sphere bundle Sph(E) → B by taking the one-point compactification of each fiber separately. Finally, from the total space Sph(E) we obtain the Thom complex T(E) by identifying all the new points to a single point
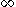, which we take as the basepoint of T(E).The Thom isomorphism
The significance of this construction begins with the following result, which belongs to the subject of cohomologyCohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of fiber bundles. (We have stated the result in terms of Z2 coefficients to avoid complications arising from orientability
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
.)
Let B, E, and p be as above. Then there is an isomorphism, now called a Thom isomorphism
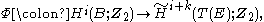
for all i greater than or equal to 0, where the right hand side is reduced cohomology.
We can loosely interpret the theorem as being a generalization of the suspension isomorphism on (co)homology, because the Thom space of a trivial bundle on B of rank k is isomorphic to the kth suspension of B+, B with a disjoint point added.
This theorem was formulated and proved by René Thom
René Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
in his 1952 thesis.
The Thom class
The isomorphism of the theorem is explicitly known: there is a certain cohomology class, the Thom class, in the kth cohomology group of the Thom space. Denote this Thom class by U. Then for a class b in the cohomology of the base, we can compute the Thom isomorphism via the pullback of the bundle projection and the cohomology cup productCup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
:
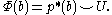
In particular, the Thom isomorphism sends the identity
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
element of H*(B) to U.
Significance of Thom's work
In his 1952 paper, Thom showed that the Thom class, the Stiefel-Whitney classes, and the Steenrod operations were all related. He used these ideas to prove in the 1954 paper Quelques propriétés globales des variétés differentiables that the cobordismCobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
groups could be computed as the homotopy groups of certain Thom spaces MG(n). The proof depends on and is intimately related to the transversality properties of smooth manifolds -- see Thom transversality theorem. By reversing this construction, John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
and Sergei Novikov
Sergei Novikov
Sergey Novikov may refer to:*Sergei Borisovich Novikov , Soviet Russian footballer*Sergei Novikov , Russian mathematician*Sergey Novikov , Belarussian biathlete...
(among many others) were able to answer questions about the existence and uniqueness of high-dimensional manifolds: this is now known as surgery theory
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
. In addition, the spaces MG(n) fit together to form spectra
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
MG now known as Thom spectra, and the cobordism groups are in fact stable
Stable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
. Thom's construction thus also unifies differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
and stable homotopy theory, and is in particular integral to our knowledge of the stable homotopy groups of spheres.
If the Steenrod operations are available, we can use them and the isomorphism of the theorem to construct the Stiefel-Whitney classes. Recall that the Steenrod operations (mod 2) are natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s
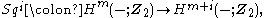
defined for all nonnegative integers m. If i = m, then Sqi coincides with the cup square. We can define the ith Stiefel-Whitney class wi (p) of the vector bundle p : E → B by:
Consequences for differential manifolds
If we take the bundle in the above to be the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a smooth manifold, the conclusion of the above is called the Wu formula, and has the following strong consequence: since the Steenrod operations are invariant under homotopy equivalence, we conclude that the Stiefel-Whitney classes of a manifold are as well. This is an extraordinary result that does not generalize to other characteristic classes. There exists a similar famous and difficult result establishing topological invariance for rational Pontryagin classes, due to Sergei Novikov
Sergei Novikov
Sergey Novikov may refer to:*Sergei Borisovich Novikov , Soviet Russian footballer*Sergei Novikov , Russian mathematician*Sergey Novikov , Belarussian biathlete...
.
See also
- Fiber bundleFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
- Characteristic classes
- CobordismCobordismIn mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
- Cohomology operationCohomology operationIn mathematics, the cohomology operation concept became central to algebraic topology, particularly homotopy theory, from the 1950s onwards, in the shape of the simple definition that if F is a functor defining a cohomology theory, then a cohomology operation should be a natural transformation from...
- Steenrod problemSteenrod problemIn mathematics, and particularly homology theory, Steenrod's Problem is a problem concerning the realisation of homology classes by singular manifolds.-Formulation:...