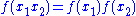
Involution
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an (anti-)involution, or an involutary function, is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f that is its own inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
:
- f(f(x)) = x for all x in the domain of f.
General properties
Any involution is a bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
.
The identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
is a trivial example of an involution. Common examples in mathematics of more detailed involutions include multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
by −1 in arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
, the taking of reciprocals
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
, complementation
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and complex conjugation
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
. Other examples include circle inversion, rotation by a half-turn, and reciprocal cipher
Reciprocal cipher
A reciprocal cipher means, just as one enters the plaintext into the cryptography system to get the ciphertext, one could enter the ciphertext into the same place in the system to get the plaintext. Sometimes also referred as self-reciprocal cipher....
s such as the ROT13
ROT13
ROT13 is a simple substitution cipher used in online forums as a means of hiding spoilers, punchlines, puzzle solutions, and offensive materials from the casual glance. ROT13 has been described as the "Usenet equivalent of a magazine printing the answer to a quiz upside down"...
transformation and the Beaufort
Beaufort cipher
The Beaufort cipher, created by Sir Francis Beaufort, is a substitution cipher that is similar to the Vigenère cipher but uses a slightly modified enciphering mechanism and tableau....
polyalphabetic cipher
Polyalphabetic cipher
A polyalphabetic cipher is any cipher based on substitution, using multiple substitution alphabets. The Vigenère cipher is probably the best-known example of a polyalphabetic cipher, though it is a simplified special case...
.
The number of involutions on a set with n = 0, 1, 2, … elements is given by the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
:
- a0 = a1 = 1;
- an = an − 1 + (n − 1)an − 2, for n > 1.
The first few terms of this sequence are 1, 1, 2, 4, 10
10 (number)
10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
, 26
26 (number)
26 is the natural number following 25 and preceding 27.- In mathematics :26 is the only positive integer that is one greater than a square and one less than a cube .A rhombicuboctahedron has twenty-six sides....
, 76
76 (number)
76 is the natural number following 75 and preceding 77.-In mathematics:Seventy-six is a Lucas number, an automorphic number, a nontotient, a 14-gonal number, and a centered pentagonal number....
, 232 .
Euclidean geometry
A simple example of an involution of the three-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
against a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
. Performing a reflection twice brings a point back to its original coordinates.
Another is the so-called reflection through the origin; this is an abuse of language, as it is actually an involution, not a reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
.
These transformations are examples of affine involution
Affine involution
In Euclidean geometry, of special interest are involutions which are linear or affine transformations over the Euclidean space Rn. Such involutions are easy to characterize and they can be described geometrically.-Linear involutions:...
s.
Linear algebra
In linear algebra, an involution is a linear operator T such that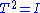 . Except for in characteristic 2, such operators are diagonalizable with 1s and −1s on the diagonal. If the operator is orthogonal (an orthogonal involution), it is orthonormally diagonalizable.
. Except for in characteristic 2, such operators are diagonalizable with 1s and −1s on the diagonal. If the operator is orthogonal (an orthogonal involution), it is orthonormally diagonalizable.The transpose of a square matrix is an involution because the transpose of the transpose of a matrix is itself.
Involutions are related to idempotents; if 2 is invertible, (in a field of characteristic other than 2), then they are equivalent.
Quaternion algebra
In a Quaternion algebraQuaternion algebra
In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
, an (anti-)involution is defined by the following axioms: if we consider a transformation
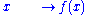 then an involution is
then an involution is
-
 . An involution is its own inverse
. An involution is its own inverse - An involution is linear:
 and
and 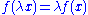
-
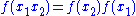
An anti-involution does not obey the last axiom but instead
Ring theory
In ring theoryRing theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, the word involution is customarily taken to mean an antihomomorphism
Antihomomorphism
In mathematics, an antihomomorphism is a type of function defined on sets with multiplication that reverses the order of multiplication. An antiautomorphism is an antihomomorphism which has an inverse as an antihomomorphism; this coincides with it being a bijection from an object to...
that is its own inverse function.
Examples of involutions in common rings:
- complex conjugation on the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
- multiplication by j in the split-complex numberSplit-complex numberIn abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s - taking the transposeTransposeIn linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
in a matrix ring.
Group theory
In group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, an element of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is an involution if it has order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
2; i.e. an involution is an element a such that a ≠ e and a2 = e, where e is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. Originally, this definition agreed with the first definition above, since members of groups were always bijections from a set into itself; i.e., group was taken to mean permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
. By the end of the 19th century, group was defined more broadly, and accordingly so was involution.
A permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
is an involution precisely if it can be written as a product of one or more non-overlapping transpositions.
The involutions of a group have a large impact on the group's structure. The study of involutions was instrumental in the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
.
Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s are groups generated by involutions with the relations determined only by relations given for pairs of the generating involutions. Coxeter groups can be used, among other things, to describe the possible regular polyhedra
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
and their generalizations to higher dimensions
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
.
Mathematical logic
The operation of complement in Boolean algebras is an involution. Accordingly, negationNegation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
in classical logic satisfies the law of double negation: ¬¬A is equivalent to A.
Generally in non-classical logics, negation which satisfies the law of double negation is called involutive. In algebraic semantics, such a negation is realized as an involution on the algebra of truth values. Examples of logics which have involutive negation are Kleene and Bochvar three-valued logics, Łukasiewicz many-valued logic, fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
IMTL, etc. Involutive negation is sometimes added as an additional connective to logics with non-involutive negation; this is usual, for example, in t-norm fuzzy logics
T-norm fuzzy logics
T-norm fuzzy logics are a family of non-classical logics, informally delimited by having a semantics which takes the real unit interval [0, 1] for the system of truth values and functions called t-norms for permissible interpretations of conjunction...
.
The involutiveness of negation is an important characterization property for logics and the corresponding varieties of algebras
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
. For instance, involutive negation characterizes Boolean algebras among Heyting algebra
Heyting algebra
In mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
s. Correspondingly, classical Boolean logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
arises by adding the law of double negation to intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
. The same relationship holds also between MV-algebra
MV-algebra
In abstract algebra, a branch of pure mathematics, an MV-algebra is an algebraic structure with a binary operation \oplus, a unary operation \neg, and the constant 0, satisfying certain axioms...
s and BL-algebras (and so correspondingly between Łukasiewicz logic and fuzzy logic BL
BL (logic)
Basic fuzzy Logic , the logic of continuous t-norms, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of all left-continuous t-norms MTL....
), IMTL and MTL
Monoidal t-norm logic
Monoidal t-norm based logic , the logic of left-continuous t-norms, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of commutative bounded integral residuated lattices by the axiom of...
, and other pairs of important varieties of algebras (resp. corresponding logics).
Computer science
The XOR bitwise operationBitwise operation
A bitwise operation operates on one or more bit patterns or binary numerals at the level of their individual bits. This is used directly at the digital hardware level as well as in microcode, machine code and certain kinds of high level languages...
is also an involution. XOR masks
Mask (computing)
In computer science, a mask is data that is used for bitwise operations.Using a mask, multiple bits in a byte, nibble, word can be set either on, off or inverted from on to off in a single bitwise operation.-Masking bits to 1:...
were once used to draw graphics on images in such a way that drawing them twice on the background reverts the background to its original state.