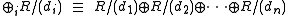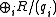Structure theorem for finitely generated modules over a principal ideal domain
Encyclopedia
In mathematics
, in the field of abstract algebra
, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in much the same way that integers have a prime factorization. The result provides a simple framework to understand various canonical form results for square matrices over fields.
F has a finite generating set, then one may extract from it a basis consisting of a finite number n of vectors, and the space is therefore isomorphic to Fn. The corresponding statement with the F generalized to a principal ideal domain
R is no longer true, as a finitely generated module over R need not have any basis. However such a module is still isomorphic to a quotient of some module Rn with n finite (to see this it suffices to construct the morphism that sends the elements of the canonical basis Rn to the generators of the module, and take the quotient by its kernel
. By changing the choice of generating set, one can in fact describe the module as the quotient of some Rn by a particularly simple submodule, and this is the structure theorem.
The structure theorem for finitely generated modules over a principal ideal domain
has two statements, which are equivalent by the Chinese remainder theorem
:
Some prefer to separate out the free part and write M as: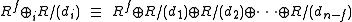
where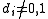
and 
.
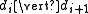The free part is where (in the first formulation)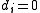
; these occur at the end, as everything divides zero.
Note that in a PID, primary ideals are powers of primes, so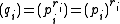
.
The summands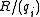
are indecomposable
, so the primary decomposition is a decomposition into indecomposable modules, and thus every finitely generated module over a PID is completely decomposable.
Some prefer to separate out the free part (where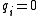
) and write M as: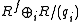
where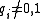
and the 
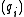are primary ideal
s.
This yields the invariant factor decomposition, and the diagonal entries of Smith normal form are the invariant factors.
Another outline of a proof:
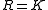. Since fields have no non-trivial ideals, every finitely generated vector space is free.
Taking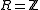
yields the fundamental theorem of finitely generated abelian groups.
Taking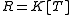
classifies linear operators on a finite-dimensional vector space – an operator on a vector space is the same as an algebra representation of the polynomial algebra in one variable – where the last invariant factor is the minimal polynomial, and the product of invariant factors is the characteristic polynomial
. Combined with a standard matrix form for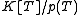
, this yields various canonical form
s:
is not unique, and does not even preserve the direct sum
decomposition. This follows because there are non-trivial automorphisms of these modules which do not preserve the summands.
However, one has a canonical torsion submodule T, and similar canonical submodules corresponding to each (distinct) invariant factor, which yield a canonical sequence: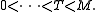
Compare composition series
in Jordan–Hölder theorem.
For instance, if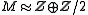
, and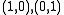 
is one basis, then
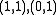is another basis, and the change of basis matrix 
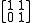does not preserve the summand 
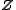. However, it does preserve the 
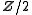summand, as this is the torsion submodule (equivalently here, the 2-torsion elements).
, rather than a direct sum
.
The Krull–Schmidt theorem
and related results give conditions under which a module has something like a primary decomposition, a decomposition as a direct sum of indecomposable module
s in which the summands are unique up to order.
s, and this result is called the Lasker–Noether theorem
.
, which vanishes for PIDs.
For rings that are not principal ideal domains, unique decomposition need not even hold for modules over a ring generated by two elements. For the ring R = Z[√−5], both the module R and its submodule M generated by 2 and 1 + √−5 are indecomposable. While R is not isomorphic to M, R ⊕ R is isomorphic to M ⊕ M; thus the images of the M summands give indecomposable submodules L1, L2 < R ⊕ R which give a different decomposition of R ⊕ R. The failure of uniquely factorizing R ⊕ R into a direct sum of indecomposable modules is directly related (via the ideal class group) to the failure of the unique factorization of elements of R into irreducible elements of R.
Another issue that arises with non-finitely generated modules is that there are torsion-free modules which are not free. For instance, consider the ring Z of integers. A classical example of a torsion-free module which is not free is the Baer–Specker group
, the group of all sequences of integers under termwise addition. In general, the question of which infinitely generated torsion-free abelian groups are free depends on which large cardinals exist. A consequence is that any structure theorem for infinitely generated modules depends on a choice of set theory axioms and may be invalid under a different choice.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in much the same way that integers have a prime factorization. The result provides a simple framework to understand various canonical form results for square matrices over fields.
Statement
When a vector space over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F has a finite generating set, then one may extract from it a basis consisting of a finite number n of vectors, and the space is therefore isomorphic to Fn. The corresponding statement with the F generalized to a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
R is no longer true, as a finitely generated module over R need not have any basis. However such a module is still isomorphic to a quotient of some module Rn with n finite (to see this it suffices to construct the morphism that sends the elements of the canonical basis Rn to the generators of the module, and take the quotient by its kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
. By changing the choice of generating set, one can in fact describe the module as the quotient of some Rn by a particularly simple submodule, and this is the structure theorem.
The structure theorem for finitely generated modules over a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
has two statements, which are equivalent by the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
:
Invariant factor decomposition
- Every finitely generated module M over a principal ideal domain R is isomorphic to a unique one of the form
- where
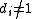and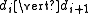 
. - The elements
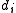(up to unit) are a complete set of invariantsComplete set of invariantsIn mathematics, a complete set of invariants for a classification problem is a collection of mapsf_i : X \to Y_i \,, such that x ∼ x' if and only if f_i = f_i for all i...
for finitely generated R-modules, and are called invariant factorInvariant factorThe invariant factors of a module over a principal ideal domain occur in one form of the structure theorem for finitely generated modules over a principal ideal domain.If R is a PID and M a finitely generated R-module, then...
s. - The ideals
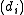are unique; the elements 
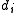are unique up to multiplication by a unitUnit (ring theory)In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
, but the order is unique.
Some prefer to separate out the free part and write M as:
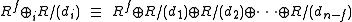
where
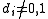and 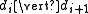.The free part is where (in the first formulation)
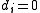; these occur at the end, as everything divides zero.Primary decomposition
- Every finitely generated module M over a principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
R is isomorphic to a unique one of the form - where
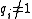and the 
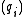are primary idealPrimary idealIn mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
s. The ideals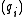
are unique (up to order); the elements 
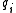are unique up to multiplication by a unitUnit (ring theory)In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
, and are called the elementary divisors.
Note that in a PID, primary ideals are powers of primes, so
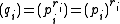.The summands
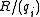are indecomposableIndecomposable module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
, so the primary decomposition is a decomposition into indecomposable modules, and thus every finitely generated module over a PID is completely decomposable.
Some prefer to separate out the free part (where
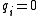) and write M as: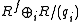where
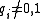and the 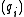are primary idealPrimary ideal
In mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
s.
Proofs
One proof proceeds as follows:- Every finitely generated module over a PID is also finitely presented because a PID is NoetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
, an even stronger condition than coherenceCoherent ringIn mathematics, a coherent ring is a ring in which every finitely generated left ideal is finitely presented.Many theorems about finitely generated modules over Noetherian rings can be extended to finitely presented modules over coherent rings....
. - Take a presentation, which is a map
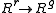(relations to generators), and put it in Smith normal formSmith normal formIn mathematics, the Smith normal form is a normal form that can be defined for any matrix with entries in a principal ideal domain . The Smith normal form of a matrix is diagonal, and can be obtained from the original matrix by multiplying on the left and right by invertible square matrices...
.
This yields the invariant factor decomposition, and the diagonal entries of Smith normal form are the invariant factors.
Another outline of a proof:
- Denote by tM the torsion submodule of M. Then M/tM is a finitely generatedFinitely generatedIn mathematics, finitely generated may refer to:* Finitely generated group* Finitely generated monoid* Finitely generated abelian group* Finitely generated module* Finitely generated ideal* Finitely generated algebra* Finitely generated space...
torsion free module, and such a module over a commutative PID is a free moduleFree moduleIn mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
of finite rank. As a result,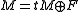
where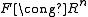 
for a positive integer n. - For a prime p in R we can then speak of
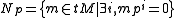for each prime p. This is a submodule of tM, and it turns out that each Np is a direct sum of cyclic modules, and that tM is a direct sum of Np for a finite number of distinct primes p. - Putting the previous two steps together, M is decomposed into cyclic modules of the indicated types.
Corollaries
This includes the classification of finite-dimensional vector spaces as a special case, where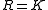. Since fields have no non-trivial ideals, every finitely generated vector space is free.Taking
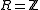yields the fundamental theorem of finitely generated abelian groups.Taking
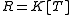classifies linear operators on a finite-dimensional vector space – an operator on a vector space is the same as an algebra representation of the polynomial algebra in one variable – where the last invariant factor is the minimal polynomial, and the product of invariant factors is the characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
. Combined with a standard matrix form for
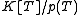, this yields various canonical formCanonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
s:
- invariant factors + companion matrix yields Frobenius normal formFrobenius normal formIn linear algebra, the Frobenius normal form, Turner binormal projective form or rational canonical form of a square matrix A is a canonical form for matrices that reflects the structure of the minimal polynomial of A and provides a means of detecting whether another matrix B is similar to A...
(aka, rational canonical form) - primary decomposition + companion matrix yields primary rational canonical form
- primary decomposition + Jordan blocks yields Jordan canonical form (this latter only holds over an algebraically closed fieldAlgebraically closed fieldIn mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
)
Uniqueness
While the invariants (rank, invariant factors, and elementary divisors) are unique, the isomorphism between M and its canonical formCanonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
is not unique, and does not even preserve the direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
decomposition. This follows because there are non-trivial automorphisms of these modules which do not preserve the summands.
However, one has a canonical torsion submodule T, and similar canonical submodules corresponding to each (distinct) invariant factor, which yield a canonical sequence:
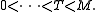
Compare composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
in Jordan–Hölder theorem.
For instance, if
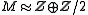, and 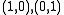is one basis, then 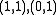is another basis, and the change of basis matrix 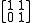does not preserve the summand 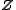. However, it does preserve the 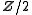summand, as this is the torsion submodule (equivalently here, the 2-torsion elements).Groups
The Jordan–Hölder theorem is a more general result for finite groups (or modules over an arbitrary ring). In this generality, one obtains a composition seriesComposition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
, rather than a direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
.
The Krull–Schmidt theorem
Krull–Schmidt theorem
In mathematics, the Krull–Schmidt theorem states that a group subjected to certain finiteness conditions on chains of subgroups, can be uniquely written as a finite direct product of indecomposable subgroups.-Definitions:...
and related results give conditions under which a module has something like a primary decomposition, a decomposition as a direct sum of indecomposable module
Indecomposable module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
s in which the summands are unique up to order.
Primary decomposition
The primary decomposition generalizes to finitely generated modules over commutative Noetherian ringNoetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
s, and this result is called the Lasker–Noether theorem
Lasker–Noether theorem
In mathematics, the Lasker–Noether theorem states that every Noetherian ring is a Lasker ring, which means that every ideal can be written as an intersection of finitely many primary ideals...
.
Indecomposable modules
By contrast, unique decomposition into indecomposable submodules does not generalize as far, and the failure is measured by the ideal class groupIdeal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
, which vanishes for PIDs.
For rings that are not principal ideal domains, unique decomposition need not even hold for modules over a ring generated by two elements. For the ring R = Z[√−5], both the module R and its submodule M generated by 2 and 1 + √−5 are indecomposable. While R is not isomorphic to M, R ⊕ R is isomorphic to M ⊕ M; thus the images of the M summands give indecomposable submodules L1, L2 < R ⊕ R which give a different decomposition of R ⊕ R. The failure of uniquely factorizing R ⊕ R into a direct sum of indecomposable modules is directly related (via the ideal class group) to the failure of the unique factorization of elements of R into irreducible elements of R.
Non-finitely generated modules
Similarly for modules that are not finitely generated, one cannot expect such a nice decomposition: even the number of factors may vary. There are Z-submodules A of Q4 which are simultaneously direct sums of two indecomposable modules and direct sums of three indecomposable modules, showing the analogue of the primary decomposition cannot hold for infinitely generated modules, even over the integers, Z.Another issue that arises with non-finitely generated modules is that there are torsion-free modules which are not free. For instance, consider the ring Z of integers. A classical example of a torsion-free module which is not free is the Baer–Specker group
Baer–Specker group
In mathematics, in the field of group theory, the Baer–Specker group, or Specker group, is an example of an infinite Abelian group which is a building block in the structure theory of such groups.-Definition:...
, the group of all sequences of integers under termwise addition. In general, the question of which infinitely generated torsion-free abelian groups are free depends on which large cardinals exist. A consequence is that any structure theorem for infinitely generated modules depends on a choice of set theory axioms and may be invalid under a different choice.