
Krull–Schmidt theorem
Encyclopedia
In mathematics
, the Krull–Schmidt theorem states that a group
subjected to certain finiteness conditions on chains of subgroup
s, can be uniquely written as a finite direct product
of indecomposable subgroups.
(ACC) on subgroups if every sequence
of subgroups of G:

is eventually constant, i.e., there exists N such that GN = GN+1 = GN+2 = ... . We say that G satisfies the ACC on normal subgroups if every such sequence of normal subgroups of G eventually becomes constant.
Likewise, one can define the descending chain condition on (normal) subgroups, by looking at all decreasing sequences of (normal) subgroups:
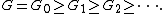
Clearly, all finite groups satisfy both ACC and DCC on subgroups. The infinite cyclic group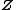 satisfies ACC but not DCC, since (2) > (2)2 > (2)3 > ... is an infinite decreasing sequence of subgroups. On the other hand, the
satisfies ACC but not DCC, since (2) > (2)2 > (2)3 > ... is an infinite decreasing sequence of subgroups. On the other hand, the 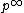 -torsion part of
-torsion part of  (the quasicyclic p-group
(the quasicyclic p-group
) satisfies DCC but not ACC.
We say a group G is indecomposable if it cannot be written as a direct product of non-trivial subgroups G = H × K.
If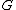 is a group that satisfies ACC and DCC on normal subgroups, then there is a unique way of writing
is a group that satisfies ACC and DCC on normal subgroups, then there is a unique way of writing 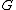 as a direct product
as a direct product  of finitely many indecomposable subgroups of
of finitely many indecomposable subgroups of  . Here, uniqueness means direct decompositions into indecomposable subgroups have the exchange property. That is: suppose
. Here, uniqueness means direct decompositions into indecomposable subgroups have the exchange property. That is: suppose  is another expression of
is another expression of  as a product of indecomposable subgroups. Then
as a product of indecomposable subgroups. Then 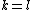 and there is a reindexing of the
and there is a reindexing of the 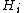 's satisfying
's satisfying
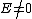 is a module
is a module
that satisfies the ACC and DCC on submodules (that is, it is both Noetherian
and Artinian
or – equivalently – of finite length
), then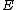 is a direct sum
is a direct sum
of indecomposable module
s. Up to a permutation, the indecomposable components in such a direct sum are uniquely determined up to isomorphism.
In general, the theorem fails, if one only assumes that the module is Noetherian.
(Ann. of Math (1909)), for finite groups, though he mentions some credit is due to an earlier study of G.A. Miller
where direct products of abelian groups were considered. Wedderburn's theorem is stated as an exchange property between direct decompositions of maximum length. However, Wedderburn's proof makes no use of automorphisms.
The thesis of Robert Remak
(1911) derived the same uniqueness result as Wedderburn but also proved (in modern terminology) that the group of central automorphisms acts transitively on the set of direct decompositions of maximum length of a finite group. From that stronger theorem Remak also proved various corollaries including that groups with a trivial center and perfect groups have a unique Remak decomposition.
Otto Schmidt
(Sur les produits directs, S. M. F. Bull. 41 (1913), 161–164), simplified the main theorems of Remak to the 3 page predecessor to today's textbook proofs. His method improves Remak's use of idempotents to create the appropriate central automorphisms. Both Remak and Schmidt published subsequent proofs and corollaries to their theorems.
Wolfgang Krull
(Über verallgemeinerte endliche Abelsche Gruppen, M. Z. 23 (1925) 161–196), returned to G.A. Miller
's original problem of direct products of abelian groups by extending to abelian operator groups with ascending and descending chain conditions. This is most often stated in the language of modules. His proof observes that the idempotents used in the proofs of Remak and Schmidt can be restricted to module homomorphisms; the remaining details of the proof are largely unchanged.
O. Ore unified the proofs from various categories include finite groups, abelian operator groups, rings and algebras by proving the exchange theorem of Wedderburn holds for modular lattices with descending and ascending chain conditions. This proof makes no use of idempotents and does not reprove the transitivity of Remak's theorems.
Kurosh's The Theory of Groups and Zassenhaus' The Theory of Groups include the proofs of Schmidt and Ore under the name of Remak–Schmidt but acknowledge Wedderburn and Ore. Later texts use the title Krull–Schmidt (Hungerford
's Algebra) and Krull–Schmidt–Azumaya
(Curtis–Reiner). The name Krull–Schmidt is now popularly substituted for any theorem concerning uniqueness of direct products of maximum size. Some authors choose to call direct decompositions of maximum-size Remak decompositions to honor his contributions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Krull–Schmidt theorem states that a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
subjected to certain finiteness conditions on chains of subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s, can be uniquely written as a finite direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of indecomposable subgroups.
Definitions
We say that a group G satisfies the ascending chain conditionAscending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
(ACC) on subgroups if every sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of subgroups of G:

is eventually constant, i.e., there exists N such that GN = GN+1 = GN+2 = ... . We say that G satisfies the ACC on normal subgroups if every such sequence of normal subgroups of G eventually becomes constant.
Likewise, one can define the descending chain condition on (normal) subgroups, by looking at all decreasing sequences of (normal) subgroups:
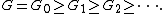
Clearly, all finite groups satisfy both ACC and DCC on subgroups. The infinite cyclic group
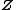 satisfies ACC but not DCC, since (2) > (2)2 > (2)3 > ... is an infinite decreasing sequence of subgroups. On the other hand, the
satisfies ACC but not DCC, since (2) > (2)2 > (2)3 > ... is an infinite decreasing sequence of subgroups. On the other hand, the 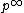 -torsion part of
-torsion part of  (the quasicyclic p-group
(the quasicyclic p-groupPrüfer group
In mathematics, specifically in group theory, the Prüfer p-group or the p-quasicyclic group or p∞-group, Z, for a prime number p is the unique p-group in which every element has p pth roots. The group is named after Heinz Prüfer...
) satisfies DCC but not ACC.
We say a group G is indecomposable if it cannot be written as a direct product of non-trivial subgroups G = H × K.
Krull–Schmidt theorem
The theorem says:If
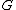 is a group that satisfies ACC and DCC on normal subgroups, then there is a unique way of writing
is a group that satisfies ACC and DCC on normal subgroups, then there is a unique way of writing 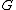 as a direct product
as a direct product  of finitely many indecomposable subgroups of
of finitely many indecomposable subgroups of  . Here, uniqueness means direct decompositions into indecomposable subgroups have the exchange property. That is: suppose
. Here, uniqueness means direct decompositions into indecomposable subgroups have the exchange property. That is: suppose  is another expression of
is another expression of  as a product of indecomposable subgroups. Then
as a product of indecomposable subgroups. Then 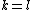 and there is a reindexing of the
and there is a reindexing of the 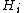 's satisfying
's satisfying-
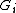 and
and 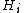 are isomorphic for each
are isomorphic for each  ;
; -
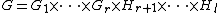 for each
for each  .
.
Krull–Schmidt theorem for modules
If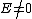 is a module
is a moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
that satisfies the ACC and DCC on submodules (that is, it is both Noetherian
Noetherian module
In abstract algebra, an Noetherian module is a module that satisfies the ascending chain condition on its submodules, where the submodules are partially ordered by inclusion....
and Artinian
Artinian module
In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
or – equivalently – of finite length
Length of a module
In abstract algebra, the length of a module is a measure of the module's "size". It is defined to be the length of the longest chain of submodules and is a generalization of the concept of dimension for vector spaces...
), then
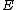 is a direct sum
is a direct sumDirect sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of indecomposable module
Indecomposable module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
s. Up to a permutation, the indecomposable components in such a direct sum are uniquely determined up to isomorphism.
In general, the theorem fails, if one only assumes that the module is Noetherian.
History
The present-day Krull–Schmidt theorem was first proved by Joseph WedderburnJoseph Wedderburn
Joseph Henry Maclagan Wedderburn was a Scottish mathematician, who taught at Princeton University for most of his career. A significant algebraist, he proved that a finite division algebra is a field, and part of the Artin–Wedderburn theorem on simple algebras...
(Ann. of Math (1909)), for finite groups, though he mentions some credit is due to an earlier study of G.A. Miller
George Abram Miller
George Abram Miller was an early group theorist whose many papers and texts were considered important by his contemporaries, but are now mostly considered only of historical importance...
where direct products of abelian groups were considered. Wedderburn's theorem is stated as an exchange property between direct decompositions of maximum length. However, Wedderburn's proof makes no use of automorphisms.
The thesis of Robert Remak
Robert Remak (mathematician)
Robert Erich Remak was a German mathematician. He is chiefly remembered for his work in group theory . His other interests included algebraic number theory, mathematical economics and geometry of numbers...
(1911) derived the same uniqueness result as Wedderburn but also proved (in modern terminology) that the group of central automorphisms acts transitively on the set of direct decompositions of maximum length of a finite group. From that stronger theorem Remak also proved various corollaries including that groups with a trivial center and perfect groups have a unique Remak decomposition.
Otto Schmidt
Otto Schmidt
Otto Yulyevich Schmidt was a Soviet scientist, mathematician, astronomer, geophysicist, statesman, academician, Hero of the USSR , and member of the Communist Party.-Biography:He was born in Mogilev, Russian Empire...
(Sur les produits directs, S. M. F. Bull. 41 (1913), 161–164), simplified the main theorems of Remak to the 3 page predecessor to today's textbook proofs. His method improves Remak's use of idempotents to create the appropriate central automorphisms. Both Remak and Schmidt published subsequent proofs and corollaries to their theorems.
Wolfgang Krull
Wolfgang Krull
Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...
(Über verallgemeinerte endliche Abelsche Gruppen, M. Z. 23 (1925) 161–196), returned to G.A. Miller
George Abram Miller
George Abram Miller was an early group theorist whose many papers and texts were considered important by his contemporaries, but are now mostly considered only of historical importance...
's original problem of direct products of abelian groups by extending to abelian operator groups with ascending and descending chain conditions. This is most often stated in the language of modules. His proof observes that the idempotents used in the proofs of Remak and Schmidt can be restricted to module homomorphisms; the remaining details of the proof are largely unchanged.
O. Ore unified the proofs from various categories include finite groups, abelian operator groups, rings and algebras by proving the exchange theorem of Wedderburn holds for modular lattices with descending and ascending chain conditions. This proof makes no use of idempotents and does not reprove the transitivity of Remak's theorems.
Kurosh's The Theory of Groups and Zassenhaus' The Theory of Groups include the proofs of Schmidt and Ore under the name of Remak–Schmidt but acknowledge Wedderburn and Ore. Later texts use the title Krull–Schmidt (Hungerford
Thomas W. Hungerford
Thomas William Hungerford is an American mathematician who works in algebra and mathematics education. He is the author or coauthor of several widely used and widely cited textbooks covering high-school to graduate-level mathematics. From 1963 until 1980 he taught at the University of Washington...
's Algebra) and Krull–Schmidt–Azumaya
Goro Azumaya
was a Japanese mathematician who introduced the notion of Azumaya algebra in 1951. His advisor was Shokichi Iyanaga. At the time of his death he was an emeritus professor at Indiana University.-External links:...
(Curtis–Reiner). The name Krull–Schmidt is now popularly substituted for any theorem concerning uniqueness of direct products of maximum size. Some authors choose to call direct decompositions of maximum-size Remak decompositions to honor his contributions.
Further reading
- Hungerford, Thomas W. Algebra, Graduate Texts in Mathematics Volume 73. ISBN 0-387-90518-9
- A. Facchini: Module theory. Endomorphism rings and direct sum decompositions in some classes of modules. Progress in Mathematics, 167. Birkhäuser Verlag, Basel, 1998. ISBN 3-7643-5908-0
- A. Facchini, D. Herbera, L.S. Levy, P. Vámos: Krull–Schmidt fails for Artinian modules. Proc. Amer. Math. Soc. 123 (1995), no. 12, 3587–3592.
- C.M. Ringel: Krull–Remak–Schmidt fails for Artinian modules over local rings. Algebr. Represent. Theory 4 (2001), no. 1, 77–86.

