
Composition series
Encyclopedia
In abstract algebra
, a composition series provides a way to break up an algebraic structure, such as a group
or a module
, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple
, hence cannot be decomposed into a direct sum
of simple module
s. A composition series of a module M is a finite increasing filtration
of M by submodules such that the successive quotients are simple and serves as a replacement of the direct sum decomposition of M into its simple constituents.
A composition series may not even exist, and when it does, it need not be unique. Nevertheless, a group of results known under the general name Jordan-Hölder theorem asserts that whenever composition series exist, the isomorphism class
es of simple pieces (although, perhaps, not their location in the composition series in question) and their multiplicities are uniquely determined. Composition series may thus be used to define invariants of finite group
s and Artinian module
s.
A related but distinct concept is a chief series
: a composition series is a maximal subnormal series, while a chief series is a maximal normal series
.
N, then the factor group G/N may be formed, and some aspects of the study of the structure of G may be broken down by studying the "smaller" groups G/N and N. If G has no normal subgroup that is different from G and from the trivial group, then G is a simple group
. Otherwise, the question naturally arises as to whether G can be reduced to simple "pieces", and if so, are there any unique features of the way this can be done?
More formally, a composition series of a group
G is a subnormal series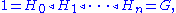
with strict inclusions, such that each Hi is a maximal
normal subgroup of Hi+1. Equivalently, a composition series is a subnormal series such that each factor group Hi+1 / Hi is simple
. The factor groups are called composition factors.
A subnormal series is a composition series if and only if
it is of maximal length. That is, there are no additional subgroups which can be "inserted" into a composition series. The length n of the series is called the composition length.
If a composition series exists for a group G, then any subnormal series of G can be refined to a composition series, informally, by inserting subgroups into the series up to maximality. Every finite group
has a composition series, but not every infinite group
has one. For example, the infinite cyclic group
has no composition series.
and Otto Hölder
) states that any two composition series of a given group are equivalent. That is, they have the same composition length and the same composition factors, up to
permutation
and isomorphism
. This theorem can be proved using the Schreier refinement theorem
. The Jordan–Hölder theorem is also true for transfinite ascending composition series, but not transfinite descending composition series .
Transfinite ascending composition series are related to the concept of hypertranssimplicity . A group is called hypertranssimple if it has no
ascending subnormal series (neither finite nor transfinite ) other than the trivial series of the length one.
.
For example, the cyclic group C12 has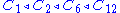 ,
,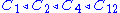 ,
,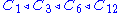
as different composition series.
The sequences of composition factors obtained in the respective cases are
for M is a series of submodules

where all inclusions are strict and Jk is a maximal submodule of Jk+1 for each k. As for groups, if M has a composition series at all, then any finite strictly increasing series of submodules of M may be refined to a composition series, and any two composition series for M are equivalent. In that case, the (simple) quotient modules Jk+1/Jk are known as the composition factors of M, and the number of occurrences of each isomorphism type of simple R-module as a composition factor does not depend on the choice of composition series. If R is an Artinian ring
, then every finitely generated R-module has a composition series by the Hopkins-Levitzki theorem. In particular, for any field K, any finite-dimensional module for a finite-dimensional algebra over K has a composition series, unique up to equivalence.
A middle ground between modules and groups is the concept of groups with a set of operators
. Restricting attention to subgroups invariant under the action of the operators, nearly identical proofs establish the corresponding results, such as the Jordan-Hölder theorem. An important case occurs where the set of operators is the set of inner automorphism
s, then the corresponding idea of a composition series is instead a chief series
. A unified approach to both groups and modules can be followed, simplifying some of the exposition .
is a sequence of subobjects
such that each quotient object Xi /Xi + 1 is simple (for ). If A has a composition series, the integer n only depends on A and is called the length of A.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a composition series provides a way to break up an algebraic structure, such as a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
or a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple
Semisimple module
In mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
, hence cannot be decomposed into a direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of simple module
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
s. A composition series of a module M is a finite increasing filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
of M by submodules such that the successive quotients are simple and serves as a replacement of the direct sum decomposition of M into its simple constituents.
A composition series may not even exist, and when it does, it need not be unique. Nevertheless, a group of results known under the general name Jordan-Hölder theorem asserts that whenever composition series exist, the isomorphism class
Isomorphism class
An isomorphism class is a collection of mathematical objects isomorphic to each other.Isomorphism classes are often defined if the exact identity of the elements of the set is considered irrelevant, and the properties of the structure of the mathematical object are studied. Examples of this are...
es of simple pieces (although, perhaps, not their location in the composition series in question) and their multiplicities are uniquely determined. Composition series may thus be used to define invariants of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s and Artinian module
Artinian module
In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
s.
A related but distinct concept is a chief series
Chief series
In abstract algebra, a chief series is a maximal normal series for a group.It is similar to a composition series, though the two concepts are distinct in general: a chief series is a maximal normal series, while a composition series is a maximal subnormal series.Chief series can be thought of as...
: a composition series is a maximal subnormal series, while a chief series is a maximal normal series
Normal series
In mathematics, a subgroup series is a chain of subgroups:1 = A_0 \leq A_1 \leq \cdots \leq A_n = G.Subgroup series can simplify the study of a group to the study of simpler subgroups and their relations, and several subgroup series can be invariantly defined and are important invariants of groups...
.
For groups
If a group G has a normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
N, then the factor group G/N may be formed, and some aspects of the study of the structure of G may be broken down by studying the "smaller" groups G/N and N. If G has no normal subgroup that is different from G and from the trivial group, then G is a simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
. Otherwise, the question naturally arises as to whether G can be reduced to simple "pieces", and if so, are there any unique features of the way this can be done?
More formally, a composition series of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is a subnormal series
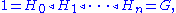
with strict inclusions, such that each Hi is a maximal
Maximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
normal subgroup of Hi+1. Equivalently, a composition series is a subnormal series such that each factor group Hi+1 / Hi is simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
. The factor groups are called composition factors.
A subnormal series is a composition series if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is of maximal length. That is, there are no additional subgroups which can be "inserted" into a composition series. The length n of the series is called the composition length.
If a composition series exists for a group G, then any subnormal series of G can be refined to a composition series, informally, by inserting subgroups into the series up to maximality. Every finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
has a composition series, but not every infinite group
Infinite group
In group theory, an area of mathematics, an infinite group is a group, of which the underlying set contains an infinite number of elements....
has one. For example, the infinite cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
has no composition series.
Uniqueness: Jordan–Hölder theorem
A group may have more than one composition series. However, the Jordan–Hölder theorem (named after Camille JordanCamille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
and Otto Hölder
Otto Hölder
Otto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...
) states that any two composition series of a given group are equivalent. That is, they have the same composition length and the same composition factors, up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
and isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. This theorem can be proved using the Schreier refinement theorem
Schreier refinement theorem
In mathematics, the Schreier refinement theorem of group theory states that any two normal series of subgroups of a given group have equivalent refinements....
. The Jordan–Hölder theorem is also true for transfinite ascending composition series, but not transfinite descending composition series .
Transfinite ascending composition series are related to the concept of hypertranssimplicity . A group is called hypertranssimple if it has no
ascending subnormal series (neither finite nor transfinite ) other than the trivial series of the length one.
Example
For a cyclic group of order n, composition series correspond to ordered prime factorizations of n, and in fact yields a proof of the fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
.
For example, the cyclic group C12 has
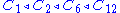 ,
,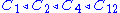 ,
,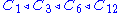
as different composition series.
The sequences of composition factors obtained in the respective cases are
-
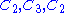
-
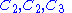 and
and -
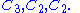
For modules
Given a ring R and an R-module M, a composition seriesfor M is a series of submodules

where all inclusions are strict and Jk is a maximal submodule of Jk+1 for each k. As for groups, if M has a composition series at all, then any finite strictly increasing series of submodules of M may be refined to a composition series, and any two composition series for M are equivalent. In that case, the (simple) quotient modules Jk+1/Jk are known as the composition factors of M, and the number of occurrences of each isomorphism type of simple R-module as a composition factor does not depend on the choice of composition series. If R is an Artinian ring
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
, then every finitely generated R-module has a composition series by the Hopkins-Levitzki theorem. In particular, for any field K, any finite-dimensional module for a finite-dimensional algebra over K has a composition series, unique up to equivalence.
A middle ground between modules and groups is the concept of groups with a set of operators
Group with operators
In abstract algebra, a branch of pure mathematics, the algebraic structure group with operators or Ω-group is a group with a set of group endomorphisms.Groups with operators were extensively studied by Emmy Noether and her school in the 1920s...
. Restricting attention to subgroups invariant under the action of the operators, nearly identical proofs establish the corresponding results, such as the Jordan-Hölder theorem. An important case occurs where the set of operators is the set of inner automorphism
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
s, then the corresponding idea of a composition series is instead a chief series
Chief series
In abstract algebra, a chief series is a maximal normal series for a group.It is similar to a composition series, though the two concepts are distinct in general: a chief series is a maximal normal series, while a composition series is a maximal subnormal series.Chief series can be thought of as...
. A unified approach to both groups and modules can be followed, simplifying some of the exposition .
For objects in an abelian category
A composition series of an object A in an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
is a sequence of subobjects

such that each quotient object Xi /Xi + 1 is simple (for ). If A has a composition series, the integer n only depends on A and is called the length of A.

