Structure tensor
Encyclopedia
In mathematics, the structure tensor
, also referred to as the second-moment matrix, is a matrix
derived from the gradient
of a function
. It summarizes the predominant directions of the gradient in a specified neighborhood of a point, and the degree to which those directions are coherent. The structure tensor is often used in image processing
and computer vision
.
of two variables p=(x,y), the structure tensor is the 2×2 matrix
where
and 
are the partial derivative
s of
with respect to x and y; the integrals range over the plane 
; and w is some fixed "window function", a distribution
on two variables. Note that the matrix Sw is itself a function of p=(x,y).
The formula above can be written also as
, where 
is the matrix-valued function defined by
If the gradient
of 
is viewed as a 1×2 (single-row) matrix, the matrix 
can be written as the matrix product 
, where 
denotes the 2×1 (single-column) transpose
of the gradient. (Note however that the structure tensor
cannot be factored in this way.)
is usually given as a discrete array of samples 
, where p is a pair of integer indices. The 2D structure tensor at a given pixel
is usually taken to be the discrete sum
Here the summation index r ranges over a finite set of index pairs (the "window", typically
for some m), and w[r] is a fixed "window weight" that depends on r, such that the sum of all weights is 1. The values 
are the partial derivatives sampled at pixel p; which, for instance, may be estimated from by 
by finite difference
formulas.
The formula of the structure tensor can be written also as
, where 
is the matrix-valued array such that
stems from the fact that its eigenvalues 
(which can be ordered so that 
) and the corresponding eigenvectors 
summarize the distribution of the gradient
of 
within the window defined by 
centered at 
.
Namely, if
, then 
(or 
) is the direction that is maximally aligned with the gradient within the window. In particular, if 
then the gradient is always a multiple of 
(positive, negative or zero); this is the case if and only if 
within the window varies along the direction 
but is constant along 
.
If
, on the other hand, the gradient in the window has no predominant direction; which happens, for instance, when the image has rotational symmetry
within that window. In particular,
if and only if the function 
is constant (
) within 
.
More generally, the value of
, for k=1 or k=2, is the 
-weighted average, in the neighborhood of p, of the square of the directional derivative
of
along 
. The relative discrepancy between the two eigenvalues of 
is an indicator of the degree of anisotropy
of the gradient in the window, namely how strongly is its biased towards a particular direction (and its opposite). This attribute can be quantified by the coherence, defined as
if
. This quantity is 1 when the gradient is totally aligned, and 0 when it has no preferred direction. The formula is undefined, even in the limit
, when the image is constant in the window (
). Some authors define it as 0 in that case.
Note that the average of the gradient
inside the window is not a good indicator of anisotropy. Aligned but oppositely oriented gradient vectors would cancel out in this average, whereas in the structure tensor they are properly added together.
By expanding the effective radius of the window function
(that is, increasing its variance), one can make the structure tensor more robust in the face of noise, at the cost of diminished spatial resolution. The formal basis for this property is described in more detail below, where it is shown that a multi-scale formulation of the structure tensor, referred to as the multi-scale structure tensor, constitutes a true multi-scale representation of directional data under variations of the spatial extent of the window function.
of three variables p=(x,y,z) in an entirely analogous way. Namely, in the continuous version we have 
, where
where
are the three partial derivatives of 
, and the integral ranges over 
. In the discrete version,
, where
and the sum ranges over a finite set of 3D indices, usually
for some m.
of 
, and the corresponding eigenvectors 
, summarize the distribution of gradient directions within the neighborhood of p defined by the window 
. This information can be visualized as an ellipsoid whose semi-axes are equal to the eigenvalues and directed along their corresponding eigenvectors.
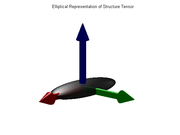In particular, if the ellipsoid is stretched along one axis only, like a cigar (that is, if 
is much larger than both 
and 
), it means that the gradient in the window is predominantly aligned with the direction 
, so that the isosurface
s of
tend to be flat and perpendicular to that vector. This situation occurs, for instance, when p lies on a thin plate-like feature, or on the smooth boundary between two regions with contrasting values.
If the ellipsoid is flattened in one direction only, like a pancake (that is, if
is much smaller than both 
and 
), it means that the gradient directions are spread out but perpendicular to 
; so that the isosurfaces tend to be like tubes parallel to that vector. This situation occurs, for instance, when p lies on a thin line-like feature, or on a sharp corner of the boundary between two regions with contrasting values.
Finally, if the ellipsoid is roughly spherical (that is, if
), it means that the gradient directions in the window are more or less evenly distributed, with no marked preference; so that the function 
is mostly isotropic in that neighborhood. This happens, for instance, when the function has spherical symmetry in the neighborhood of p. In particular, if the ellipsoid degenerates to a point (that is, if the three eigenvalues are zero), it means that 
is constant (has zero gradient) within the window.
is in contrast to other one-parameter scale-space features an image descriptor that is defined over two scale parameters.
One scale parameter, referred to as local scale
, is needed for determining the amount of pre-smoothing when computing the image gradient 
. Another scale parameter, referred to as integration scale 
, is needed for specifying the spatial extent of the window function 
that determines the weights for the region in space over which the components of the outer product of the gradient by itself 
are accumulated.
More precisely, suppose that
is a real-valued signal defined over 
. For any local scale 
, let a multi-scale representation 
of this signal be given by 
where 
represents a pre-smoothing kernel. Furthermore, let 
denote the gradient of the scale-space representation.
Then, the multi-scale structure tensor/second-moment matrix is defined by
Conceptually, one may ask if it would be sufficient to use any self-similar families of smoothing functions
and 
. If one naively would apply, for example, a box filter, however, then non-desirable artifacts could easily occur. If one wants the multi-scale structure tensor to be well-behaved over both increasing local scales 
and increasing integration scales 
, then it can be shown that both the smoothing function and the window function have to be Gaussian. The conditions that specifify this uniqueness are similar to the scale-space axioms
that are used for deriving the uniqueness of the Gaussian kernel for a regular Gaussian scale-space of image intensitites.
There are different ways of handling the two-parameter scale variations in this family of image descriptors. If we keep the local scale parameter
fixed and apply increasingly broadened versions of the window function by increasing the integration scale parameter 
only, then we obtain a true formal scale-space representation of the directional data computed at the given local scale 
. If we couple the local scale and integration scale by a relative integration scale 
, such that 
then for any fixed value of 
, we obtain a reduced self-similar one-parameter variation, which is frequently used to simplify computational algorithms, for example in corner detection
, interest point detection
, texture analysis and image matching
.
By varying the relative integration scale
in such a self-similar scale variation, we obtain another alternative way of parameterizing the multi-scale nature of directional data obtained by increasing the integration scale.
A conceptually similar construction can be performed for discrete signals, with the convolution integral replaced by a convolution sum and with the continuous Gaussian kernel
replaced by the discrete Gaussian kernel 
:
When quantizing the scale parameters
and 
in an actual implementation, a finite geometric progression 
is usually used, with i ranging from 0 to some maximum scale index m. Thus, the discrete scale levels will bear certain similarities to image pyramid
, although spatial subsampling may not necessarily be used in order to preserve more accurate data for subsequent processing stages.
, interest point detection
, and feature tracking. The structure tensor also plays a central role in the Lucas-Kanade optical flow algorithm, and in its extensions to estimate affine shape adaptation
; where the magnitude of
is an indicator of the reliability of the computed result. The tensor has also been used for scale-space analysis, estimation of local surface orientation from monocular or binocular cues, non-linear fingerprint enhancement, diffusion-based image processing, and several other image processing problems.
If one in this context aims at image descriptors that are invariant under Galilean transformations, to make it possible to compare image measurements that have been obtained under variations of a priori unknown image velocities
,
it is, however, from a computational viewpoint more preferable to parameterize the components in the structure tensor/second-moment matrix
using the notion of Galilean diagonalization
where
denotes a Galilean transformation of space-time and 
a two-dimensional rotation over the spatial domain,
compared to the abovementioned use of eigenvalues of a 3-D structure tensor, which corresponds to an eigenvalue decomposition and a (non-physical) three-dimensional rotation of space-time
.
To obtain true Galilean invariance, however, also the shape of the spatio-temporal window function needs to be adapted, corresponding to the transfer of affine shape adaptation
from spatial to spatio-temporal image data.
In combination with local spatio-temporal histogram descriptors,
these concepts together allow for Galilean invariant recognition of spatio-temporal events.
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, also referred to as the second-moment matrix, is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
derived from the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. It summarizes the predominant directions of the gradient in a specified neighborhood of a point, and the degree to which those directions are coherent. The structure tensor is often used in image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
.
Continuous version
For a function of two variables p=(x,y), the structure tensor is the 2×2 matrixwhere
and are the partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of
with respect to x and y; the integrals range over the plane ; and w is some fixed "window function", a distributionDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
on two variables. Note that the matrix Sw is itself a function of p=(x,y).
The formula above can be written also as
, where is the matrix-valued function defined byIf the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of is viewed as a 1×2 (single-row) matrix, the matrix can be written as the matrix product , where denotes the 2×1 (single-column) transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of the gradient. (Note however that the structure tensor
cannot be factored in this way.)Discrete version
In image processing and other similar applications, the function is usually given as a discrete array of samples , where p is a pair of integer indices. The 2D structure tensor at a given pixelPixel
In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
is usually taken to be the discrete sum
Here the summation index r ranges over a finite set of index pairs (the "window", typically
for some m), and w[r] is a fixed "window weight" that depends on r, such that the sum of all weights is 1. The values are the partial derivatives sampled at pixel p; which, for instance, may be estimated from by by finite differenceFinite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
formulas.
The formula of the structure tensor can be written also as
, where is the matrix-valued array such thatInterpretation
The importance of the 2D structure tensor stems from the fact that its eigenvalues (which can be ordered so that ) and the corresponding eigenvectors summarize the distribution of the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of within the window defined by centered at .Namely, if
, then (or ) is the direction that is maximally aligned with the gradient within the window. In particular, if then the gradient is always a multiple of (positive, negative or zero); this is the case if and only if within the window varies along the direction but is constant along .If
, on the other hand, the gradient in the window has no predominant direction; which happens, for instance, when the image has rotational symmetryRotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
within that window. In particular,
if and only if the function is constant () within .More generally, the value of
, for k=1 or k=2, is the -weighted average, in the neighborhood of p, of the square of the directional derivativeDirectional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of
along . The relative discrepancy between the two eigenvalues of is an indicator of the degree of anisotropyIsotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
of the gradient in the window, namely how strongly is its biased towards a particular direction (and its opposite). This attribute can be quantified by the coherence, defined as
if
. This quantity is 1 when the gradient is totally aligned, and 0 when it has no preferred direction. The formula is undefined, even in the limitLimit
A limit can be:* Limit :** Limit of a function** Limit of a sequence** One-sided limit** Limit superior and limit inferior** Limit of a net** Limit point** Limit ** Direct limit and Inverse limit...
, when the image is constant in the window (
). Some authors define it as 0 in that case.Note that the average of the gradient
inside the window is not a good indicator of anisotropy. Aligned but oppositely oriented gradient vectors would cancel out in this average, whereas in the structure tensor they are properly added together.By expanding the effective radius of the window function
(that is, increasing its variance), one can make the structure tensor more robust in the face of noise, at the cost of diminished spatial resolution. The formal basis for this property is described in more detail below, where it is shown that a multi-scale formulation of the structure tensor, referred to as the multi-scale structure tensor, constitutes a true multi-scale representation of directional data under variations of the spatial extent of the window function.Definition
The structure tensor can be defined also for a function of three variables p=(x,y,z) in an entirely analogous way. Namely, in the continuous version we have , wherewhere
are the three partial derivatives of , and the integral ranges over . In the discrete version,, whereand the sum ranges over a finite set of 3D indices, usually
for some m.Interpretation
As in the two-dimensional case, the eigenvalues of , and the corresponding eigenvectors , summarize the distribution of gradient directions within the neighborhood of p defined by the window . This information can be visualized as an ellipsoid whose semi-axes are equal to the eigenvalues and directed along their corresponding eigenvectors. is much larger than both and ), it means that the gradient in the window is predominantly aligned with the direction , so that the isosurfaceIsosurface
An isosurface is a three-dimensional analog of an isoline. It is a surface that represents points of a constant value within a volume of space; in other words, it is a level set of a continuous function whose domain is 3D-space.Isosurfaces are normally displayed using computer graphics, and are...
s of
tend to be flat and perpendicular to that vector. This situation occurs, for instance, when p lies on a thin plate-like feature, or on the smooth boundary between two regions with contrasting values. |  |  |
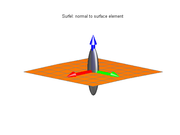If the ellipsoid is flattened in one direction only, like a pancake (that is, if
is much smaller than both and ), it means that the gradient directions are spread out but perpendicular to ; so that the isosurfaces tend to be like tubes parallel to that vector. This situation occurs, for instance, when p lies on a thin line-like feature, or on a sharp corner of the boundary between two regions with contrasting values. |  |  |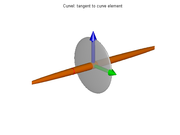
Finally, if the ellipsoid is roughly spherical (that is, if
), it means that the gradient directions in the window are more or less evenly distributed, with no marked preference; so that the function is mostly isotropic in that neighborhood. This happens, for instance, when the function has spherical symmetry in the neighborhood of p. In particular, if the ellipsoid degenerates to a point (that is, if the three eigenvalues are zero), it means that is constant (has zero gradient) within the window. |  |  |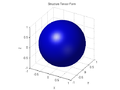
The multi-scale structure tensor
The structure tensor is an important tool in scale-space analysis. The multi-scale structure tensor (or multi-scale second moment matrix) of a function is in contrast to other one-parameter scale-space features an image descriptor that is defined over two scale parameters.One scale parameter, referred to as local scale
, is needed for determining the amount of pre-smoothing when computing the image gradient . Another scale parameter, referred to as integration scale , is needed for specifying the spatial extent of the window function that determines the weights for the region in space over which the components of the outer product of the gradient by itself are accumulated.More precisely, suppose that
is a real-valued signal defined over . For any local scale , let a multi-scale representation of this signal be given by where represents a pre-smoothing kernel. Furthermore, let denote the gradient of the scale-space representation.Then, the multi-scale structure tensor/second-moment matrix is defined by
Conceptually, one may ask if it would be sufficient to use any self-similar families of smoothing functions
and . If one naively would apply, for example, a box filter, however, then non-desirable artifacts could easily occur. If one wants the multi-scale structure tensor to be well-behaved over both increasing local scales and increasing integration scales , then it can be shown that both the smoothing function and the window function have to be Gaussian. The conditions that specifify this uniqueness are similar to the scale-space axiomsScale-space axioms
In image processing and computer vision, a scale-space framework can be used to represent an image as a family of gradually smoothed images. This framework is very general and a variety of scale-space representations exist...
that are used for deriving the uniqueness of the Gaussian kernel for a regular Gaussian scale-space of image intensitites.
There are different ways of handling the two-parameter scale variations in this family of image descriptors. If we keep the local scale parameter
fixed and apply increasingly broadened versions of the window function by increasing the integration scale parameter only, then we obtain a true formal scale-space representation of the directional data computed at the given local scale . If we couple the local scale and integration scale by a relative integration scale , such that then for any fixed value of , we obtain a reduced self-similar one-parameter variation, which is frequently used to simplify computational algorithms, for example in corner detectionCorner detection
Corner detection is an approach used within computer vision systems to extract certain kinds of features and infer the contents of an image. Corner detection is frequently used in motion detection, image registration, video tracking, image mosaicing, panorama stitching, 3D modelling and object...
, interest point detection
Interest point detection
Interest point detection is a recent terminology in computer vision that refers to the detection of interest points for subsequent processing...
, texture analysis and image matching
Image registration
Image registration is the process of transforming different sets of data into one coordinate system. Data may be multiple photographs, data from different sensors, from different times, or from different viewpoints. It is used in computer vision, medical imaging, military automatic target...
.
By varying the relative integration scale
in such a self-similar scale variation, we obtain another alternative way of parameterizing the multi-scale nature of directional data obtained by increasing the integration scale.A conceptually similar construction can be performed for discrete signals, with the convolution integral replaced by a convolution sum and with the continuous Gaussian kernel
replaced by the discrete Gaussian kernel :When quantizing the scale parameters
and in an actual implementation, a finite geometric progression is usually used, with i ranging from 0 to some maximum scale index m. Thus, the discrete scale levels will bear certain similarities to image pyramidPyramid (image processing)
Pyramid or pyramid representation is a type of multi-scale signal representation developed by the computer vision, image processing and signal processing communities, in which a signal or an image is subject to repeated smoothing and subsampling...
, although spatial subsampling may not necessarily be used in order to preserve more accurate data for subsequent processing stages.
Applications
The eigenvalues of the structure tensor play a significant role in many image processing algorithms, for problems like corner detectionCorner detection
Corner detection is an approach used within computer vision systems to extract certain kinds of features and infer the contents of an image. Corner detection is frequently used in motion detection, image registration, video tracking, image mosaicing, panorama stitching, 3D modelling and object...
, interest point detection
Interest point detection
Interest point detection is a recent terminology in computer vision that refers to the detection of interest points for subsequent processing...
, and feature tracking. The structure tensor also plays a central role in the Lucas-Kanade optical flow algorithm, and in its extensions to estimate affine shape adaptation
Affine shape adaptation
Affine shape adaptation is a methodology for iteratively adapting the shape of the smoothing kernels in an affine group of smoothing kernels to the local image structure in neighbourhood region of a specific image point...
; where the magnitude of
is an indicator of the reliability of the computed result. The tensor has also been used for scale-space analysis, estimation of local surface orientation from monocular or binocular cues, non-linear fingerprint enhancement, diffusion-based image processing, and several other image processing problems.Processing spatio-temporal video data with the structure tensor
The three-dimensional structure tensor has been used to analyze three-dimensional video data (viewed as a function of x, y, and time t).If one in this context aims at image descriptors that are invariant under Galilean transformations, to make it possible to compare image measurements that have been obtained under variations of a priori unknown image velocities
,it is, however, from a computational viewpoint more preferable to parameterize the components in the structure tensor/second-moment matrix
using the notion of Galilean diagonalizationwhere
denotes a Galilean transformation of space-time and a two-dimensional rotation over the spatial domain,compared to the abovementioned use of eigenvalues of a 3-D structure tensor, which corresponds to an eigenvalue decomposition and a (non-physical) three-dimensional rotation of space-time
.To obtain true Galilean invariance, however, also the shape of the spatio-temporal window function needs to be adapted, corresponding to the transfer of affine shape adaptation
Affine shape adaptation
Affine shape adaptation is a methodology for iteratively adapting the shape of the smoothing kernels in an affine group of smoothing kernels to the local image structure in neighbourhood region of a specific image point...
from spatial to spatio-temporal image data.
In combination with local spatio-temporal histogram descriptors,
these concepts together allow for Galilean invariant recognition of spatio-temporal events.
See also
- TensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
- Directional derivativeDirectional derivativeIn mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
- GaussianGAUSSIANGaussian is a computational chemistry software program initially released in 1970 by John Pople and his research group at Carnegie-Mellon University as Gaussian 70. It has been continuously updated since then...
- Corner detectionCorner detectionCorner detection is an approach used within computer vision systems to extract certain kinds of features and infer the contents of an image. Corner detection is frequently used in motion detection, image registration, video tracking, image mosaicing, panorama stitching, 3D modelling and object...
- Edge detectionEdge detectionEdge detection is a fundamental tool in image processing and computer vision, particularly in the areas of feature detection and feature extraction, which aim at identifying points in a digital image at which the image brightness changes sharply or, more formally, has discontinuities...
- Lucas-Kanade methodLucas Kanade methodIn computer vision, the Lucas–Kanade method is a widely used differential method for optical flow estimation developed by Bruce D. Lucas and Takeo Kanade...
- Affine shape adaptationAffine shape adaptationAffine shape adaptation is a methodology for iteratively adapting the shape of the smoothing kernels in an affine group of smoothing kernels to the local image structure in neighbourhood region of a specific image point...