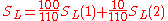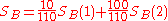Simpson's paradox
Encyclopedia
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Simpson's paradox (or the Yule–Simpson effect) is a paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
in which a correlation present in different groups is reversed when the groups are combined. This result is often encountered in social-science and medical-science statistics, and it occurs when frequency
data are hastily given causal interpretations. Simpson's Paradox disappears when causal relations are brought into consideration (see Implications to decision making).
Though it is mostly unknown to laymen
Layman
A layperson or layman is a person who is not an expert in a given field of knowledge. The term originally meant a member of the laity, i.e. a non-clergymen, but over the centuries shifted in definition....
, Simpson's Paradox is well known to statisticians, and it is described in a few introductory statistics books. Many statisticians believe that the mainstream public should be informed of the counter-intuitive results in statistics such as Simpson's paradox.
Edward H. Simpson first described this phenomenon in a technical paper in 1951,
but the statisticians Karl Pearson
Karl Pearson
Karl Pearson FRS was an influential English mathematician who has been credited for establishing the disciplineof mathematical statistics....
, et al., in 1899,
and Udny Yule
Udny Yule
George Udny Yule FRS , usually known as Udny Yule, was a British statistician, born at Beech Hill, a house in Morham near Haddington, Scotland and died in Cambridge, England. His father, also George Udny Yule, and a nephew, were knighted. His uncle was the noted orientalist Sir Henry Yule...
, in 1903, had mentioned similar effects earlier.
The name Simpson's paradox was introduced by Colin R. Blyth in 1972.
Since Edward Simpson did not actually discover this statistical paradox,See Stigler's law of eponymy
Stigler's law of eponymy
Stigler's law of eponymy is a process proposed by University of Chicago statistics professor Stephen Stigler in his 1980 publication "Stigler’s law of eponymy". In its simplest and strongest form it says: "No scientific discovery is named after its original discoverer." Stigler named the...
some writers, instead, have used the impersonal names reversal paradox and amalgamation paradox in referring to what is now called Simpson's Paradox and the Yule-Simpson effect.
Civil Rights Act of 1964
A real-life example is the passage of the Civil Rights Act of 1964Civil Rights Act of 1964
The Civil Rights Act of 1964 was a landmark piece of legislation in the United States that outlawed major forms of discrimination against African Americans and women, including racial segregation...
in the United States
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
. Overall, a larger fraction of Republican legislators voted in favor of the Act than Democrats. However, when the congressional delegations from the northern and southern
Confederate States of America
The Confederate States of America was a government set up from 1861 to 1865 by 11 Southern slave states of the United States of America that had declared their secession from the U.S...
States are considered separately, a larger fraction of Democrats voted in favor of the act in both regions. This arose because regional affiliation is a very strong indicator of how a congressman or senator voted, but party affiliation is a weak indicator.
| House | Democrat | Republican |
|---|---|---|
| Northern | 94% (145/154) | 85% (138/162) |
| Southern | 7% (7/94) | 0% (0/10) |
| Both | 61% (152/248) | 80% (138/172) |
| Senate | Democrat | Republican |
|---|---|---|
| Northern | 98% (45/46) | 84% (27/32) |
| Southern | 5% (1/21) | 0% (0/1) |
| Both | 69% (46/67) | 82% (27/33) |
Kidney stone treatment
This is another real-life example from a medical study comparing the success rates of two treatments for kidney stoneKidney stone
A kidney stone, also known as a renal calculus is a solid concretion or crystal aggregation formed in the kidneys from dietary minerals in the urine...
s.
The table shows the success rates and numbers of treatments for treatments involving both small and large kidney stones, where Treatment A includes all open procedures and Treatment B is percutaneous nephrolithotomy
Percutaneous nephrolithotomy
Percutaneous nephrolithotomy is a surgical procedure to remove stones from the kidney by a small puncture wound through the skin. It is most suitable to remove stones of more than 2 cm in size. It is usually done under general anesthesia or spinal anesthesia.- Procedure :A Retrograde pyelogram is...
:
| Treatment A | Treatment B | |
|---|---|---|
| Small Stones | Group 1 93% (81/87) |
Group 2 87% (234/270) |
| Large Stones | Group 3 73% (192/263) |
Group 4 69% (55/80) |
| Both | 78% (273/350) | 83% (289/350) |
The paradoxical conclusion is that treatment A is more effective when used on small stones, and also when used on large stones, yet treatment B is more effective when considering both sizes at the same time. In this example the "lurking" variable (or confounding variable
Confounding
In statistics, a confounding variable is an extraneous variable in a statistical model that correlates with both the dependent variable and the independent variable...
) of the stone size was not previously known to be important until its effects were included.
Which treatment is considered better is determined by an inequality between two ratios (successes/total). The reversal of the inequality between the ratios, which creates Simpson's paradox, happens because two effects occur together:
- The sizes of the groups, which are combined when the lurking variable is ignored, are very different. Doctors tend to give the severe cases (large stones) the better treatment (A), and the milder cases (small stones) the inferior treatment (B). Therefore, the totals are dominated by groups three and two, and not by the two much smaller groups one and four.
- The lurking variable has a large effect on the ratios, i.e. the success rate is more strongly influenced by the severity of the case than by the choice of treatment. Therefore, the group of patients with large stones using treatment A (group three) does worse than the group with small stones, even if the latter used the inferior treatment B (group two).
Berkeley gender bias case
One of the best known real life examples of Simpson's paradox occurred when the University of California, BerkeleyUniversity of California, Berkeley
The University of California, Berkeley , is a teaching and research university established in 1868 and located in Berkeley, California, USA...
was sued for bias against women who had applied for admission to graduate school
Graduate school
A graduate school is a school that awards advanced academic degrees with the general requirement that students must have earned a previous undergraduate degree...
s there. The admission figures for the fall of 1973 showed that men applying were more likely than women to be admitted, and the difference was so large that it was unlikely to be due to chance.
| Applicants | Admitted | |
|---|---|---|
| Men | 8442 | 44% |
| Women | 4321 | 35% |
But when examining the individual departments, it appeared that no department was significantly biased against women. In fact, most departments had a "small but statistically significant
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
bias in favor of women." The data from the six largest departments are listed below.
| Department | Men | Women | ||
|---|---|---|---|---|
| Applicants | Admitted | Applicants | Admitted | |
| A | 825 | 62% | 108 | 82% |
| B | 560 | 63% | 25 | 68% |
| C | 325 | 37% | 593 | 34% |
| D | 417 | 33% | 375 | 35% |
| E | 191 | 28% | 393 | 24% |
| F | 272 | 6% | 341 | 7% |
The research paper by Bickel, et al. concluded that women tended to apply to competitive departments with low rates of admission even among qualified applicants (such as in the English Department), whereas men tended to apply to less-competitive departments with high rates of admission among the qualified applicants (such as in engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
). The conditions under which the admissions' frequency data from specific departments constitute a proper defense against charges of
discrimination are formulated in the book Causality by Pearl
Judea Pearl
Judea Pearl is a computer scientist and philosopher, best known for developing the probabilistic approach to artificial intelligence and the development of Bayesian networks ....
.
Low birth weight paradox
The low birth weight paradox is an apparently paradoxParadox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
ical observation relating to the birth weight
Weight
In science and engineering, the weight of an object is the force on the object due to gravity. Its magnitude , often denoted by an italic letter W, is the product of the mass m of the object and the magnitude of the local gravitational acceleration g; thus:...
s and mortality of children born to tobacco smoking
Tobacco smoking
Tobacco smoking is the practice where tobacco is burned and the resulting smoke is inhaled. The practice may have begun as early as 5000–3000 BCE. Tobacco was introduced to Eurasia in the late 16th century where it followed common trade routes...
mothers. As a usual practice, babies weighing less than a certain amount (which varies between different countries) have been classified as having low birth weight
Low birth weight
Low birth weight is defined as a birth weight of a liveborn infant of less than 2,500 g. regardless of gestational age-Causes:LBW is either the result of preterm birth or of the infant being small for gestational age , or a combination of...
. In a given population, babies with low birth weights have had a significantly higher infant mortality
Infant mortality
Infant mortality is defined as the number of infant deaths per 1000 live births. Traditionally, the most common cause worldwide was dehydration from diarrhea. However, the spreading information about Oral Re-hydration Solution to mothers around the world has decreased the rate of children dying...
rate than others. However, it has been observed that babies of low birth weights born to smoking mothers have a lower mortality rate than the babies of low birth weights of non-smokers.
Batting averages
A common example of Simpson's Paradox involves the batting averageBatting average
Batting average is a statistic in both cricket and baseball that measures the performance of cricket batsmen and baseball hitters. The two statistics are related in that baseball averages are directly descended from the concept of cricket averages.- Cricket :...
s of players in professional baseball
Professional baseball
Baseball is a team sport which is played by several professional leagues throughout the world. In these leagues, and associated farm teams, players are selected for their talents and are paid to play for a specific team or club system....
. It is possible for one player to hit for a higher batting average than another player during a given year, and to do so again during the next year, but to have a lower batting average when the two years are combined. This phenomenon can occur when there are large differences in the number of at-bats between the years. (The same situation applies to calculating batting averages for the first half of the baseball season, and during the second half, and then combining all of the data for the season's batting average.)
A real-life example is provided by Ken Ross and involves the batting average of two baseball players, Derek Jeter
Derek Jeter
Derek Sanderson Jeter is an American baseball shortstop who has played 17 years in Major League Baseball for the New York Yankees. A twelve-time All-Star and five-time World Series champion, Jeter's clubhouse presence, on-field leadership, hitting ability, and baserunning have made him a central...
and David Justice
David Justice
David Christopher Justice is a former outfielder and designated hitter in Major League Baseball who played for the Atlanta Braves , Cleveland Indians , New York Yankees , and Oakland Athletics .-Early life:David was born in Cincinnati, Ohio, the son of Robert and Nettie Justice...
, during the baseball years 1995 and 1996:
| 1995 | 1996 | Combined | ||||
|---|---|---|---|---|---|---|
| Derek Jeter | 12/48 | .250 | 183/582 | .314 | 195/630 | .310 |
| David Justice | 104/411 | .253 | 45/140 | .321 | 149/551 | .270 |
In both 1995 and 1996, Justice had a higher batting average (in bold type) than Jeter did. However, when the two baseball seasons are combined, Jeter shows a higher batting average than Justice. According to Ross, this phenomenon would be observed about once per year among the possible pairs of interesting baseball players. In this particular case, the Simpson's Paradox can still be observed if the year 1997 is also taken into account:
| 1995 | 1996 | 1997 | Combined | |||||
|---|---|---|---|---|---|---|---|---|
| Derek Jeter | 12/48 | .250 | 183/582 | .314 | 190/654 | .291 | 385/1284 | .300 |
| David Justice | 104/411 | .253 | 45/140 | .321 | 163/495 | .329 | 312/1046 | .298 |
The Jeter and Justice example of Simpson's paradox was referred to in the "Conspiracy Theory" episode of the television series Numb3rs
NUMB3RS
Numb3rs is an American television drama which premiered on CBS on January 23, 2005, and concluded on March 12, 2010. The series was created by Nicolas Falacci and Cheryl Heuton, and follows FBI Special Agent Don Eppes and his mathematical genius brother, Charlie Eppes , who helps Don solve crimes...
, though a chart shown omitted some of the data, and listed the 1996 averages as 1995.
Description
Wikipedia
Wikipedia is a free, web-based, collaborative, multilingual encyclopedia project supported by the non-profit Wikimedia Foundation. Its 20 million articles have been written collaboratively by volunteers around the world. Almost all of its articles can be edited by anyone with access to the site,...
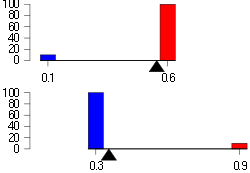
articles for two weeks. In the first week, Lisa improves 60% of the 100 articles she edited, and Bart improves 90% of 10 articles he edited. In the second week, Lisa improves just 10% of 10 articles she edited, while Bart improves 30% of 100 articles he edited.
| Week 1 | Week 2 | Total | |
|---|---|---|---|
| Lisa | 60/100 | 1/10 | 61/110 |
| Bart | 9/10 | 30/100 | 39/110 |
Both times Bart improved a higher percentage of articles than Lisa, but the actual number of articles each edited (the bottom number of their ratios also known as the sample size
Sample size
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
) were not the same for both of them either week. When the totals for the two weeks are added together, Bart and Lisa's work can be judged from an equal sample size, i.e. the same number of articles edited by each. Looked at in this more accurate manner, Lisa's ratio is higher and, therefore, so is her percentage. Also when the two tests are combined using a weighted average, overall, Lisa has improved a much higher percentage than Bart because the quality modifier had a significantly higher percentage. Therefore, like other paradoxes, it only appears to be a paradox because of incorrect assumptions, incomplete or misguided information, or a lack of understanding a particular concept.
| Week 1 quantity | Week 2 quantity | Total quantity and weighted quality | |
|---|---|---|---|
| Lisa | 60% | 10% | 55.5% |
| Bart | 90% | 30% | 35.5% |
This imagined paradox is caused when the percentage is provided but not the ratio. In this example, if only the 90% in the first week for Bart was provided but not the ratio (9:10), it would distort the information causing the imagined paradox. Even though Bart's percentage is higher for the first and second week, when two weeks of articles is combined, overall Lisa had improved a greater proportion, 55% of the 110 total articles. Lisa's proportional total of articles improved exceeds Bart's total.
Here are some notations:
- In the first week
-
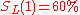— Lisa improved 60% of the many articles she edited. -
— Bart had a 90% success rate during that time.
- Success is associated with Bart.
- In the second week
-
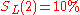— Lisa managed 10% in her busy life. -
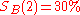— Bart achieved a 30% success rate.
- Success is associated with Bart.
On both occasions Bart's edits were more successful than Lisa's. But if we combine the two sets, we see that Lisa and Bart both edited 110 articles, and:
-
— Lisa improved 61 articles. -
— Bart improved only 39. -
— Success is now associated with Lisa.
Bart is better for each set but worse overall.
The paradox stems from the intuition that Bart could not possibly be a better editor on each set but worse overall. Pearl proved how this is possible, when "better editor" is taken in the counterfactual sense: "Were Bart to edit all items in a set he would do better than Lisa would, on those same items". Clearly, frequency data cannot support this sense of "better editor," because it does not tell us how Bart would perform on items edited by Lisa, and vice versa. In the back of our mind, though, we assume that the articles were assigned at random to Bart and Lisa, an assumption which (for large sample) would support the counterfactual interpretation of "better editor." However, under random assignment conditions, the data given in this example is impossible, which accounts for our surprise when confronting the rate reversal.
The arithmetical basis of the paradox is uncontroversial. If
and 
we feel that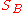 
must be greater than 
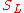. However if different weights are used to form the overall score for each person then this feeling may be disappointed. Here the first test is weighted 
for Lisa and 
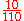for Bart while the weights are reversed on the second test.
By more extreme reweighting Lisa's overall score can be pushed up towards 60% and Bart's down towards 30%.
Lisa is a better editor on average, as her overall success rate is higher. But it is possible to have told the story in a way which would make it appear obvious that Bart is more diligent.
Simpson's paradox shows us an extreme example of the importance of including data about possible confounding variables when attempting to calculate causal relations. Precise criteria for selecting a set of "confounding variables,"
(i.e., variables that yield correct causal relationships if included in the analysis),
is given in Pearl using causal graphs.
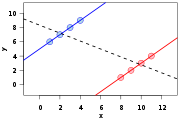
While Simpson's paradox often refers to the analysis of count tables, as shown in this example, it also occurs with continuous data: for example, if one fits separated regression line
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
s through two sets of data, the two regression lines may show a positive trend, while a regression line fitted through all data together will show a negative trend, as shown on the picture above.
Vector interpretation
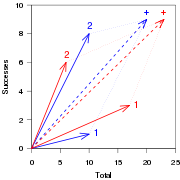
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. A success rate of
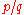can be represented by a vector 
, with a slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of
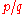. If two rates 
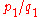and 
are combined, as in the examples given above, the result can be represented by the sum of the vectors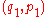 
and 
, which according to the parallelogram rule is the vector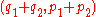 
, with slope 
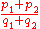.Simpson's paradox says that even if a vector
(in blue in the figure) has a smaller slope than another vector 
(in red), and 
has a smaller slope than 
, the sum of the two vectors 
(indicated by "+" in the figure) can still have a larger slope than the sum of the two vectors 
, as shown in the example.Implications to decision making
The practical significance of Simpson's paradox surfaces in decision making situations where it poses the following dilemma: Which data should we consult in choosing an action, the aggregated or the partitioned? In the Kidney Stone example above, it is clear that if one is diagnosed with "Small Stones" or "Large Stones" the data for the respective subpopulation should be consulted and Treatment A would be preferred to Treatment B. But what if a patient is not diagnosed, and the size of the stone is not known; would it be appropriate to consult the aggregated data and administer Treatment B? This would stand contrary to common sense; a treatment that is preferred both under one condition and under its negation should also be preferred when the condition is unknown.On the other hand, if the partitioned data is to be preferred a priori, what prevents one from partitioning the data into arbitrary sub-categories (say based on eye color or post-treatment pain) artificially constructed to yield wrong choices of treatments? Pearl shows that, indeed, in many cases it is the aggregated, not the partitioned data that gives the correct choice of action. Worse yet, given the same table, one should sometimes follow the partitioned and sometimes the aggregated data, depending on the story behind the data; with each story dictating its own choice. Pearl considers this to be the real paradox behind Simpson's reversal.
As to why and how a story, not data, should dictate choices, the answer is that it is the story which encodes the causal relationships among the variables. Once we extract these relationships and represent them in a graph called a causal Bayesian network we can test algorithmically whether a given partition, representing confounding variables, gives the correct answer. The test, called "back-door," requires that we check whether the nodes corresponding to the confounding variables intercept certain paths in the graph. This reduces Simpson's Paradox to an exercise in graph theory.
How likely is Simpson’s paradox?
If a 2 × 2 × 2 table, such as in thekidney stone example,
is selected at random, the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
is approximately 1/60 that
Simpson's paradox will occur purely by chance.
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: " Simpson's Paradox" – by Gary Malinas. - Earliest known uses of some of the words of mathematics: S
- For a brief history of the origins of the paradox see the entries "Simpson's Paradox" and "Spurious Correlation"
- Pearl, Judea, ""The Art and Science of Cause and Effect." A slide show and tutorial lecture.
- Pearl, Judea, "Simpson's Paradox: An Anatomy" (PDF)
- Short articles by Alexander Bogomolny at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
: - The Wall Street Journal column "The Numbers Guy" for December 2, 2009 dealt with recent instances of Simpson's paradox in the news. Notably a Simpson's paradox in the comparison of unemployment rates of the 2009 recession with the 1983 recession. by Cari Tuna (substituting for regular columnist Carl Bialik)