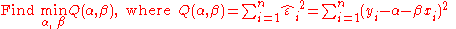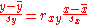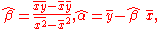Simple linear regression - AbsoluteAstronomy.com

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, simple linear regression is the least squares

Ordinary least squares

In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...

estimator of a linear regression model with a single explanatory variable

Covariate

In statistics, a covariate is a variable that is possibly predictive of the outcome under study. A covariate may be of direct interest or it may be a confounding or interacting variable....

. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...

of the model (that is, vertical distances between the points of the data set and the fitted line) as small as possible.

The adjective simple refers to the fact that this regression is one of the simplest in statistics. The fitted line has the slope equal to the correlation between y and x corrected by the ratio of standard deviations of these variables. The intercept of the fitted line is such that it passes through the center of mass (x, y) of the data points.

Other regression methods besides the simple ordinary least squares

Ordinary least squares

(OLS) also exist (see linear regression model). In particular, when one wants to do regression by eye, people usually tend to draw a slightly steeper line, closer to the one produced by the total least squares

Deming regression

In statistics, Deming regression, named after W. Edwards Deming, is an errors-in-variables model which tries to find the line of best fit for a two-dimensional dataset...

method. This occurs because it is more natural for one's mind to consider the orthogonal distances from the observations to the regression line, rather than the vertical ones as OLS method does.

Fitting the regression line

Suppose there are n data points {y_i, x_i}, where i = 1, 2, …, n. The goal is to find the equation of the straight line

which would provide a "best" fit for the data points. Here the "best" will be understood as in the least-squares

Ordinary least squares

approach: such a line that minimizes the sum of squared residuals of the linear regression model. In other words, numbers α and β solve the following minimization problem:

By using either calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

, the geometry of inner product space

Inner product space

In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...

s or simply expanding to get a quadratic in α and β, it can be shown that the values of α and β that minimize the objective function Q are

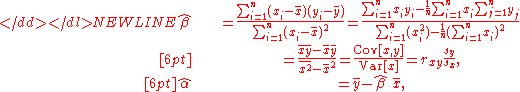
where r_xy is the sample correlation coefficient between x and y, s_x is the standard deviation

Standard deviation

Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...

of x, and s_y is correspondingly the standard deviation of y. Horizontal bar over a variable means the sample average of that variable. For example:

\overline{xy} = \tfrac{1}{n}\textstyle\sum_{i=1}^n x_iy_i\ .

Substituting the above expressions for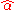

and

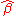into

yields

This shows the role

plays in the regression line of standardized data points.

Properties

The line goes through the "center of mass" point (x, y).
The sum of the residuals is equal to zero, if the model includes a constant:
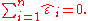
The linear combination of the residuals, in which the coefficients are the x-values, is equal to zero:
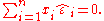
The estimators 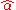and 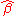are unbiased. This requires that we interpret the estimators as random variables and so we have to assume that, for each value of x, the corresponding value of y is generated as a mean response α + βx plus an additional random variable ε called the error term. This error term has to be equal to zero on average, for each value of x. Under such interpretation, the least-squares estimators 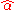and 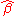will themselves be random variables, and they will unbiasedly estimate the "true values" α and β.

Linear regression without the intercept term

Sometimes, people consider a simple linear regression model without the intercept term: y = βx. In such a case, the OLS estimator for β simplifies to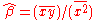

Linear regression with non-uniform errors

If the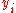

have independent, non-uniform variances

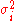, then the function Q above becomes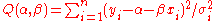

However, the OLS estimators for α and β are still given by the same equations as above,

except with the averages computed as weighted means

Weighted mean

The weighted mean is similar to an arithmetic mean , where instead of each of the data points contributing equally to the final average, some data points contribute more than others...

of the appropriate variable combinations.

Total least squares method

The above equations assume that {x_i} data are known exactly whereas {y_i} data have random distribution. In case that both {x_i} and {y_i} are random we can minimize the orthogonal distances from the observations to the regression line (total least squares method). Here we will show equation for simple linear regression model without the intercept term y = βx under the assumption that x and y have equal variances. For general case please see Deming regression

Deming regression

In statistics, Deming regression, named after W. Edwards Deming, is an errors-in-variables model which tries to find the line of best fit for a two-dimensional dataset...

.

The orthogonal distance from the observation point {y_i, x_i} to the regression line y = βx is:

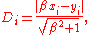where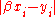

denotes absolute value

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

.

We will minimize sum of squared distances:

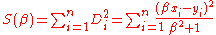
This can be solved by searching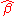

for which derivation

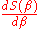is zero.

This yields the equation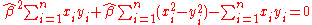

Which has the solution:

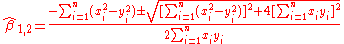
Please note that there are two different solutions (note

in the equation above). One solution represent minimum of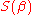

function and the other one maximum of

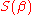function. The corresponding lines are orthogonal to each other. For

and

for all i use + sign to get the slope of the regression line.

It can be shown that if you swap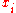

and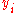

you will get slope

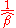. This is not the case for simple linear regression without the intercept term which is using ordinary least squares

Ordinary least squares

method.

Confidence intervals

The formulas given in the previous section allow one to calculate the point estimates of α and β — that is, the coefficients of the regression line for the given set of data. However, those formulas do not tell us how precise the estimates are. That is, how much the estimators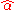

and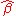

can deviate from the "true" values of α and β. The latter question is answered by the confidence intervals for the regression coefficients.

In order to construct the confidence intervals usually one of the two possible assumptions is made: either that the errors in the regression are normally distributed (the so-called classic regression assumption), or that the number of observations n is sufficiently large so that the actual distribution of the estimators can be approximated using the Central Limit Theorem

Central limit theorem

In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...

Normality assumption

Under the first assumption above, that of the normality of the error terms, the estimator of the slope coefficient will itself be normally distributed with mean β and variance

\sigma^2/\sum(x_i-\bar{x})^2,

where

is the variance of the error terms. At the same time the sum of squared residuals Q is distributed proportionally to χ² with (n−2) degrees of freedom, and independently from

\hat\beta.

This allows us to construct a t-statistic

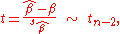where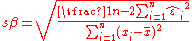

which has a Student's t-distribution with (n−2) degrees of freedom. Here s_β is the standard deviation of the estimator

\hat\beta.

Using this t-statistic we can construct a confidence interval for β:

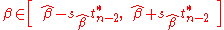at confidence level (1−γ),

where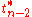

is the (1−γ/2)-th quantile of the t_n–2 distribution. For example, if γ = 0.05 then the confidence level is 95%.

Similarly, the confidence interval for the intercept coefficient α is given by

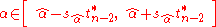at confidence level (1−γ),

where

The confidence intervals for α and β give us the general idea where these regression coefficients are most likely to be. For example in the "Okun's law" regression shown at the beginning of the article the point estimates are

\hat\alpha=0.859

and

\hat\beta=-1.817.

The 95% confidence intervals for these estimates are

with 95% confidence.

In order to represent this information graphically, in the form of the confidence bands around the regression line, one has to proceed carefully and account for the joint distribution of the estimators. It can be shown that at confidence level (1−γ) the confidence band has hyperbolic form given by the equation

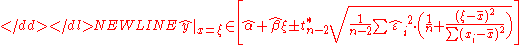
Asymptotic assumption

The alternative second assumption states that when the number of points in the dataset is "large enough", the Law of large numbers

Law of large numbers

In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...

and the Central limit theorem

Central limit theorem

become applicable, and then the distribution of the estimators is approximately normal. Under this assumption all formulas derived in the previous section remain valid, with the only exception that the quantile t*_n−2 of student-t distribution is replaced with the quantile q* of the standard normal distribution. Occasionally the fraction is replaced with . When n is large such change does not alter the results considerably.

Numerical example

As an example we shall consider the data set from the Ordinary least squares

Ordinary least squares

article. This data set gives average weights for humans as a function of their height in the population of American women of age 30–39. Although the OLS

Ordinary least squares

article argues that it would be more appropriate to run a quadratic regression for this data, we will not do so and fit the simple linear regression instead.

x_i	1.47	1.50	1.52	1.55	1.57	1.60	1.63	1.65	1.68	1.70	1.73	1.75	1.78	1.80	1.83	Height (m)
y_i	52.21	53.12	54.48	55.84	57.20	58.57	59.93	61.29	63.11	64.47	66.28	68.10	69.92	72.19	74.46	Mass (kg)

There are n = 15 points in this data set, and we start by calculating the following five sums:

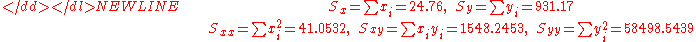
These quantities can be used to calculate the estimates of the regression coefficients, and their standard errors.

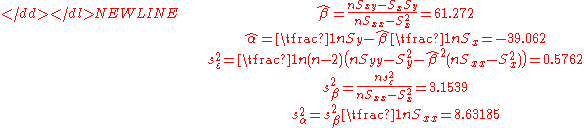
The 0.975 quantile of Student's t-distribution with 13 degrees of freedom is t^*₁₃ = 2.1604, and thus confidence intervals for α and β are

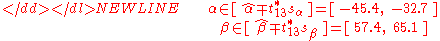
Beware

This example also demonstrates that sophisticated calculations will not overcome the use of badly prepared data. The heights were originally given in inches, and have been converted to the nearest centimetre. Since the conversion factor is one inch to 2.54cm, this is not a correct conversion. The original inches can be recovered by Round(x/0.0254) and then re-converted to metric: if this is done, the results become

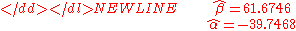
Thus a seemingly small variation in the data has a real effect.

Fitting the regression line

Properties

Linear regression without the intercept term

Linear regression with non-uniform errors

Total least squares method

Confidence intervals

Normality assumption

Asymptotic assumption

Numerical example

Beware

See also