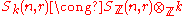Schur algebra
Encyclopedia
In mathematics, Schur algebras, named after Issai Schur
, are certain finite-dimensional algebras
closely associated with Schur–Weyl duality between general linear
and symmetric
groups. They are used to relate the representation theories
of those two groups
. Their use was promoted by the influential monograph of J. A. Green first published in 1980. The name "Schur algebra" is due to Green. In the modular case (over infinite fields
of positive characteristic) Schur algebras were used by Gordon James and Karin Erdmann to show that the (still open) problems of computing decomposition numbers for general linear groups and symmetric groups are actually equivalent. Schur algebras were used by Friedlander and Suslin
to prove finite generation of cohomology
of finite group scheme
s.
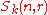makes sense for any commutative ring
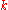. Consider the algebra
of polynomials (with coefficients in 
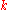) in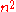 
commuting variables 
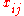, 1 ≤ i, j ≤ 
. Denote by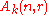 
the homogeneous polynomials of degree 
. Elements of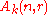 
are k-linear combinations of monomials formed by multiplying together 
of the generators 
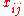(allowing repetition). Thus
Now,
has a natural coalgebra
structure with comultiplication
and counit 
the algebra homomorphisms given on generators by
Since comultiplication is an algebra homomorphism,
is a bialgebra
. One easily
checks that
is a subcoalgebra of the bialgebra 
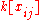, for every r ≥ 0.
Definition. The Schur algebra (in degree
) is the algebra 
. That is,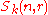 
is the linear dual of 
.
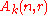It is a general fact that the linear dual
of a coalgebra
is an algebra in a natural way, where the multiplication in the algebra is induced by dualizing the comultiplication in the coalgebra. To see this, let
and, given linear functionals
, 
on 
, define their product to be the linear functional given by
The identity element for this multiplication of functionals is the counit in
.
Then the symmetric group
on 
letters acts naturally on the tensor space by place permutation, and one has an isomorphism
In other words,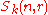
may be viewed as the algebra of endomorphisms of tensor space commuting with the action of the symmetric group
.
for any commutative ring
.
The study of these various classes of generalizations forms an active area of contemporary research.
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
, are certain finite-dimensional algebras
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
closely associated with Schur–Weyl duality between general linear
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
and symmetric
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
groups. They are used to relate the representation theories
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of those two groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. Their use was promoted by the influential monograph of J. A. Green first published in 1980. The name "Schur algebra" is due to Green. In the modular case (over infinite fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of positive characteristic) Schur algebras were used by Gordon James and Karin Erdmann to show that the (still open) problems of computing decomposition numbers for general linear groups and symmetric groups are actually equivalent. Schur algebras were used by Friedlander and Suslin
Andrei Suslin
Andrei Suslin is a Russian mathematician who has made major contributions to the field of algebra, especially algebraic K-theory and its connections with algebraic geometry. He is currently a Trustee Chair and Professor of mathematics at Northwestern University.He was born on December 27, 1950,...
to prove finite generation of cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of finite group scheme
Group scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
s.
Construction
The definition of a Schur algebra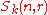 makes sense for any commutative ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
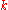. Consider the algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
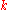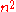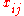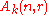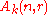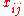of polynomials (with coefficients in ) in commuting variables , 1 ≤ i, j ≤ . Denote by the homogeneous polynomials of degree . Elements of are k-linear combinations of monomials formed by multiplying together of the generators (allowing repetition). Thus
Now,
has a natural coalgebraCoalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
structure with comultiplication
and counit the algebra homomorphisms given on generators by
(Since comultiplication is an algebra homomorphism,
is a bialgebraBialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
. One easily
checks that
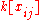is a subcoalgebra of the bialgebra , for every r ≥ 0.Definition. The Schur algebra (in degree
) is the algebra . That is, 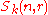is the linear dual of 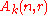.It is a general fact that the linear dual
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of a coalgebra
is an algebra in a natural way, where the multiplication in the algebra is induced by dualizing the comultiplication in the coalgebra. To see this, let
and, given linear functionals
, on , define their product to be the linear functional given by
-
.
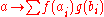The identity element for this multiplication of functionals is the counit in
.Main properties
- One of the most basic properties expresses
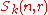as a centralizer algebra. Let 
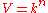be the space of rank 
column vectors over 
, and form the tensorTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
power
Then the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on letters acts naturally on the tensor space by place permutation, and one has an isomorphism
In other words,
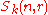may be viewed as the algebra of endomorphisms of tensor space commuting with the action of the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
.
-
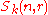is free over 
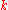of rank given by the binomial coefficient 
.
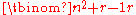- Various bases of
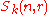are known, many of which are indexed by pairs of semistandard Young tableauYoung tableauIn mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
x of shape
, as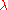 
varies over the set of partitionsPartition (number theory)In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of
into no more than 
parts.
- In case k is an infinite field,
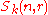may also be identified with the enveloping algebra (in the sense of H. Weyl) for the action of the general linear groupGeneral linear groupIn mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
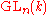acting on tensor space (via the diagonal action on tensors, induced from the natural action of 
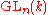on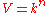 
given by matrix multiplication).
- Schur algebras are "defined over the integers". This means that they satisfy the following change of scalars property:
for any commutative ring
.- Schur algebras provide natural examples of quasihereditary algebras (as defined by Cline, Parshall, and Scott), and thus have nice homological properties. In particular, Schur algebras have finite global dimension.
Generalizations
- Generalized Schur algebras (associated to any reductive algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
) were introduced by Donkin in the 1980s. These are also quasihereditary.
- Around the same time, Dipper and James introduced the quantized Schur algebras (or q-Schur algebras for short), which are a type of q-deformation of the classical Schur algebras described above, in which the symmetric group is replaced by the corresponding Hecke algebraHecke algebraIn mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke and Nagayoshi Iwahori, is a one-parameter deformation of the group algebra of a Coxeter group....
and the general linear group by an appropriate quantum groupQuantum groupIn mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
.
- There are also generalized q-Schur algebras, which are obtained by generalizing the work of Dipper and James in the same way that Donkin generalized the classical Schur algebras.
- There are further generalizations, such as the affine q-Schur algebras related to affine Kac-Moody Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s and other generalizations, such as the cyclotomic q-Schur algebras related to Ariki-Koike algebras (which are q-deformations of certain complex reflection groupComplex reflection groupIn mathematics, a complex reflection group is a group acting on a finite-dimensional complex vector space, that is generated by complex reflections: non-trivial elements that fix a complex hyperplane in space pointwise...
s).
The study of these various classes of generalizations forms an active area of contemporary research.
See also
- There is a textbook by Stuart Martin devoted to the subject.
- Hermann Weyl'sHermann WeylHermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
classic text provides much background and motivation.
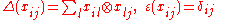