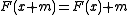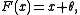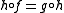Rotation number
Encyclopedia
In mathematics
, the rotation number is an invariant of homeomorphism
s of the circle
. It was first defined by Henri Poincaré
in 1885, in relation to the precession
of the perihelion of a planetary orbit
. Poincaré later proved a theorem characterizing the existence of periodic orbits in terms of rationality
of the rotation number.
of the circle
S1 = R/Z. Then f may be lifted
to a homeomorphism
F: R → R of the real line, satisfying
for every real number x and every integer m.
The rotation number of f is defined in terms of the iterates
of F:
Henri Poincaré
proved that the limit exists and is independent of the choice of the starting point x. The lift F is unique modulo integers, therefore the rotation number is a well-defined element of R/Z. Intuitively, it measures the average rotation angle along the orbits
of f.
then its rotation number is θ (cf Irrational rotation
).
for a continuous map h of the circle into itself (not necessarily homeomorphic) then f and g have the same rotation numbers. It was used by Poincaré and Arnaud Denjoy
for topological classification of homeomorphisms of the circle. There are two distinct possibilities.
Rotation number is continuous when viewed as a map from the group of homeomorphisms (with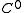
topology) of the circle into the circle.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the rotation number is an invariant of homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s of the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. It was first defined by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
in 1885, in relation to the precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
of the perihelion of a planetary orbit
Planetary orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
. Poincaré later proved a theorem characterizing the existence of periodic orbits in terms of rationality
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
of the rotation number.
Definition
Suppose that f: S1 → S1 is an orientation preserving homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
of the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
S1 = R/Z. Then f may be lifted
Lift (mathematics)
In the branch of mathematics called category theory, given a morphism f from an object X to an object Y, and a morphism g from an object Z to Y, a lift of f to Z is a morphism h from X to Z such that gh = f.A basic example in topology is lifting a path in one space to a path in a covering space...
to a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
F: R → R of the real line, satisfying
for every real number x and every integer m.
The rotation number of f is defined in terms of the iterates
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of F:
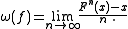
Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
proved that the limit exists and is independent of the choice of the starting point x. The lift F is unique modulo integers, therefore the rotation number is a well-defined element of R/Z. Intuitively, it measures the average rotation angle along the orbits
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
of f.
Example
If f is a rotation by θ, so that
then its rotation number is θ (cf Irrational rotation
Irrational rotation
In mathematical theory of dynamical systems, an irrational rotation is a mapwhere θ is an irrational number. Under the identification of a circle with R/Z, or with the interval [0, 1] with the boundary points glued together, this map becomes a rotation of a circle by a proportion θ of a full...
).
Properties
The rotation number is invariant under topological conjugacy, and even topological semiconjugacy: if f and g are two homeomorphisms of the circle and
for a continuous map h of the circle into itself (not necessarily homeomorphic) then f and g have the same rotation numbers. It was used by Poincaré and Arnaud Denjoy
Arnaud Denjoy
Arnaud Denjoy was a French mathematician.Denjoy was born in Auch, Gers. His contributions include work in harmonic analysis and differential equations. His integral was the first to be able to integrate all derivatives...
for topological classification of homeomorphisms of the circle. There are two distinct possibilities.
- The rotation number of f is a rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
p/q (in the lowest terms). Then f has a periodic orbit, every periodic orbit has period q, and the order of the points on each such orbit coincides with the order of the points for a rotation by p/q. Moreover, every forward orbit of f converges to a periodic orbit. The same is true for backward orbits, corresponding to iterations of f−1, but the limiting periodic orbits in forward and backward directions may be different.
- The rotation number of f is an irrational numberIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
θ. Then f has no periodic orbits (this follows immediately by considering a periodic point x of f). There are two subcases.
-
- There exists a dense orbit. In this case f is topologically conjugate to the irrational rotationIrrational rotationIn mathematical theory of dynamical systems, an irrational rotation is a mapwhere θ is an irrational number. Under the identification of a circle with R/Z, or with the interval [0, 1] with the boundary points glued together, this map becomes a rotation of a circle by a proportion θ of a full...
by the angle θ and all orbits are denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
. Denjoy proved that this possibility is always realized when f is twice continuously differentiable. - There exists a Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
C invariant under f. Then C is a unique minimal set and the orbits of all points both in forward and backward direction converge to C. In this case, f is semiconjugate to the irrational rotation by θ, and the semiconjugating map h of degree 1 is constant on components of the complement of C.
- There exists a dense orbit. In this case f is topologically conjugate to the irrational rotation
Rotation number is continuous when viewed as a map from the group of homeomorphisms (with
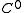topology) of the circle into the circle.See also
- Circle mapCircle mapIn mathematics, a circle map is a member of a family of dynamical systems on the circle first defined by Andrey Kolmogorov. Kolmogorov proposed this family as a simplified model for driven mechanical rotors . The circle map equations also describe a simplified model of the phase-locked loop in...
- Denjoy diffeomorphismDenjoy diffeomorphismIn mathematics, the Denjoy theorem gives a sufficient condition for a diffeomorphism of the circle to be topologically conjugate to a diffeomorphism of a special kind, namely an irrational rotation. Arnaud Denjoy proved the theorem in the course of his topological classification of homeomorphisms...
- Poincaré section
- Poincaré recurrence