Reductive dual pair
Encyclopedia
In the mathematical field of representation theory
, a reductive dual pair is a pair of subgroups (G,G ′) of the isometry group
Sp(W) of a symplectic vector space
W, such that G is the centralizer of G ′ in Sp(W) and vice versa, and these groups act reductively on W. Somewhat more loosely, one speaks of a dual pair whenever two groups are the mutual centralizers in a larger group, which is frequently a general linear group
. The concept was introduced by Roger Howe
in an influential preprint of the 1970s, which was ultimately published as .
F, which we assume to be fixed throughout. Thus W is a symplectic vector space
over F.
If W1 and W2 are two symplectic vector spaces and (G1, G1′), (G2, G2′) are two reductive dual pairs in the corresponding symplectic groups, then we may form a new symplectic vector space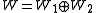
and a pair of groups 
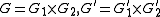acting on W by isometries. It turns out that (G,G ′) is a reductive dual pair. A reductive dual pair is called reducible if it can be obtained in this fashion from smaller groups, and irreducible otherwise. A reducible pair can be decomposed into a direct product of irreducible ones, and for many purposes, it is enough to restrict one's attention to the irreducible case.
Several classes of reductive dual pairs had appeared earlier in the work of André Weil
. Roger Howe proved a classification theorem, which states that in the irreducible case, those pairs exhaust all possibilities. An irreducible reductive dual pair (G,G ′) in Sp(W) is said to be of type II if there is a lagrangian subspace X in W that is invariant under both G and G ′, and of type I otherwise.
An archetypical irreducible reductive dual pair of type II consists of a pair of general linear group
s and arises as follows. Let U and V be two vector spaces over F,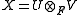
be their tensor product, and 
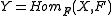its dual. Then the direct sum 
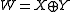can be endowed with a symplectic form such that X and Y are lagrangian subspaces, and the restriction of the symplectic form to 
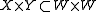coincides with the pairing between the vector space X and its dual Y. If G = GL(U) and G ′ = GL(V), then both these groups act linearly on X and Y, the actions preserve the symplectic form on W, and (G,G ′) is an irreducible reductive dual pair. Note that X is an invariant lagrangian subspace, hence this dual pair is of type II.
An archetypical irreducible reductive dual pair of type I consists of an orthogonal group
and a symplectic group and is constructed analogously. Let U be an orthogonal vector space and V be a symplectic vector space over F, and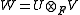
be their tensor product. The key observation is that W is a symplectic vector space whose bilinear form is obtained from the product of the forms on the tensor factors. Moreover, if G = O(U) and G ′ = Sp(V) are the isometry group
s of U and V, then they act on W in a natural way, these actions are symplectic, and (G,G ′) is an irreducible reductive dual pair of type I.
These two constructions produce all irreducible reductive dual pairs over an algebraically closed field
F, such as the field C of complex number
s. In general, one can replace vector spaces over F by vector spaces over a division algebra
D over F, and proceed similarly to above to construct an irreducible reductive dual pair of type II. For type I, one starts with a division algebra D with involution τ, a hermitian form on U, and a skew-hermitian form on V (both of them non-degenerate), and forms their tensor product over D,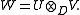
Then W is naturally endowed with a structure of a symplectic vector space over F, the isometry groups of U and V act symplectically on W and form an irreducible reductive dual pair of type I. Roger Howe proved that, up to an isomorphism, any irreducible dual pair arises in this fashion. An explicit list for the case F = R appears in .
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, a reductive dual pair is a pair of subgroups (G,G ′) of the isometry group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
Sp(W) of a symplectic vector space
Symplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
W, such that G is the centralizer of G ′ in Sp(W) and vice versa, and these groups act reductively on W. Somewhat more loosely, one speaks of a dual pair whenever two groups are the mutual centralizers in a larger group, which is frequently a general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
. The concept was introduced by Roger Howe
Roger Evans Howe
Roger Evans Howe is the William R. Kenan Jr. Professor of Mathematics at Yale University. He is well known for his contributions to representation theory, and in particular for the notion of a reductive dual pair, sometimes known as a Howe pair, and the Howe correspondence.He attended Ithaca High...
in an influential preprint of the 1970s, which was ultimately published as .
Examples
- The full symplectic group G = Sp(W) and the two-element group G ′, the centerCenter (group theory)In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of Sp(W), form a reductive dual pair. The double centralizer property is clear from the way these groups were defined: the centralizer of the group G in G is its center, and the centralizer of the center of any group is the group itself. The group G ′ consists of the identity transformation and its negative, and can be interpreted as the orthogonal group of a one-dimensional vector space. It emerges from the subsequent development of the theory that this pair is a first instance of a general family of dual pairs consisting of a symplectic group and an orthogonal group, which are known as type I irreducible reductive dual pairs.
- Let X be an n-dimensional vector space, Y be its dualDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
, and W be the direct sum of X and Y. Then W can be made into a symplectic vector space in a natural way, so that (X,Y) is its lagrangian polarization. The group G is the general linear group GL(X), which acts tautologically on X and contragrediently on Y. The centralizer of G in the symplectic group is the group G ′ consisting of linear operators on W that act on X by multiplication by a non-zero scalar λ and on Y by scalar multiplication by its inverse λ−1. Then the centralizer of G ′ is G, these two groups act completely reducibly on W, and hence form a reductive dual pair. The group G ′ can be interpreted as the general linear group of a one-dimensional vector space. This pair is a member of a family of dual pairs consisting of general linear groups known as type II irreducible reductive dual pairs.
Structure theory and classification
The notion of a reductive dual pair makes sense over any fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F, which we assume to be fixed throughout. Thus W is a symplectic vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over F.
If W1 and W2 are two symplectic vector spaces and (G1, G1′), (G2, G2′) are two reductive dual pairs in the corresponding symplectic groups, then we may form a new symplectic vector space
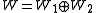and a pair of groups 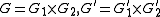acting on W by isometries. It turns out that (G,G ′) is a reductive dual pair. A reductive dual pair is called reducible if it can be obtained in this fashion from smaller groups, and irreducible otherwise. A reducible pair can be decomposed into a direct product of irreducible ones, and for many purposes, it is enough to restrict one's attention to the irreducible case.Several classes of reductive dual pairs had appeared earlier in the work of André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
. Roger Howe proved a classification theorem, which states that in the irreducible case, those pairs exhaust all possibilities. An irreducible reductive dual pair (G,G ′) in Sp(W) is said to be of type II if there is a lagrangian subspace X in W that is invariant under both G and G ′, and of type I otherwise.
An archetypical irreducible reductive dual pair of type II consists of a pair of general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
s and arises as follows. Let U and V be two vector spaces over F,
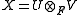be their tensor product, and 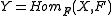its dual. Then the direct sum 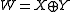can be endowed with a symplectic form such that X and Y are lagrangian subspaces, and the restriction of the symplectic form to 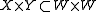coincides with the pairing between the vector space X and its dual Y. If G = GL(U) and G ′ = GL(V), then both these groups act linearly on X and Y, the actions preserve the symplectic form on W, and (G,G ′) is an irreducible reductive dual pair. Note that X is an invariant lagrangian subspace, hence this dual pair is of type II.An archetypical irreducible reductive dual pair of type I consists of an orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
and a symplectic group and is constructed analogously. Let U be an orthogonal vector space and V be a symplectic vector space over F, and
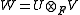be their tensor product. The key observation is that W is a symplectic vector space whose bilinear form is obtained from the product of the forms on the tensor factors. Moreover, if G = O(U) and G ′ = Sp(V) are the isometry groupIsometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
s of U and V, then they act on W in a natural way, these actions are symplectic, and (G,G ′) is an irreducible reductive dual pair of type I.
These two constructions produce all irreducible reductive dual pairs over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
F, such as the field C of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. In general, one can replace vector spaces over F by vector spaces over a division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
D over F, and proceed similarly to above to construct an irreducible reductive dual pair of type II. For type I, one starts with a division algebra D with involution τ, a hermitian form on U, and a skew-hermitian form on V (both of them non-degenerate), and forms their tensor product over D,
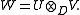Then W is naturally endowed with a structure of a symplectic vector space over F, the isometry groups of U and V act symplectically on W and form an irreducible reductive dual pair of type I. Roger Howe proved that, up to an isomorphism, any irreducible dual pair arises in this fashion. An explicit list for the case F = R appears in .See also
- Howe correspondence between representations of elements of a reductive dual pair.
- Heisenberg group
- Metaplectic groupMetaplectic groupIn mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...