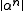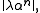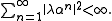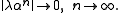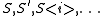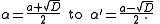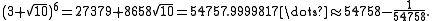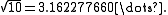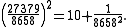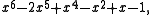Pisot-Vijayaraghavan number
Encyclopedia
In mathematics
, a Pisot–Vijayaraghavan number, also called simply a Pisot number or a PV number, is a real
algebraic integer
greater than 1 such that all its Galois conjugates are less than 1 in absolute value
. These numbers were discovered by Axel Thue
in 1912 and rediscovered by G. H. Hardy
in 1919 within the context of diophantine approximation
. They became widely known after the publication of Charles Pisot
's dissertation in 1938. The same condition also occurs in the uniqueness problem for Fourier series
. Tirukkannapuram Vijayaraghavan
and Raphael Salem
continued their study in the 1940s. Salem numbers are a closely related set of numbers.
A characteristic property of PV numbers is that their powers approach integers at an exponential rate. Pisot proved a remarkable converse: if α > 1 is a real number such that the sequence
measuring the distance from its consecutive powers to the nearest integer is square-summable
, or ℓ2, then α is a Pisot number (and, in particular, algebraic). Building on this characterization of PV numbers, Salem showed that the set S of all PV numbers is closed
. Its minimal element is a cubic irrationality known as the plastic number
. Much is known about the accumulation points of S. The smallest of them is the golden ratio
.
monic polynomial P(x) of degree n with integer coefficients, its minimal polynomial
. The other roots of P(x) are called the conjugates
of α. If α > 1 but all other roots of P(x) are real or complex
numbers of absolute value less than 1, so that they lie strictly inside the circle |x| = 1 in the complex plane
, then α is called a Pisot number, Pisot–Vijayaraghavan number, or simply PV number. For example, the golden ratio
, φ ≈ 1.618, is a real quadratic integer that is greater than 1, while the absolute value of its conjugate, −φ−1 ≈ −0.618, is less than 1. Therefore, φ is a Pisot number. Its minimal polynomial is x2 − x − 1.
where ||x|| denotes the distance from the real number x to the nearest integer, approaches 0 at an exponential rate. In particular, it is a square-summable sequence
and its terms converge to 0.
Two converse statements are known: they characterize PV numbers among all real numbers and among the algebraic numbers (but under a weaker diophantine assumption).
A longstanding Pisot–Vijayaraghavan problem asks whether the assumption that α is algebraic can be dropped from the last statement. If the answer is affirmative, Pisot's numbers would be characterized among all real numbers by the simple convergence of ||λαn|| to 0 for some auxiliary real λ. It is known that there are only countably many numbers α with this property. The problem is to decide whether any of them is transcendental.
: it contains all its limit point
s. His proof uses a constructive version of the main diophantine property of Pisot numbers: given a Pisot number α, a real number λ can be chosen so that 0 < λ ≤ α and
Thus the ℓ2 norm of the sequence ||λαn|| can be bounded by a uniform constant independent of α. In the last step of the proof, Pisot's characterization is invoked to conclude that the limit of a sequence of Pisot numbers is itself a Pisot number.
Closedness of S implies that it has a minimal element. Carl Ludwig Siegel
proved that it is the positive root of the equation x3 − x − 1 = 0 (plastic constant) and is isolated in S. He constructed two sequences of Pisot numbers converging to the golden ratio φ from below and asked whether φ is the smallest limit point of S. This was later proved by Dufresnoy and Pisot, who also determined all elements of S that less than φ; not all of them belong to Siegel's two sequences. Vijayaraghavan proved that S has infinitely many limit points; in fact, the sequence of derived sets
does not terminate. On the other hand, the intersection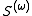
of these sets is empty, meaning that the Cantor–Bendixson rank of S is ω. Even more accurately, the order type
of S has been determined.
The set of Salem numbers, denoted by T, is intimately related with S. It has been proved that S is contained in the set T of the limit points of T. It has been conjectured that the union
of S and T is closed.
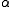is a quadratic irrational
there is only one other conjugate: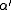
, obtained by changing the sign of the square root in 
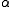from
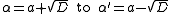
or from
Here a and D are integers and in the second case a is odd and D is congruent to 1 modulo 4.
The required conditions are α > 1 and −1 < α' < 1.
These are satisfied in the first case exactly when a > 0 and either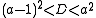
or 
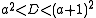. These are satisfied in the second case exactly when 
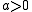and either 
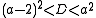or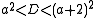 
.
The first few quadratic irrationals that are PV numbers are:
Since
and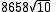 
differ by only 
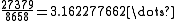is extremely close to
Indeed
Higher powers give correspondingly better rational approximations.
This property stems from the fact that for each n, the sum of nth powers of an algebraic integer x and its conjugates is exactly an integer; this follows from an application of Newton's identities
. When x is a Pisot number, the nth powers of the other conjugates tend to 0 as n tends to infinity. Since the sum is an integer, the distance from xn to the nearest integer tends to 0 at an exponential rate.
φ have been determined by Dufresnoy and Pisot. The table below lists ten smallest Pisot numbers in the increasing order. The polynomials in this table, with the exception of
are factors of either
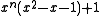
or
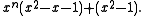
The first polynomial is divisible by x2 − 1 when n is odd and by x − 1 when n is even. It has one other real zero, which is a PV number. Dividing either polynomial by xn gives expressions that approach x2 − x − 1 as n grows very large and have zeros that converge
to φ. A complementary pair of polynomials,
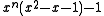
and
yields Pisot numbers that approach φ from above.
Since these PV numbers are less than 2, they are all units: their minimal polynomials end in 1 or −1.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Pisot–Vijayaraghavan number, also called simply a Pisot number or a PV number, is a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
greater than 1 such that all its Galois conjugates are less than 1 in absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
. These numbers were discovered by Axel Thue
Axel Thue
Axel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....
in 1912 and rediscovered by G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
in 1919 within the context of diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
. They became widely known after the publication of Charles Pisot
Charles Pisot
Charles Pisot was a French mathematician. He is chiefly recognized as one of the primary investigators of the numerical set associated with his name, the Pisot–Vijayaraghavan numbers....
's dissertation in 1938. The same condition also occurs in the uniqueness problem for Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. Tirukkannapuram Vijayaraghavan
Tirukkannapuram Vijayaraghavan
Tirukkannapuram Vijayaraghavan was an Indian mathematician from Madras region. He worked with G. H. Hardy when he went to Oxford in mid-1920s on Pisot-Vijayaraghavan numbers...
and Raphael Salem
Raphaël Salem
Raphaël Salem, was a Greek-Sephardic mathematician after whom are named the Salem numbers and whose widow founded the Salem Prize.-Biography:...
continued their study in the 1940s. Salem numbers are a closely related set of numbers.
A characteristic property of PV numbers is that their powers approach integers at an exponential rate. Pisot proved a remarkable converse: if α > 1 is a real number such that the sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
measuring the distance from its consecutive powers to the nearest integer is square-summable
Sequence space
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
, or ℓ2, then α is a Pisot number (and, in particular, algebraic). Building on this characterization of PV numbers, Salem showed that the set S of all PV numbers is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
. Its minimal element is a cubic irrationality known as the plastic number
Plastic number
In mathematics, the plastic number ρ is a mathematical constant which is the unique real solution of the cubic equationx^3=x+1\, ....
. Much is known about the accumulation points of S. The smallest of them is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
.
Definition and properties
An algebraic integer of degree n is a root α of an irreducibleIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
monic polynomial P(x) of degree n with integer coefficients, its minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
. The other roots of P(x) are called the conjugates
Conjugate element (field theory)
In mathematics, in particular field theory, the conjugate elements of an algebraic element α, over a field K, are the roots of the minimal polynomialof α over K.-Example:The cube roots of the number one are:...
of α. If α > 1 but all other roots of P(x) are real or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers of absolute value less than 1, so that they lie strictly inside the circle |x| = 1 in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, then α is called a Pisot number, Pisot–Vijayaraghavan number, or simply PV number. For example, the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
, φ ≈ 1.618, is a real quadratic integer that is greater than 1, while the absolute value of its conjugate, −φ−1 ≈ −0.618, is less than 1. Therefore, φ is a Pisot number. Its minimal polynomial is x2 − x − 1.
Elementary properties
- Every positive integer except 1 is a PV number. Conversely, every rational PV number is an integer greater than 1.
- If α is an irrational PV number whose minimal polynomial ends in k then α is greater than |k|. Consequently, all PV numbers that are less than 2 are algebraic units.
- If α is a PV number then so are its powers αk, for all natural exponents.
- Every real algebraic number field K of degree n contains a PV number of degree n. This number is a field generator. The set of all PV numbers of degree n in K is closed under multiplication.
- Given an upper bound M and degree n, there is only a finite number of PV numbers of degree n that are less than M.
Diophantine properties
The main interest in PV numbers is due to the fact that their powers have a very "biased" distribution (mod 1). If α is a PV number and λ is any algebraic integer in the field of α then the sequence
where ||x|| denotes the distance from the real number x to the nearest integer, approaches 0 at an exponential rate. In particular, it is a square-summable sequence
and its terms converge to 0.
Two converse statements are known: they characterize PV numbers among all real numbers and among the algebraic numbers (but under a weaker diophantine assumption).
- Let α be a real number greater than 1 and there exists a non-zero real number λ such that
- Then α is a Pisot number and λ is an algebraic number in the field of α (Pisot's theorem).
- Let α be an algebraic number greater than 1 and there exists a non-zero real number λ such that
- Then α is a Pisot number and λ is an algebraic number in the field of α.
A longstanding Pisot–Vijayaraghavan problem asks whether the assumption that α is algebraic can be dropped from the last statement. If the answer is affirmative, Pisot's numbers would be characterized among all real numbers by the simple convergence of ||λαn|| to 0 for some auxiliary real λ. It is known that there are only countably many numbers α with this property. The problem is to decide whether any of them is transcendental.
Topological properties
The set of all Pisot numbers is denoted S. Since Pisot numbers are algebraic, the set S is countable. Raphael Salem proved that this set is closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
: it contains all its limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
s. His proof uses a constructive version of the main diophantine property of Pisot numbers: given a Pisot number α, a real number λ can be chosen so that 0 < λ ≤ α and
Thus the ℓ2 norm of the sequence ||λαn|| can be bounded by a uniform constant independent of α. In the last step of the proof, Pisot's characterization is invoked to conclude that the limit of a sequence of Pisot numbers is itself a Pisot number.
Closedness of S implies that it has a minimal element. Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
proved that it is the positive root of the equation x3 − x − 1 = 0 (plastic constant) and is isolated in S. He constructed two sequences of Pisot numbers converging to the golden ratio φ from below and asked whether φ is the smallest limit point of S. This was later proved by Dufresnoy and Pisot, who also determined all elements of S that less than φ; not all of them belong to Siegel's two sequences. Vijayaraghavan proved that S has infinitely many limit points; in fact, the sequence of derived sets
Derived set (mathematics)
In mathematics, more specifically in point-set topology, the derived set of a subset S of a topological space is the set of all limit points of S...
does not terminate. On the other hand, the intersection
of these sets is empty, meaning that the Cantor–Bendixson rank of S is ω. Even more accurately, the order typeOrder type
In mathematics, especially in set theory, two ordered sets X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection f: X → Y such that both f and its inverse are monotone...
of S has been determined.
The set of Salem numbers, denoted by T, is intimately related with S. It has been proved that S is contained in the set T of the limit points of T. It has been conjectured that the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of S and T is closed.
Quadratic irrationals
If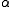 is a quadratic irrationalQuadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
there is only one other conjugate:
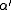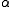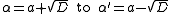
, obtained by changing the sign of the square root in fromor from
Here a and D are integers and in the second case a is odd and D is congruent to 1 modulo 4.
The required conditions are α > 1 and −1 < α
These are satisfied in the first case exactly when a > 0 and either
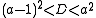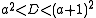or . These are satisfied in the second case exactly when 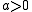and eithe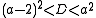r or 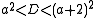.The first few quadratic irrationals that are PV numbers are:
| Value | Root of... | Numerical value |
|---|---|---|
 |
 |
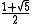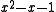1.618034... (the golden ratio Golden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... ) |
 |
 |
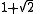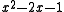2.414214... (the silver ratio Silver ratio In mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,... ) |
 |
 |
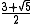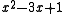2.618034... |
 |
 |
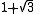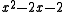2.732051... |
 |
 |
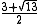3.302776... |
 |
 |
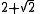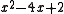3.414214... |
 |
 |
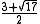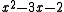3.561553... |
 |
 |
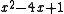3.732051... |
 |
 |
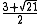3.791288... |
 |
 |
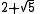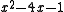4.236068... |
Powers of PV-numbers
Pisot–Vijayaraghavan numbers can be used to generate almost integers: the nth power of a Pisot number approaches integers as n approaches infinity. For example,
Since
and 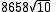differ by only 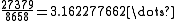is extremely close to
Indeed
Higher powers give correspondingly better rational approximations.
This property stems from the fact that for each n, the sum of nth powers of an algebraic integer x and its conjugates is exactly an integer; this follows from an application of Newton's identities
Newton's identities
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
. When x is a Pisot number, the nth powers of the other conjugates tend to 0 as n tends to infinity. Since the sum is an integer, the distance from xn to the nearest integer tends to 0 at an exponential rate.
Small Pisot numbers
All Pisot numbers that do not exceed the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
φ have been determined by Dufresnoy and Pisot. The table below lists ten smallest Pisot numbers in the increasing order. The polynomials in this table, with the exception of
are factors of either
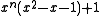
or
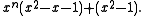
The first polynomial is divisible by x2 − 1 when n is odd and by x − 1 when n is even. It has one other real zero, which is a PV number. Dividing either polynomial by xn gives expressions that approach x2 − x − 1 as n grows very large and have zeros that converge
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to φ. A complementary pair of polynomials,
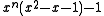
and
yields Pisot numbers that approach φ from above.
| Value | Root of... | Root of... | |
|---|---|---|---|
| 1 | 1.3247179572447460260 (plastic number Plastic number In mathematics, the plastic number ρ is a mathematical constant which is the unique real solution of the cubic equationx^3=x+1\, .... ) |
 |
 |
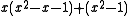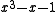| 2 | 1.3802775690976141157 |  |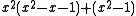
 |
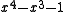| 3 | 1.4432687912703731076 |  |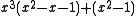
 |
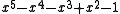| 4 | 1.4655712318767680267 |  |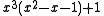
 |
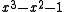| 5 | 1.5015948035390873664 |  |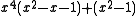
 |
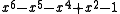| 6 | 1.5341577449142669154 |  |
 |
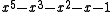| 7 | 1.5452156497327552432 |  |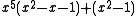
 |
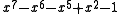| 8 | 1.5617520677202972947 |  |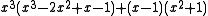
 |
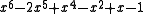| 9 | 1.5701473121960543629 |  |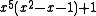
 |
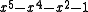| 10 | 1.5736789683935169887 |  |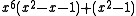
 |
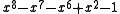Since these PV numbers are less than 2, they are all units: their minimal polynomials end in 1 or −1.
External links
- Pisot number, Encyclopedia of Mathematics