
Order type
Encyclopedia
In mathematics
, especially in set theory
, two ordered set
s X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection
f: X → Y such that both f and its inverse are monotone (order preserving). (In the special case when X is totally ordered, monotonicity of f implies monotonicity of its inverse.)
For example, the set of integers and the set of even integers have the same order type, because the mapping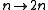 preserves the order. But the set of integers and the set of rational numbers (with the standard ordering) are not order isomorphic, because, even though the sets are of the same size (they are both countably infinite
preserves the order. But the set of integers and the set of rational numbers (with the standard ordering) are not order isomorphic, because, even though the sets are of the same size (they are both countably infinite
), there is no order-preserving bijective mapping between them. To these two order types we may add two more: the set of positive integers (which has a least element), and that of negative integers (which has a greatest element). The open interval (0,1) of rationals is order isomorphic to the rationals (since
provides a monotone bijection from the former to the latter); the half-closed intervals [0,1) and (0,1], and the closed interval [0,1], are three additional order type examples.
Since order-equivalence is an equivalence relation
, it partitions the class of all ordered sets into equivalence classes.
The order type of a well-ordered set V is sometimes expressed as ord(V).
For example, consider the set of even ordinals less than ω·2+7, which is:
Its order type is:
Because there are 2 separate lists of counting and 4 in sequence at the end.
is usually denoted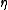 . If a set S has order type
. If a set S has order type  , the order type of the dual
, the order type of the dual
of S (the reversed order) is denoted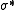 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, two ordered set
Ordered set
In order theory in mathematics, a set with a binary relation R on its elements that is reflexive , antisymmetric and transitive is described as a partially ordered set or poset...
s X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
f: X → Y such that both f and its inverse are monotone (order preserving). (In the special case when X is totally ordered, monotonicity of f implies monotonicity of its inverse.)
For example, the set of integers and the set of even integers have the same order type, because the mapping
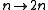 preserves the order. But the set of integers and the set of rational numbers (with the standard ordering) are not order isomorphic, because, even though the sets are of the same size (they are both countably infinite
preserves the order. But the set of integers and the set of rational numbers (with the standard ordering) are not order isomorphic, because, even though the sets are of the same size (they are both countably infiniteCountable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
), there is no order-preserving bijective mapping between them. To these two order types we may add two more: the set of positive integers (which has a least element), and that of negative integers (which has a greatest element). The open interval (0,1) of rationals is order isomorphic to the rationals (since

provides a monotone bijection from the former to the latter); the half-closed intervals [0,1) and (0,1], and the closed interval [0,1], are three additional order type examples.
Since order-equivalence is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, it partitions the class of all ordered sets into equivalence classes.
Order type of well-orderings
Every well-ordered set is order-equivalent to exactly one ordinal number. The ordinal numbers are taken to be the canonical representatives of their classes, and so the order type of a well-ordered set is usually identified with the corresponding ordinal. For example, the order type of the natural numbers is ω.The order type of a well-ordered set V is sometimes expressed as ord(V).
For example, consider the set of even ordinals less than ω·2+7, which is:
- V = {0, 2, 4, 6, ...; ω, ω+2, ω+4, ...; ω·2, ω·2+2, ω·2+4, ω·2+6}.
Its order type is:
- ord(V) = ω·2+4 = {0, 1, 2, 3, ...; ω, ω+1, ω+2, ...; ω·2, ω·2+1, ω·2+2, ω·2+3}.
Because there are 2 separate lists of counting and 4 in sequence at the end.
Rational numbers
Any countable totally ordered set can be mapped injectively into the rational numbers in an order-preserving way.Notation
The order type of the rationalsRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
is usually denoted
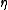 . If a set S has order type
. If a set S has order type  , the order type of the dual
, the order type of the dualDuality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
of S (the reversed order) is denoted
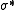 .
.

