Home Discussion Topics Dictionary Almanac

Signup Login

Parametric model

Discussion

Ask a question about 'Parametric model'

Start a new discussion about 'Parametric model'

Answer questions from other users

Full Discussion Forum

Encyclopedia

In statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, a parametric model or parametric family or finite-dimensional model is a family of distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

s that can be described using a finite number of parameter

Parameter

Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....

s. These parameters are usually collected together to form a single k-dimensional parameter vector θ = (θ₁, θ₂, …, θ_k).

Parametric models are contrasted with the semi-parametric, semi-nonparametric, and non-parametric models, all of which consist of an infinite set of “parameters” for description. The distinction between these four classes is as follows:

in a “parametric” model all the parameters are in finite-dimensional parameter spaces;
a model is “nonparametric” if all the parameters are in infinite-dimensional parameter spaces;
a “semi-parametric” model contains finite-dimensional parameters of interest and infinite-dimensional nuisance parameters;
a “semi-nonparametric” model has both finite-dimensional and infinite-dimensional unknown parameters of interest.

Some statisticians believe that the concepts “parametric”, “non-parametric”, and “semi-parametric” are ambiguous. It can also be noted that the set of all probability measures has cardinality of continuum, and therefore it is possible to parametrize any model at all by a single number in (0,1) interval. This difficulty can be avoided by considering only “smooth” parametric models.

Definition

A parametric model is a collection of probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

s such that each member of this collection, P_θ, is described by a finite-dimensional parameter θ. The set of all allowable values for the parameter is denoted Θ ⊆ R^k, and the model itself is written as

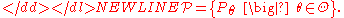
When the model consists of absolutely continuous distributions, it is often specified in terms of corresponding probability density function

Probability density function

In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

s:

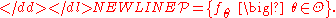
The parametric model is called identifiable if the mapping θ ↦ P_θ is invertible, that is there are no two different parameter values θ₁ and θ₂ such that P_θ₁ = P_θ₂.

Examples

The Poisson family
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...

of distributions is parametrized by a single number λ > 0:

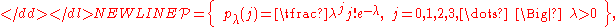
where p_λ is the probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...

. This family is an exponential family
Exponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...

.

The normal family is parametrized by θ = (μ,σ), where μ ∈ R is a location parameter, and σ > 0 is a scale parameter. This parametrized family is both an exponential family
Exponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...

and a location-scale family
Location-scale family
In probability theory, especially as that field is used in statistics, a location-scale family is a family of univariate probability distributions parametrized by a location parameter and a non-negative scale parameter; if X is any random variable whose probability distribution belongs to such a...

:

The Weibull translation model has three parameters θ = (λ, β, μ):

This model is not regular (see definition below) unless we restrict β to lie in the interval (2, +∞).

Regular parametric model

Let μ be a fixed σ-finite measure on a probability space

Probability space

In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...

(Ω, ℱ), and

the collection of all probability measures dominated by μ. Then we will call

\mathcal{P}\!=\!\{ P_\theta|\, \theta\in\Theta \} \subseteq \mathcal{M}_\mu

a regular parametric model if the following requirements are met:

Θ is an open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

of R^k.
The map

from Θ to L²(μ) is Fréchet differentiable
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...

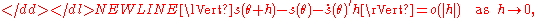
: there exists a vector $\dot{s}(\theta) = (\dot{s}_1(\theta),\,\ldots,\,\dot{s}_k(\theta))$ such that

where ′ denotes matrix transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...

.

The map $\theta\mapsto\dot{s}(\theta)$ (defined above) is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

on Θ.

The k×k Fisher information matrix

is non-singular.

Properties

Sufficient conditions for regularity of a parametric model in terms of ordinary differentiability of the density function ƒ_θ are following:
1. The density function ƒ_θ(x) is continuously differentiable in θ for μ-almost all x, with gradient ∇ƒ_θ.
2. The score function
  
  belongs to the space L²(P_θ) of square-integrable functions with respect to the measure P_θ.
  
  The Fisher information matrix I(θ), defined as
  
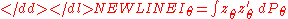
  is nonsingular and continuous in θ.
If conditions (i)−(iii) hold then the parametric model is regular.
Local asymptotic normality
Local asymptotic normality
In statistics, local asymptotic normality is a property of a sequence of statistical models, which allows this sequence to be asymptotically approximated by a normal location model, after a rescaling of the parameter...

.
If the regular parametric model is identifiable then there exists a uniformly -consistent and efficient estimator of its parameter θ.

Parametric model

Definition

Examples

Regular parametric model

Properties

See also