
Exponential family
Encyclopedia
- "Natural parameter" links here. For the usage of this term in differential geometry, see differential geometry of curvesDifferential geometry of curvesDifferential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
.
In probability and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, an exponential family is an important class of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural distributions to consider. The concept of exponential families is credited to E. J. G. Pitman
E. J. G. Pitman
Edwin James George Pitman was an Australian mathematician who made a significant contribution to statistics and probability theory...
, G. Darmois
Georges Darmois
Georges Darmois was a French mathematician and statistician. He pioneered in the theory of sufficiency, in stellar statistics, and in factor analysis...
, and B. O. Koopman
Bernard Koopman
Bernard Osgood Koopman was a French-born American mathematician, known for his work in ergodic theory, the foundations of probability, statistical theory and operations research....
in 1935–6. The term exponential class is sometimes used in place of "exponential family".
The exponential families include many of the most common distributions, including the normal, exponential
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
, gamma, chi-squared, beta, Dirichlet, Bernoulli, binomial, multinomial, Poisson
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
, Wishart, Inverse Wishart and many others. Consideration of these, and other distributions that are with an exponential family of distributions, provides a framework for selecting a possible alternative parameterisation of the distribution, in terms of natural parameters, and for defining useful sample statistics, called the natural statistics of the family. See below for more information.
Definition
The following is a sequence of increasingly general definitions of an exponential family. A casual reader may wish to restrict attention to the first and simplest definition, which corresponds to a single-parameter family of discrete or continuous probability distributions.Scalar parameter
A single-parameter exponential family is a set of probability distributions whose probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(or probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
, for the case of a discrete distribution) can be expressed in the form
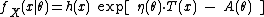
where
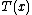 ,
, 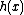 ,
, 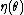 , and
, and  are known functions.
are known functions.An alternative, equivalent form often given is
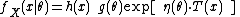
or equivalently

The value
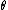 is called the parameter of the family.
is called the parameter of the family.Note that
 is often a vector of measurements, in which case
is often a vector of measurements, in which case 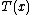 is a function from the space of possible values of
is a function from the space of possible values of  to the real numbers.
to the real numbers.If
 , then the exponential family is said to be in canonical form
, then the exponential family is said to be in canonical formCanonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
. By defining a transformed parameter
 , it is always possible to convert an exponential family to canonical form. The canonical form is non-unique, since
, it is always possible to convert an exponential family to canonical form. The canonical form is non-unique, since 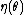 can be multiplied by any nonzero constant, provided that
can be multiplied by any nonzero constant, provided that 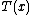 is multiplied by that constant's reciprocal.
is multiplied by that constant's reciprocal.Even when x is a scalar, and there is only a single parameter, the functions
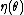 and
and 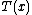 can still be vectors, as described below.
can still be vectors, as described below.Note also that the function
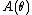 or equivalently
or equivalently 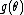 is automatically determined once the other functions have been chosen, and assumes a form that causes the distribution to be normalized (sum or integrate to one over the entire domain). Furthermore, both of these functions can always be written as functions of
is automatically determined once the other functions have been chosen, and assumes a form that causes the distribution to be normalized (sum or integrate to one over the entire domain). Furthermore, both of these functions can always be written as functions of  , even when
, even when 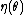 is not a one-to-one function, i.e. two or more different values of
is not a one-to-one function, i.e. two or more different values of 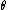 map to the same value of
map to the same value of  , and hence
, and hence  cannot be inverted. In such a case, all values of
cannot be inverted. In such a case, all values of 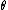 mapping to the same
mapping to the same 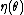 will also have the same value for
will also have the same value for  and
and 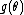 .
.Further down the page is the example of a normal distribution with unknown mean and known variance.
Factorization of the variables involved
What is important to note, and what characterizes all exponential family variants, is that the parameter(s) and the observation variable(s) must factorize (can be separated into products each of which involves only one type of variable), either directly or within either part (the base or exponent) of an exponentiationExponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
operation. Generally, this means that all of the factors constituting the density or mass function must be of one of the following forms:
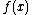 ,
, 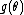 ,
, 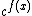 ,
, 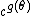 ,
,  ,
,  ,
,  ,
, 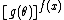 ,
, 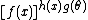 , or
, or  , where
, where  and
and 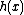 are arbitrary functions of
are arbitrary functions of  ;
; 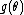 and
and  are arbitrary functions of
are arbitrary functions of 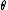 ; and
; and  is an arbitrary "constant" expression (i.e. an expression not involving
is an arbitrary "constant" expression (i.e. an expression not involving  or
or  ).
).There are further restrictions on how many such factors can occur. For example, an expression of the sort
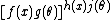 is the same as
is the same as 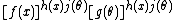 , i.e. a product of two "allowed" factors. However, when rewritten into the factorized form,
, i.e. a product of two "allowed" factors. However, when rewritten into the factorized form,
it can be seen that it cannot be expressed in the required form. (However, a form of this sort is a member of a curved exponential family, which allows multiple factorized terms in the exponent.)
To see why an expression of the form
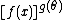 qualifies, note that
qualifies, note that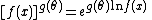
and hence factorizes inside of the exponent. Similarly,
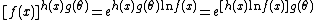
and again factorizes inside of the exponent.
Note also that a factor consisting of a sum where both types of variables are involved (e.g. a factor of the form
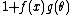 ) cannot be factorized in this fashion (except in some cases where occurring directly in an exponent); this is why, for example, the Cauchy distribution
) cannot be factorized in this fashion (except in some cases where occurring directly in an exponent); this is why, for example, the Cauchy distributionCauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
and Student's t distribution are not exponential families.
Vector parameter
The definition in terms of one real-number parameter can be extended to one real-vector parameter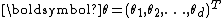 . A family of distributions is said to belong to a vector exponential family if the probability density function (or probability mass function, for discrete distributions) can be written as
. A family of distributions is said to belong to a vector exponential family if the probability density function (or probability mass function, for discrete distributions) can be written as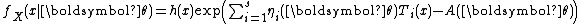
Or in a more compact form,
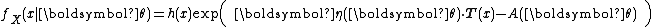
This form writes the sum as a dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of vector-valued functions
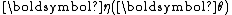 and
and 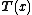 .
.An alternative, equivalent form often seen is
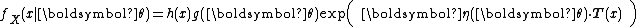
As in the scalar valued case, the exponential family is said to be in canonical form if
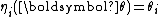 , for all
, for all 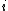 .
.A vector exponential family is said to be curved if the dimension of
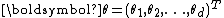 is less than the dimension of the vector
is less than the dimension of the vector 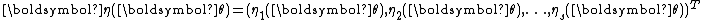 . That is, if the dimension of the parameter vector is less than the number of functions of the parameter vector in the above representation of the probability density function. Note that most common distributions in the exponential family are not curved, and many algorithms designed to work with any member of the exponential family implicitly or explicitly assume that the distribution is not curved.
. That is, if the dimension of the parameter vector is less than the number of functions of the parameter vector in the above representation of the probability density function. Note that most common distributions in the exponential family are not curved, and many algorithms designed to work with any member of the exponential family implicitly or explicitly assume that the distribution is not curved.Note that, as in the above case of a scalar-valued parameter, the function
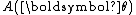 or equivalently
or equivalently 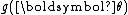 is automatically determined once the other functions have been chosen, so that the entire distribution is normalized. In addition, as above, both of these functions can always be written as functions of
is automatically determined once the other functions have been chosen, so that the entire distribution is normalized. In addition, as above, both of these functions can always be written as functions of  , regardless of the form of the transformation that generates
, regardless of the form of the transformation that generates 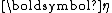 from
from  . Hence an exponential family in its "natural form" (parametrized by its natural parameter) looks like
. Hence an exponential family in its "natural form" (parametrized by its natural parameter) looks like
or equivalently
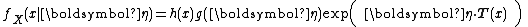
Note that the above forms may sometimes be seen with
 in place of
in place of 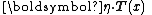 . These are exactly equivalent formulations, merely using different notation for the dot product.
. These are exactly equivalent formulations, merely using different notation for the dot product.Further down the page is the example of a normal distribution with unknown mean and variance.
Vector parameter, vector variable
The vector-parameter form over a single scalar-valued random variable can be trivially expanded to cover a joint distribution over a vector of random variables. The resulting distribution is simply the same as the above distribution for a scalar-valued random variable with each occurrence of the scalar replaced by the vector
replaced by the vector 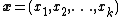 . Note that the dimension
. Note that the dimension 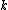 of the random variable need not match the dimension
of the random variable need not match the dimension 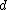 of the parameter vector, nor (in the case of a curved exponential function) the dimension
of the parameter vector, nor (in the case of a curved exponential function) the dimension  of the natural parameter
of the natural parameter 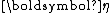 and sufficient statistic
and sufficient statistic 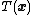 .
.The distribution in this case is written as
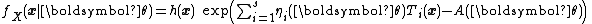
Or more compactly as
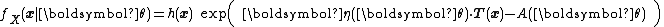
Or alternatively as

Measure-theoretic formulation
We use cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s (cdf) in order to encompass both discrete and continuous distributions.
Suppose H is a non-decreasing function of a real variable. Then Lebesgue–Stieltjes integrals with respect to dH(x) are integrals with respect to the "reference measure" of the exponential family generated by H.
Any member of that exponential family has cumulative distribution function
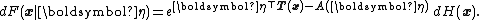
If F is a continuous distribution with a density, one can write dF(x) = f(x) dx.
H(x) is a Lebesgue–Stieltjes integrator for the reference measure. When the reference measure is finite, it can be normalized and H is actually the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of a probability distribution. If F is absolutely continuous with a density, then so is H, which can then be written dH(x) = h(x) dx. If F is discrete, then H is a step function
Step function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...
(with steps on the support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of F).
Interpretation
In the definitions above, the functions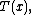
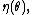 and
and 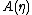 were apparently arbitrarily defined. However, these functions play a significant role in the resulting probability distribution.
were apparently arbitrarily defined. However, these functions play a significant role in the resulting probability distribution.-
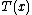 is a sufficient statisticSufficiency (statistics)In statistics, a sufficient statistic is a statistic which has the property of sufficiency with respect to a statistical model and its associated unknown parameter, meaning that "no other statistic which can be calculated from the same sample provides any additional information as to the value of...
is a sufficient statisticSufficiency (statistics)In statistics, a sufficient statistic is a statistic which has the property of sufficiency with respect to a statistical model and its associated unknown parameter, meaning that "no other statistic which can be calculated from the same sample provides any additional information as to the value of...
of the distribution. Thus, for exponential families, there exists a sufficient statistic whose dimension equals the number of parameters to be estimated. This important property is further discussed below.
-
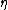 is called the natural parameter. The set of values of
is called the natural parameter. The set of values of 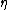 for which the function
for which the function 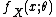 is finite is called the natural parameter space. It can be shown that the natural parameter space is always convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
is finite is called the natural parameter space. It can be shown that the natural parameter space is always convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
.
-
 is a normalization factor, or log-partition functionPartition function (mathematics)The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
is a normalization factor, or log-partition functionPartition function (mathematics)The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
, without which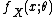 would not be a probability distribution. The function A is important in its own right, because K(u|η) = A(η + u) − A(η) is the cumulant generating function of the sufficient statistic T(x). This means one can fully understand the mean and covariance structure of T = (T1, T2, ... , Tp) by differentiating
would not be a probability distribution. The function A is important in its own right, because K(u|η) = A(η + u) − A(η) is the cumulant generating function of the sufficient statistic T(x). This means one can fully understand the mean and covariance structure of T = (T1, T2, ... , Tp) by differentiating 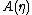 .
.
Examples
The normal, exponentialExponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
, gamma, chi-squared, beta, Weibull (with known parameter k), Dirichlet, Bernoulli, binomial, multinomial, Poisson
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
, negative binomial
Negative binomial distribution
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
(with known parameter r), and geometric distributions are all exponential families. The family of Pareto distributions with a fixed minimum bound form an exponential family.
The Cauchy
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
and uniform
Uniform distribution
-Probability theory:* Discrete uniform distribution* Continuous uniform distribution-Other:* "Uniform distribution modulo 1", see Equidistributed sequence*Uniform distribution , a type of species distribution* Distribution of military uniforms...
families of distributions are not exponential families. The Laplace family is not an exponential family unless the mean is zero.
Following are some detailed examples of the representation of some useful distribution as exponential families.
Normal distribution: Unknown mean, known variance
As a first example, consider a random variable distributed normally with unknown mean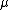 and known variance
and known variance 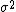 . The probability density function is then
. The probability density function is then
This is a single-parameter exponential family, as can be seen by setting
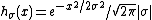
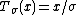
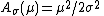
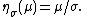
If σ = 1 this is in canonical form, as then η(μ) = μ.
Normal distribution: Unknown mean and unknown variance
Next, consider the case of a normal distribution with unknown mean and unknown variance. The probability density function is then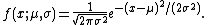
This is an exponential family which can be written in canonical form by defining
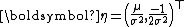
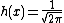
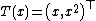
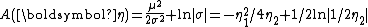
Binomial distribution
As an example of a discrete exponential family, consider the binomial distribution with known number of trials n. The probability mass functionProbability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
for this distribution is
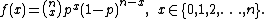
This can equivalently be written as

which shows that the binomial distribution is an exponential family, whose natural parameter is
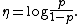
This function of p is known as logit
Logit
The logit function is the inverse of the sigmoidal "logistic" function used in mathematics, especially in statistics.Log-odds and logit are synonyms.-Definition:The logit of a number p between 0 and 1 is given by the formula:...
.
Normalization of the distribution
We start with the normalization of the probability distribution. Since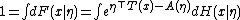
it follows that
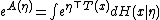
This justifies calling A the log-partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
.
Moment generating function of the sufficient statistic
Now, the moment generating function of T(x) is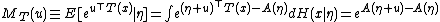
proving the earlier statement that
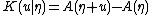 is the cumulant generating function for T.
is the cumulant generating function for T.An important subclass of the exponential family the natural exponential family
Natural exponential family
In probability and statistics, the natural exponential family is a class of probability distributions that is a special case of an exponential family...
has a similar form for the moment generating function for the distribution of x.
Differential identities for cumulants
In particular,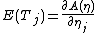
and
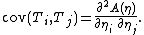
The first two raw moments and all mixed second moments can be recovered from these two identities. Higher order moments and cumulants are obtained by higher derivatives. This technique is often useful when T is a complicated function of the data, whose moments are difficult to calculate by integration.
Example
As an example consider a real valued random variable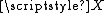 with density
with density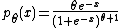
indexed by shape parameter
 (this is called the skew-logistic distribution). The density can be rewritten as
(this is called the skew-logistic distribution). The density can be rewritten as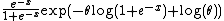
Notice this is an exponential family with natural parameter
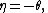
sufficient statistic
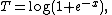
and normalizing factor
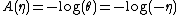
So using the first identity,
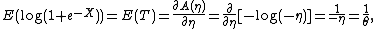
and using the second identity
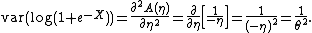
This example illustrates a case where using this method is very simple, but the direct calculation would be nearly impossible.
Maximum entropy derivation
The exponential family arises naturally as the answer to the following question: what is the maximum-entropyPrinciple of maximum entropy
In Bayesian probability, the principle of maximum entropy is a postulate which states that, subject to known constraints , the probability distribution which best represents the current state of knowledge is the one with largest entropy.Let some testable information about a probability distribution...
distribution consistent with given constraints on expected values?
The information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
of a probability distribution dF(x) can only be computed with respect to some other probability distribution (or, more generally, a positive measure), and both measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
s must be mutually absolutely continuous. Accordingly, we need to pick a reference measure dH(x) with the same support as dF(x). As an aside, frequentists
Frequency probability
Frequency probability is the interpretation of probability that defines an event's probability as the limit of its relative frequency in a large number of trials. The development of the frequentist account was motivated by the problems and paradoxes of the previously dominant viewpoint, the...
need to realize that this is a largely arbitrary choice, while Bayesians
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
can just make this choice part of their prior probability distribution.
The entropy of dF(x) relative to dH(x) is
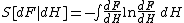
or
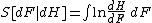
where dF/dH and dH/dF are Radon–Nikodym derivatives. Note that the ordinary definition of entropy for a discrete distribution supported on a set I, namely

assumes, though this is seldom pointed out, that dH is chosen to be the counting measure
Counting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
on I.
Consider now a collection of observable quantities (random variables) Ti. The probability distribution dF whose entropy with respect to dH is greatest, subject to the conditions that the expected value of Ti be equal to ti, is a member of the exponential family with dH as reference measure and (T1, ..., Tn) as sufficient statistic.
The derivation is a simple variational calculation
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
using Lagrange multipliers
Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
. Normalization is imposed by letting T0 = 1 be one of the constraints. The natural parameters of the distribution are the Lagrange multipliers, and the normalization factor is the Lagrange multiplier associated to T0.
For examples of such derivations, see Maximum entropy probability distribution
Maximum entropy probability distribution
In statistics and information theory, a maximum entropy probability distribution is a probability distribution whose entropy is at least as great as that of all other members of a specified class of distributions....
.
Classical estimation: sufficiency
According to the PitmanE. J. G. Pitman
Edwin James George Pitman was an Australian mathematician who made a significant contribution to statistics and probability theory...
–Koopman
Bernard Koopman
Bernard Osgood Koopman was a French-born American mathematician, known for his work in ergodic theory, the foundations of probability, statistical theory and operations research....
–Darmois
Georges Darmois
Georges Darmois was a French mathematician and statistician. He pioneered in the theory of sufficiency, in stellar statistics, and in factor analysis...
theorem, among families of probability distributions whose domain does not vary with the parameter being estimated, only in exponential families is there a sufficient statistic whose dimension remains bounded as sample size increases. Less tersely, suppose Xn, n = 1, 2, 3, ... are independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
identically distributed random variables whose distribution is known to be in some family of probability distributions. Only if that family is an exponential family is there a (possibly vector-valued) sufficient statistic T(X1, ..., Xn) whose number of scalar components does not increase as the sample size n increases.
Bayesian estimation: conjugate distributions
Exponential families are also important in Bayesian statisticsBayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
. In Bayesian statistics a prior distribution is multiplied by a likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
and then normalised to produce a posterior distribution. In the case of a likelihood which belongs to the exponential family there exists a conjugate prior
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
, which is often also in the exponential family. A conjugate prior
 for the parameter
for the parameter 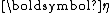 of an exponential family is given by
of an exponential family is given by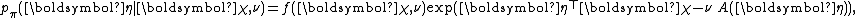
or equivalently
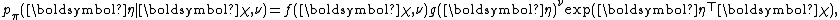
where
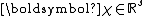 (where
(where  is the dimension of
is the dimension of  ) and
) and 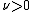 are hyperparameter
are hyperparameterHyperparameter
In Bayesian statistics, a hyperparameter is a parameter of a prior distribution; the term is used to distinguish them from parameters of the model for the underlying system under analysis...
s (parameters controlling parameters).
 corresponds to the effective number of observations that the prior distribution contributes, and
corresponds to the effective number of observations that the prior distribution contributes, and 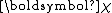 corresponds to the total amount that these pseudo-observations contribute to the sufficient statistic over all observations and pseudo-observations.
corresponds to the total amount that these pseudo-observations contribute to the sufficient statistic over all observations and pseudo-observations. 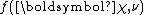 is a normalization constant that is automatically determined by the remaining functions and serves to ensure that the given function is a probability density function
is a normalization constant that is automatically determined by the remaining functions and serves to ensure that the given function is a probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(i.e. it is normalized).
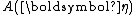 and equivalently
and equivalently 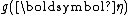 are the same functions as in the definition of the distribution over which
are the same functions as in the definition of the distribution over which  is the conjugate prior.
is the conjugate prior.A conjugate prior is one which, when combined with the likelihood and normalised, produces a posterior distribution which is of the same type as the prior. For example, if one is estimating the success probability of a binomial distribution, then if one chooses to use a beta distribution as one's prior, the posterior is another beta distribution. This makes the computation of the posterior particularly simple. Similarly, if one is estimating the parameter of a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
the use of a gamma prior will lead to another gamma posterior. Conjugate priors are often very flexible and can be very convenient. However, if one's belief about the likely value of the theta parameter of a binomial is represented by (say) a bimodal (two-humped) prior distribution, then this cannot be represented by a beta distribution. It can however be represented by using a mixture density
Mixture density
In probability and statistics, a mixture distribution is the probability distribution of a random variable whose values can be interpreted as being derived in a simple way from an underlying set of other random variables. In particular, the final outcome value is selected at random from among the...
as the prior, here a combination of two beta distributions; this is a form of hyperprior
Hyperprior
In Bayesian statistics, a hyperprior is a prior distribution on a hyperparameter, that is, on a parameter of a prior distribution.As with the term hyperparameter, the use of hyper is to distinguish it from a prior distribution of a parameter of the model for the underlying system...
.
An arbitrary likelihood will not belong to the exponential family, and thus in general no conjugate prior exists. The posterior will then have to be computed by numerical methods.
Hypothesis testing: Uniformly most powerful tests
The one-parameter exponential family has a monotone non-decreasing likelihood ratio in the sufficient statisticSufficiency (statistics)
In statistics, a sufficient statistic is a statistic which has the property of sufficiency with respect to a statistical model and its associated unknown parameter, meaning that "no other statistic which can be calculated from the same sample provides any additional information as to the value of...
T(x), provided that η(θ) is non-decreasing. As a consequence, there exists a uniformly most powerful test
Uniformly most powerful test
In statistical hypothesis testing, a uniformly most powerful test is a hypothesis test which has the greatest power 1 − β among all possible tests of a given size α...
for testing the hypothesis H0: θ ≥ θ0 vs. H1: θ < θ0.
Generalized linear models
The exponential family forms the basis for the distribution function used in generalized linear models, a class of model that encompass many of the commonly used regression models in statistics.See also
- Natural exponential familyNatural exponential familyIn probability and statistics, the natural exponential family is a class of probability distributions that is a special case of an exponential family...
- Exponential dispersion modelExponential dispersion modelExponential dispersion models are statistical models in which the probability distribution is of a special form. This class of models represents a generalisation of the exponential family of models which themselves play an important role in statistical theory because they have a special structure...
- Gibbs measureGibbs measureIn mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...

