Overdetermined system
Encyclopedia
In mathematics
, a system of linear equations is considered overdetermined if there are more equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown
can be seen as an available degree of freedom
. Each equation introduced into the system can be viewed as a constraint that restricts one degree of freedom.
Therefore the critical case occurs when the number of equations and the number of independent variables are equal. For every degree of freedom, there exists a corresponding restraint. The overdetermined case occurs when the system has been overconstrained—that is, when the number of equations outnumbers the number of the unknowns.
s and 2 unknowns (x1 and x2):
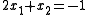
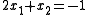
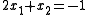
Note: equations above correspond to picture #1 such that x1 = x and x2 = y in the Cartesian coordinate plane
There are three "solutions" to the system as can be determined from the graph's intersections, one for each pair of linear equations: between one and two (0.2, −1.4), between one and three (−2/3, 1/3), between two and three (1.5, 2.5). However there is no solution that satisfies all three simultaneously. Systems of this variety are deemed inconsistent.
The only case where the overdetermined system does in fact have a solution is demonstrated in pictures four, five, and six. These exceptions occur when the overdetermined set contains linearly dependent equations. Linear dependence means that the elements of a set can be described in terms of existing equations. For example, y = x + 1 and 2y = 2x + 2 are linearly dependent equations.
equation.
The previous system of equations can be written as follows: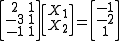
Notice that the number of rows outnumber the number of columns. In linear algebra
the concepts of row space
, column space
and null space
are important for determining the properties of matrices. The informal discussion of constraints and degrees of freedom
above relate directly to these more formal concepts.
solution, or the trivial solution plus an infinite set of solutions, of nature determined by the number of linearly dependent equations.
Consider the system of linear equations: Li = 0 for 1 ≤ i ≤ M, and variables X1, X2, ..., XN, then X1 = X2 = ... = XN = 0 is always a solution. When M < N the system is underdetermined and there are always further solutions. In fact the dimension of the space of solutions is always at least N − M.
For M ≥ N, there may be no solution other than all values being 0. There will be other solutions just when the system of equations has enough dependencies (linearly dependent elements), so that the number of effective constraints is less than the apparent number M; more precisely the system must reduce to at most N − 1 equations. All we can be sure about is that it will reduce to at most N.
) lead to three possible cases for an overdetermined system.
Note:(*Equations and unknowns can correspond to the rows and columns of a matrix respectively)
The discussion is more convincing, perhaps, when translated into the geometric language of intersecting hyperplane
s. The homogeneous case applies to hyperplanes through a given point, taken as origin of coordinates. The inhomogeneous case is for general hyperplanes, which may therefore exhibit parallelism or intersect. A sequence of hyperplanes H1, H2, ..., HM gives rise to intersections of the first k, which are expected to drop in dimension 1 each time. If M > N, the dimension of the ambient space, we expect the intersection to be empty
, and this is precisely the overdetermined case.
can be used to find an approximate solution to overdetermined systems. For the system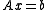
, the least squares formula can be written
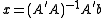with this formula an approximate solution is found.
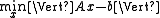
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a system of linear equations is considered overdetermined if there are more equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
can be seen as an available degree of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
. Each equation introduced into the system can be viewed as a constraint that restricts one degree of freedom.
Therefore the critical case occurs when the number of equations and the number of independent variables are equal. For every degree of freedom, there exists a corresponding restraint. The overdetermined case occurs when the system has been overconstrained—that is, when the number of equations outnumbers the number of the unknowns.
An example in two dimensions
Consider the system of 3 equationEquation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s and 2 unknowns (x1 and x2):
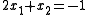
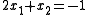
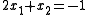
Note: equations above correspond to picture #1 such that x1 = x and x2 = y in the Cartesian coordinate plane
There are three "solutions" to the system as can be determined from the graph's intersections, one for each pair of linear equations: between one and two (0.2, −1.4), between one and three (−2/3, 1/3), between two and three (1.5, 2.5). However there is no solution that satisfies all three simultaneously. Systems of this variety are deemed inconsistent.
The only case where the overdetermined system does in fact have a solution is demonstrated in pictures four, five, and six. These exceptions occur when the overdetermined set contains linearly dependent equations. Linear dependence means that the elements of a set can be described in terms of existing equations. For example, y = x + 1 and 2y = 2x + 2 are linearly dependent equations.
Matrix form
Any system of linear equations can be written as a matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
equation.
The previous system of equations can be written as follows:
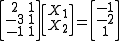
Notice that the number of rows outnumber the number of columns. In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
the concepts of row space
Row space
In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...
, column space
Column space
In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
and null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
are important for determining the properties of matrices. The informal discussion of constraints and degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
above relate directly to these more formal concepts.
Homogeneous case
The homogeneous case is always consistent (because there is a trivial, all-zero solution). There are two cases, in rough terms: there is just the trivialTrivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
solution, or the trivial solution plus an infinite set of solutions, of nature determined by the number of linearly dependent equations.
Consider the system of linear equations: Li = 0 for 1 ≤ i ≤ M, and variables X1, X2, ..., XN, then X1 = X2 = ... = XN = 0 is always a solution. When M < N the system is underdetermined and there are always further solutions. In fact the dimension of the space of solutions is always at least N − M.
For M ≥ N, there may be no solution other than all values being 0. There will be other solutions just when the system of equations has enough dependencies (linearly dependent elements), so that the number of effective constraints is less than the apparent number M; more precisely the system must reduce to at most N − 1 equations. All we can be sure about is that it will reduce to at most N.
Inhomogeneous case
When studying systems of linear equations, Li=ci for 1 ≤ i ≤ M, in variables X1, X2, ..., XN the equations Li are sometimes linearly dependent. These dependent equations (often described in terms of vectorsCoordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
) lead to three possible cases for an overdetermined system.
- M equations* and N unknowns*, such that M > N and all M are linearly independent. This case yields no solution.
- M equations and N unknowns, such that M > N but all M are not linearly independent. There exist three possible sub-cases of this:
- M equations and N unknowns, such that M > N but all M are not linearly independent, but when the linearly dependent equations(D) are removed M - D > N. This case yields no solutions.
- M equations and N unknowns, such that M > N but all M are not linearly independent, but when the linearly dependent equations(D) are removed M - D = N. This case yields a single solution.
- M equations and N unknowns, such that M > N but all M are not linearly independent, but when the linearly dependent equations(D) are removed M - D < N. This case yields infinitely many solutions. Which can be described as F which is the entirety of the field in which the equations are operating.
Note:(*Equations and unknowns can correspond to the rows and columns of a matrix respectively)
- M equations and N unknowns, such that M < N and all M are linearly dependent. This case yields infinitely many solutions except in some cases where the solution is sparse (see Compressed SensingCompressed sensingCompressed sensing, also known as compressive sensing, compressive sampling and sparse sampling, is a technique for finding sparse solutions to underdetermined linear systems...
)
The discussion is more convincing, perhaps, when translated into the geometric language of intersecting hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s. The homogeneous case applies to hyperplanes through a given point, taken as origin of coordinates. The inhomogeneous case is for general hyperplanes, which may therefore exhibit parallelism or intersect. A sequence of hyperplanes H1, H2, ..., HM gives rise to intersections of the first k, which are expected to drop in dimension 1 each time. If M > N, the dimension of the ambient space, we expect the intersection to be empty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, and this is precisely the overdetermined case.
Approximate solutions
The method of least squaresLinear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
can be used to find an approximate solution to overdetermined systems. For the system
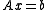, the least squares formula can be written 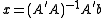with this formula an approximate solution is found.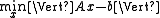In general use
The concept can also be applied to more general systems of equations, such as partial differential equations.See also
- Underdetermined systemUnderdetermined systemIn mathematics, a system of linear equations is considered underdetermined if there are fewer equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
- Frobenius theorem (differential topology)Frobenius theorem (differential topology)In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
- Integrability condition
- Least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
- Consistency proofConsistency proofIn logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
- Compressed sensingCompressed sensingCompressed sensing, also known as compressive sensing, compressive sampling and sparse sampling, is a technique for finding sparse solutions to underdetermined linear systems...
- Moore–Penrose pseudoinverse