Nowhere dense set

In mathematics, a nowhere dense set in a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 is a set whose closure

Closure (topology)

In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...

 has empty interior

Interior (topology)

In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....

. The order of operations is important. For example, the set of rational number

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

s, as a subset of R has the property that the closure of the interior is empty, but it is not nowhere dense; in fact it is dense in R.

The surrounding space matters: a set A may be nowhere dense when considered as a subspace of a topological space X but not when considered as a subspace of another topological space Y. A nowhere dense set is always dense in itself.

Every subset of a nowhere dense set is nowhere dense, and the union

Union (set theory)

In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...

 of finitely many nowhere dense sets is nowhere dense. That is, the nowhere dense sets form an ideal of sets, a suitable notion of negligible set

Negligible set

In mathematics, a negligible set is a set that is small enough that it can be ignored for some purpose.As common examples, finite sets can be ignored when studying the limit of a sequence, and null sets can be ignored when studying the integral of a measurable function.Negligible sets define...

. The union of countably many nowhere dense sets, however, need not be nowhere dense. (Thus, the nowhere dense sets need not form a sigma-ideal

Sigma-ideal

In mathematics, particularly measure theory, a σ-ideal of a sigma-algebra is a subset with certain desirable closure properties. It is a special type of ideal. Its most frequent application is perhaps in probability theory.Let be a measurable space...

.) Instead, such a union is called a meagre set

Meagre set

In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...

or a set of first category. The concept is important to formulate the Baire category theorem

Baire category theorem

The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....

.

Open and closed

• A nowhere dense set need not be closed
  Closed set
  In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
  
   (for instance, the set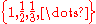 is nowhere dense in the reals), but is properly contained in a nowhere dense closed set, namely its closure
  Closure (topology)
  In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
  
   (which would add 0 to the set). Indeed, a set is nowhere dense if and only if its closure is nowhere dense.

• The complement
  Complement (set theory)
  In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
  
   of a closed nowhere dense set is a dense open set
  Open set
  The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
  
  , and thus the complement of a nowhere dense set is a set with dense interior
  Interior (topology)
  In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
  
  .

• The boundary
  Boundary (topology)
  In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
  
   of every open set is closed and nowhere dense.

• Every closed nowhere dense set is the boundary of an open set.

Nowhere dense sets with positive measure

A nowhere dense set is not necessarily negligible in every sense. For example, if X is the unit interval

Unit interval

In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...

 [0,1], not only is it possible to have a dense set of Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

 zero (such as the set of rationals), but it is also possible to have a nowhere dense set with positive measure.

For one example (a variant of the Cantor set

Cantor set

In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....

), remove from [0,1] all dyadic fractions, i.e. fractions of the form a/2ⁿ in lowest terms for positive integers a and n, and the intervals around them: [a/2ⁿ − 1/2²ⁿ⁺¹, a/2ⁿ + 1/2²ⁿ⁺¹]. Since for each n this removes intervals adding up to at most 1/2ⁿ⁺¹, the nowhere dense set remaining after all such intervals have been removed, has measure of at least 1/2 (in fact just over 0.535... because of overlaps) and so in a sense represents the majority of the ambient space [0,1].

Generalizing this method, one can construct in the unit interval nowhere dense sets of any measure less than 1.

External links

• Some nowhere dense sets with positive measure