Oded Schramm
Encyclopedia
Oded Schramm was an Israel
i-American
mathematician
known for the invention of the Schramm–Loewner evolution (SLE) and for working at the intersection of conformal field theory
and probability theory
.
. His father, Michael Schramm, was a biochemistry professor at the Hebrew University of Jerusalem.
He attended Hebrew University where he received his bachelor’s degree in mathematics and computer science in 1986 and his master's degree
in 1987, under the supervision of Gil Kalai
. He then received his Ph.D.
from Princeton University
in 1990 under the supervision of William Thurston
.
After receiving his doctorate, he worked for two years at the University of California, San Diego
, and then had a permanent position at the Weizmann Institute from 1992 to 1999. In 1999 he moved to the Theory Group at Microsoft Research
in Redmond, Washington
, where he remained for the rest of his life.
He and his wife had two children.
On September 1, 2008, Schramm fell to his death while scrambling
Guye Peak
, north of Snoqualmie Pass
in Washington.
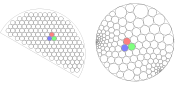A constant theme in Schramm's research was the exploration of relations between discrete models and their continuous scaling limits, which for a number of models turn out to be conformally invariant.
Schramm's most significant contribution is the invention of Schramm–Loewner evolution, a tool which has paved the way for mathematical proofs of conjectured scaling limit relations on models from statistical mechanics
such as self-avoiding random walk
and percolation
. This technique has had a profound impact on the field. It has been recognized by many awards to Schramm and others, including a Fields Medal
to Wendelin Werner
, who was one of Schramm's principal collaborators, along with Gregory Lawler. The New York Times wrote in his obituary:
Schramm's doctorate was in complex analysis
, but he made contributions in many other areas of pure mathematics, although self-taught in those areas. Frequently he would prove a result by himself before reading the literature to obtain an appropriate credit. Often his proof was original or more elegant than the original.
Besides conformally invariant planar processes and SLE, he made fundamental contributions to several topics:
Israel
The State of Israel is a parliamentary republic located in the Middle East, along the eastern shore of the Mediterranean Sea...
i-American
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
known for the invention of the Schramm–Loewner evolution (SLE) and for working at the intersection of conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
.
Biography
Schramm was born in Jerusalem in IsraelIsrael
The State of Israel is a parliamentary republic located in the Middle East, along the eastern shore of the Mediterranean Sea...
. His father, Michael Schramm, was a biochemistry professor at the Hebrew University of Jerusalem.
He attended Hebrew University where he received his bachelor’s degree in mathematics and computer science in 1986 and his master's degree
Master's degree
A master's is an academic degree granted to individuals who have undergone study demonstrating a mastery or high-order overview of a specific field of study or area of professional practice...
in 1987, under the supervision of Gil Kalai
Gil Kalai
Gil Kalai is the Henry and Manya Noskwith Professor of Mathematics at the Hebrew University of Jerusalem, and adjunct professor of mathematics and of computer science at Yale University, and the editor of the Israel Journal of Mathematics.-Biography:...
. He then received his Ph.D.
Ph.D.
A Ph.D. is a Doctor of Philosophy, an academic degree.Ph.D. may also refer to:* Ph.D. , a 1980s British group*Piled Higher and Deeper, a web comic strip*PhD: Phantasy Degree, a Korean comic series* PhD Docbook renderer, an XML renderer...
from Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
in 1990 under the supervision of William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
.
After receiving his doctorate, he worked for two years at the University of California, San Diego
University of California, San Diego
The University of California, San Diego, commonly known as UCSD or UC San Diego, is a public research university located in the La Jolla neighborhood of San Diego, California, United States...
, and then had a permanent position at the Weizmann Institute from 1992 to 1999. In 1999 he moved to the Theory Group at Microsoft Research
Microsoft Research
Microsoft Research is the research division of Microsoft created in 1991 for developing various computer science ideas and integrating them into Microsoft products. It currently employs Turing Award winners C.A.R. Hoare, Butler Lampson, and Charles P...
in Redmond, Washington
Redmond, Washington
Redmond is a city in King County, Washington, United States, located east of Seattle. The population was 54,144 at the 2010 census,up from 45,256 in 2000....
, where he remained for the rest of his life.
He and his wife had two children.
On September 1, 2008, Schramm fell to his death while scrambling
Scrambling
Scrambling is a method of ascending rocky faces and ridges. It is an ambiguous term that lies somewhere between hillwalking and rock climbing. It is often distinguished from hillwalking by defining a scramble as a route where hands must be used in the ascent...
Guye Peak
Guye Peak
Guye Peak is a mountain in Washington State, United States. Named for Francis M. Guye, who held an iron mining claim on it in the 1880s, it lies in the Alpine Lakes Wilderness area of the Cascade Range and overlooks Snoqualmie Pass from the north....
, north of Snoqualmie Pass
Snoqualmie Pass
Snoqualmie Pass is a mountain pass that carries Interstate 90 through the Cascade Range in the U.S. State of Washington. The elevation of the pass summit is , and is on the county line between Kittitas County and King County...
in Washington.
Research
Schramm's most significant contribution is the invention of Schramm–Loewner evolution, a tool which has paved the way for mathematical proofs of conjectured scaling limit relations on models from statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
such as self-avoiding random walk
Self-avoiding walk
In mathematics, a self-avoiding walk is a sequence of moves on a lattice that does not visit the same point more than once. A self-avoiding polygon is a closed self-avoiding walk on a lattice...
and percolation
Percolation
In physics, chemistry and materials science, percolation concerns the movement and filtering of fluids through porous materials...
. This technique has had a profound impact on the field. It has been recognized by many awards to Schramm and others, including a Fields Medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
to Wendelin Werner
Wendelin Werner
Wendelin Werner is a German-born French mathematician working in the area of self-avoiding random walks, Schramm-Loewner evolution, and related theories in probability theory and mathematical physics. In 2006, at the 25th International Congress of Mathematicians in Madrid, Spain he received the...
, who was one of Schramm's principal collaborators, along with Gregory Lawler. The New York Times wrote in his obituary:
Schramm's doctorate was in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, but he made contributions in many other areas of pure mathematics, although self-taught in those areas. Frequently he would prove a result by himself before reading the literature to obtain an appropriate credit. Often his proof was original or more elegant than the original.
Besides conformally invariant planar processes and SLE, he made fundamental contributions to several topics:
- Circle packingCircle packingIn geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that all circles touch another. The associated "packing density", η of an arrangement is the proportion of the surface covered by the circles...
s and discrete conformal geometryConformal geometryIn mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
. - Embeddings of Gromov hyperbolic spaces.
- PercolationPercolation theoryIn mathematics, percolation theory describes the behavior of connected clusters in a random graph. The applications of percolation theory to materials science and other domains are discussed in the article percolation.-Introduction:...
, uniform and minimal spanning trees and forests, harmonic functionHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s on Cayley graphCayley graphIn mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
s of infinite finitely generated groups (especially non-amenable groupsAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
) and the hyperbolic planeHyperbolic geometryIn mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. - Limits of sequences of finite graphsGraph (mathematics)In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. - Noise sensitivity of Boolean functions, with applications to dynamical percolation.
- Random turn games (e.g. random turn hexHex (board game)Hex is a board game played on a hexagonal grid, theoretically of any size and several possible shapes, but traditionally as an 11x11 rhombus. Other popular dimensions are 13x13 and 19x19 as a result of the game's relationship to the older game of Go...
) and the infinity LaplacianInfinity LaplacianIn mathematics, the infinity Laplace operator is a 2nd-order partial differential operator, commonly abbreviated \Delta_\infty...
equation. - Random permutationRandom permutationA random permutation is a random ordering of a set of objects, that is, a permutation-valued random variable. The use of random permutations is often fundamental to fields that use randomized algorithms such as coding theory, cryptography, and simulation...
s.
Awards and honors
- Erdős PrizeErdős Prize- References :*...
(1996) - Salem PrizeSalem PrizeThe Salem Prize, founded by the widow of Raphael Salem, is awarded every year to a young mathematician judged to have done outstanding work in Salem's field of interest, primarily the theory of Fourier series.-Past winners:...
(2001) - Clay Research AwardClay Research AwardThe Clay Research Award is given annually by the Clay Mathematics Institute to mathematicians to recognize their achievement in mathematical research...
(2002), for his work in combining analytic power with geometric insight in the field of random walks, percolation, and probability theory in general, especially for formulating stochastic Loewner evolution. His work opens new doors and reinvigorates research in these fields. - Loève PrizeLoève PrizeThe Line and Michel Loève International Prize in Probability was created in 1992 in honor of Michel Loève by his widow Line. The prize, awarded every two years, is intended to recognize outstanding contributions by researchers in mathematical probability who are under 45 years old...
(2003) - Henri Poincaré PrizePoincaré PrizeThe Henri Poincaré Prize sponsored by the Daniel Iagolnitzer Foundation was created in 1997 to recognize outstanding contributions in mathematical physics, and contributions which lay the groundwork for novel developments in this broad field...
(2003), For his contributions to discrete conformal geometry, where he discovered new classes of circle patterns described by integrable systems and proved the ultimate results on convergence to the corresponding conformal mappings, and for the discovery of the Stochastic Loewner Process as a candidate for scaling limits in two dimensional statistical mechanics. - SIAM George Pólya PrizePólya Prize (SIAM)The Pólya Prize is a prize in mathematics, awarded by the Society for Industrial and Applied Mathematics. First given in 1969, the prize is named after Hungarian mathematician George Pólya...
(2006), with Gregory Lawler and Wendelin WernerWendelin WernerWendelin Werner is a German-born French mathematician working in the area of self-avoiding random walks, Schramm-Loewner evolution, and related theories in probability theory and mathematical physics. In 2006, at the 25th International Congress of Mathematicians in Madrid, Spain he received the...
, for groundbreaking work on the development and application of stochastic Loewner evolution (SLE). Of particular note is the rigorous establishment of the existence and conformal invariance of critical scaling limits of a number of 2D lattice models arising in statistical physics. - Ostrowski PrizeOstrowski PrizeThe Ostrowski Prize is a mathematics award given every other year by an international jury from the universities of Basel, Jerusalem, Waterloo and the academies of Denmark and the Netherlands...
(2007) - Elected in 2008 as a foreign member of the Royal Swedish Academy of SciencesRoyal Swedish Academy of SciencesThe Royal Swedish Academy of Sciences or Kungliga Vetenskapsakademien is one of the Royal Academies of Sweden. The Academy is an independent, non-governmental scientific organization which acts to promote the sciences, primarily the natural sciences and mathematics.The Academy was founded on 2...
.
External links
- Tutorial: SLE, video of MSRI lecture given jointly by Schramm, Lawler and Werner in the special session at the Lawrence Hall of ScienceLawrence Hall of ScienceThe Lawrence Hall of Science is a public science center featuring hands-on exhibits and activities. Located in the hills above the University of California, Berkeley campus, LHS is also a resource center for preschool through high school science and mathematics education.Established in 1968 in...
, University of California, BerkeleyUniversity of California, BerkeleyThe University of California, Berkeley , is a teaching and research university established in 1868 and located in Berkeley, California, USA...
in May 2001. - Conformally Invariant Scaling Limits and SLE, MSRI presentation by Oded Schramm, May 2001.
- Terence TaoTerence TaoTerence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
, "Oded Schramm". - Publication list
- Oded Schramm Memorial page
- Oded Schramm Memorial blog
- Oded Schramm Memorial Workshop – August 30–31, 2009 at Microsoft Research
- Oded Schramm obituary in the IMS Bulletin