
Octonion algebra
Encyclopedia
In mathematics
, an octonion algebra over a field
F is an algebraic structure
which is an 8-dimensional
composition algebra
over F. In other words, it is a unital nonassociative algebra A over F with a nondegenerate
quadratic form
N (called the norm form) such that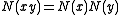
for all x and y in A.
The most well-known example of an octonion algebra are the classical octonion
s, which are an octonion algebra over R, the field of real number
s. The split-octonion
s also form an octonion algebra over R. Up to R-algebra isomorphism
, these are the only octonion algebras over the reals.
A split octonion algebra is one for which the quadratic form N is isotropic
(i.e. there exists a vector x with N(x) = 0). Up to F-algebra isomorphism, there is a unique split octonion algebra over any field F. When F is algebraically closed
or a finite field
, these are the only octonion algebras over F.
Octonion algebras are always nonassociative. They are however alternative algebra
s (a weaker form of associativity). Moreover, the Moufang identities hold in any octonion algebra. It follows that the set of invertible elements in any octonion algebra form a Moufang loop
, as do the subset of unit norm elements.
that the F-isomorphism classes of the norm form are in one-to-one correspondence with the isomorphism classes of octonion F-algebras. Moreover, the possible norm forms are exactly the Pfister 3-forms
over F.
Since any two octonion F-algebras become isomorphic over the algebraic closure of F, one can apply the ideas of non-abelian Galois cohomology
. In particular, by using the fact that the automorphism group of the split octonions is the split algebraic group
G2, one sees the correspondence of isomorphism classes of octonion F-algebras with isomorphism classes of G2-torsors over F. These isomorphism classes form the non-abelian Galois cohomology set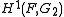 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an octonion algebra over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
which is an 8-dimensional
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
composition algebra
Composition algebra
In mathematics, a composition algebra A over a field K is a unital algebra over K together with a nondegenerate quadratic form N which satisfiesN = NN\,...
over F. In other words, it is a unital nonassociative algebra A over F with a nondegenerate
Degeneracy (mathematics)
In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
N (called the norm form) such that
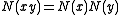
for all x and y in A.
The most well-known example of an octonion algebra are the classical octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s, which are an octonion algebra over R, the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. The split-octonion
Split-octonion
In mathematics, the split-octonions are a nonassociative extension of the quaternions . They differ from the octonions in the signature of quadratic form: the split-octonions have a split-signature whereas the octonions have a positive-definite signature .The split-octonions form the unique split...
s also form an octonion algebra over R. Up to R-algebra isomorphism
Algebra homomorphism
A homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
, these are the only octonion algebras over the reals.
A split octonion algebra is one for which the quadratic form N is isotropic
Isotropic quadratic form
In mathematics, a quadratic form over a field F is said to be isotropic if there is a non-zero vector on which it evaluates to zero. Otherwise the quadratic form is anisotropic. More precisely, if q is a quadratic form on a vector space V over F, then a non-zero vector v in V is said to be...
(i.e. there exists a vector x with N(x) = 0). Up to F-algebra isomorphism, there is a unique split octonion algebra over any field F. When F is algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
or a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, these are the only octonion algebras over F.
Octonion algebras are always nonassociative. They are however alternative algebra
Alternative algebra
In abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...
s (a weaker form of associativity). Moreover, the Moufang identities hold in any octonion algebra. It follows that the set of invertible elements in any octonion algebra form a Moufang loop
Moufang loop
In mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...
, as do the subset of unit norm elements.
Classification
It is a theorem of Adolf HurwitzAdolf Hurwitz
Adolf Hurwitz was a German mathematician.-Early life:He was born to a Jewish family in Hildesheim, former Kingdom of Hannover, now Lower Saxony, Germany, and died in Zürich, in Switzerland. Family records indicate that he had siblings and cousins, but their names have yet to be confirmed...
that the F-isomorphism classes of the norm form are in one-to-one correspondence with the isomorphism classes of octonion F-algebras. Moreover, the possible norm forms are exactly the Pfister 3-forms
Pfister form
In mathematics, a Pfister form is a particular kind of quadratic form over a field F , introduced by A. Pfister in 1965. A Pfister form is in 2n variables, for some natural number n , and may be written as a tensor product of quadratic forms as:\langle \langle a_1, a_2, .....
over F.
Since any two octonion F-algebras become isomorphic over the algebraic closure of F, one can apply the ideas of non-abelian Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
. In particular, by using the fact that the automorphism group of the split octonions is the split algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
G2, one sees the correspondence of isomorphism classes of octonion F-algebras with isomorphism classes of G2-torsors over F. These isomorphism classes form the non-abelian Galois cohomology set
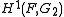 .
.

