Nusselt number
Encyclopedia
In heat transfer
at a boundary (surface) within a fluid
, the Nusselt number is the ratio of convective
to conductive
heat transfer across (normal to) the boundary. Named after Wilhelm Nusselt
, it is a dimensionless number. The conductive component is measured under the same conditions as the heat convection but with a (hypothetically) stagnant (or motionless) fluid.
A Nusselt number close to one, namely convection and conduction of similar magnitude, is characteristic of "slug flow" or laminar flow
. A larger Nusselt number corresponds to more active convection, with turbulent flow typically in the 100–1000 range.
The convection and conduction heat flows are parallel
to each other and to the surface normal
of the boundary surface, and are all perpendicular
to the mean
fluid flow in the simple case.
where:
Selection of the characteristic length should be in the direction of growth (or thickness) of the boundary layer. Some examples of characteristic length are: the outer diameter of a cylinder in (external) cross flow (perpendicular to the cylinder axis), the length of a vertical plate undergoing natural convection
, or the diameter of a sphere. For complex shapes, the length may be defined as the volume of the fluid body divided by the surface area. The thermal conductivity of the fluid is typically (but not always) evaluated at the film temperature
, which for engineering purposes may be calculated as the mean
-average of the bulk fluid temperature and wall surface temperature. For relations defined as a local Nusselt number, one should take the characteristic length to be the distance from the surface boundary to the local point of interest. However, to obtain an average Nusselt number, one must integrate said relation over the entire characteristic length.
Typically, for free convection, the average Nusselt number is expressed as a function of the Rayleigh number
and the Prandtl number, written as: Nu = f(Ra
, Pr). Else, for forced convection, the Nusselt number is generally a function of the Reynolds number and the Prandtl number, or Nu = f(Re, Pr). Empirical correlations for a wide variety of geometries are available that express the Nusselt number in the aforementioned forms.
The mass transfer analog of the Nusselt number is the Sherwood number.
, where q is the heat flux
, k is the thermal conductivity
and T the fluid
temperature
.
Indeed if: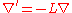
, and 
we arrive at :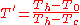
then we define :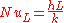
so the equation become :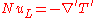
By integrating over the surface of the body:
,
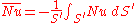where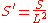
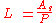
where
is the surface area of the plate and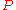 
is its perimeter,
then for the top surface of a hot object in a colder environment or bottom surface of a cold object in a hotter environment
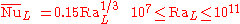
And for the bottom surface of a hot object in a colder environment or top surface of a cold object in a hotter environment
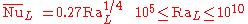
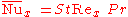
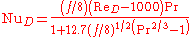
where f is the Darcy friction factor that can either be obtained from the Moody chart
or for smooth tubes from correlation developed by Petukhov:
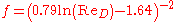
The Gnielinski Correlation is valid for:
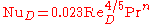
where:
is the inside diameter of the circular duct
is the Prandtl number
for heating of the fluid, and 
for cooling of the fluid.
The Dittus-Boelter equation is valid for
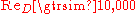
Example The Dittus-Boelter equation is a good approximation where temperature differences between bulk fluid and heat transfer surface are minimal, avoiding equation complexity and iterative solving. Taking water with a bulk fluid average temperature of 20 °C, viscosity 10.07×10¯⁴ Pa·s and a heat transfer surface temperature of 40 °C (viscosity 6.96×10¯⁴, a viscosity correction factor for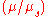
can be obtained as 1.45. This increases to 3.57 with a heat transfer surface temperature of 100 °C (viscosity 2.82×10¯⁴ Pa·s), making a significant difference to the Nusselt number and the heat transfer coefficient.
, as it analyzes the system as a nonlinear boundary value problem
. The Sieder-Tate result can be more accurate as it takes into account the change in viscosity
(
and 
) due to temperature change between the bulk fluid average temperature and the heat transfer surface temperature, respectively. The Sieder-Tate correlation is normally solved by an iterative process, as the viscosity factor will change as the Nusselt number changes.
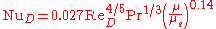
where:
The Sieder-Tate correlation is valid for
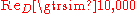
For internal Flow:
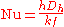
where:
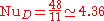
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
at a boundary (surface) within a fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
, the Nusselt number is the ratio of convective
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
to conductive
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
heat transfer across (normal to) the boundary. Named after Wilhelm Nusselt
Wilhelm Nusselt
Ernst Kraft Wilhelm Nußelt was a German engineer. Nusselt studied mechanical engineering at the Munich Technical University , where he got his doctorate in 1907...
, it is a dimensionless number. The conductive component is measured under the same conditions as the heat convection but with a (hypothetically) stagnant (or motionless) fluid.
A Nusselt number close to one, namely convection and conduction of similar magnitude, is characteristic of "slug flow" or laminar flow
Laminar flow
Laminar flow, sometimes known as streamline flow, occurs when a fluid flows in parallel layers, with no disruption between the layers. At low velocities the fluid tends to flow without lateral mixing, and adjacent layers slide past one another like playing cards. There are no cross currents...
. A larger Nusselt number corresponds to more active convection, with turbulent flow typically in the 100–1000 range.
The convection and conduction heat flows are parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to each other and to the surface normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
of the boundary surface, and are all perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
fluid flow in the simple case.
where:
- L = characteristic lengthCharacteristic lengthA characteristic length is an important dimension that defines the scale of a physical system. Often such a length is used as an input to a formula in order to predict some characteristics of the system.Examples:* Reynolds number* Biot number...
- kf = thermal conductivityThermal conductivityIn physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
of the fluid - h = convective heat transfer coefficient
Selection of the characteristic length should be in the direction of growth (or thickness) of the boundary layer. Some examples of characteristic length are: the outer diameter of a cylinder in (external) cross flow (perpendicular to the cylinder axis), the length of a vertical plate undergoing natural convection
Natural convection
Natural convection is a mechanism, or type of heat transport, in which the fluid motion is not generated by any external source but only by density differences in the fluid occurring due to temperature gradients. In natural convection, fluid surrounding a heat source receives heat, becomes less...
, or the diameter of a sphere. For complex shapes, the length may be defined as the volume of the fluid body divided by the surface area. The thermal conductivity of the fluid is typically (but not always) evaluated at the film temperature
Film Temperature
In heat transfer and fluid dynamics, the film temperature is an approximation to the temperature of a fluid inside a convection boundary layer...
, which for engineering purposes may be calculated as the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
-average of the bulk fluid temperature and wall surface temperature. For relations defined as a local Nusselt number, one should take the characteristic length to be the distance from the surface boundary to the local point of interest. However, to obtain an average Nusselt number, one must integrate said relation over the entire characteristic length.
Typically, for free convection, the average Nusselt number is expressed as a function of the Rayleigh number
Rayleigh number
In fluid mechanics, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow...
and the Prandtl number, written as: Nu = f(Ra
Rayleigh number
In fluid mechanics, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow...
, Pr). Else, for forced convection, the Nusselt number is generally a function of the Reynolds number and the Prandtl number, or Nu = f(Re, Pr). Empirical correlations for a wide variety of geometries are available that express the Nusselt number in the aforementioned forms.
The mass transfer analog of the Nusselt number is the Sherwood number.
Derivation
The Nusselt Number may be obtained by a non dimensional analysis of the Fourier's law since it is equal to the dimensionless temperature gradient at the surface:, where q is the heat fluxHeat flux
Heat flux or thermal flux is the rate of heat energy transfer through a given surface. The SI derived unit of heat rate is joule per second, or watt. Heat flux is the heat rate per unit area. In SI units, heat flux is measured in W/m2]. Heat rate is a scalar quantity, while heat flux is a vectorial...
, k is the thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
and T the fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
.
Indeed if:
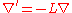, and we arrive at :
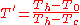
then we define :
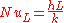
so the equation become :
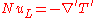
By integrating over the surface of the body:
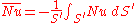,where
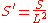
Free convection at a vertical wall
Cited as coming from Churchill and Chu:Free convection from horizontal plates
If the characteristic length is defined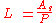where
is the surface area of the plate and 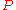is its perimeter,then for the top surface of a hot object in a colder environment or bottom surface of a cold object in a hotter environment
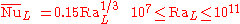
And for the bottom surface of a hot object in a colder environment or top surface of a cold object in a hotter environment
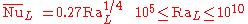
Flat plate in turbulent flow
The local Nusselt number for a turbulant flow is given by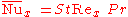Gnielinski correlation
Gnielinski is a correlation for turbulent flow in tubes: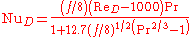where f is the Darcy friction factor that can either be obtained from the Moody chart
Moody chart
The Moody chart or Moody diagram is a graph in non-dimensional form that relates the Darcy friction factor, Reynolds number and relative roughness for fully developed flow in a circular pipe...
or for smooth tubes from correlation developed by Petukhov:
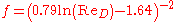
The Gnielinski Correlation is valid for:
Dittus-Boelter equation
The Dittus-Boelter equation (for turbulent flow) is an explicit function for calculating the Nusselt number. It is easy to solve but is less accurate when there is a large temperature difference across the fluid. It is tailored to smooth tubes, so use for rough tubes (most commercial applications) is cautioned. The Dittus-Boelter equation is: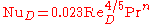where:
is the inside diameter of the circular duct is the Prandtl number for heating of the fluid, and for cooling of the fluid.The Dittus-Boelter equation is valid for
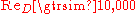
Example The Dittus-Boelter equation is a good approximation where temperature differences between bulk fluid and heat transfer surface are minimal, avoiding equation complexity and iterative solving. Taking water with a bulk fluid average temperature of 20 °C, viscosity 10.07×10¯⁴ Pa·s and a heat transfer surface temperature of 40 °C (viscosity 6.96×10¯⁴, a viscosity correction factor for
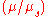can be obtained as 1.45. This increases to 3.57 with a heat transfer surface temperature of 100 °C (viscosity 2.82×10¯⁴ Pa·s), making a significant difference to the Nusselt number and the heat transfer coefficient.Sieder-Tate correlation
The Sieder-Tate correlation for turbulent flow is an implicit functionImplicit function
The implicit function theorem provides a link between implicit and explicit functions. It states that if the equation R = 0 satisfies some mild conditions on its partial derivatives, then one can in principle solve this equation for y, at least over some small interval...
, as it analyzes the system as a nonlinear boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
. The Sieder-Tate result can be more accurate as it takes into account the change in viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
(
and ) due to temperature change between the bulk fluid average temperature and the heat transfer surface temperature, respectively. The Sieder-Tate correlation is normally solved by an iterative process, as the viscosity factor will change as the Nusselt number changes.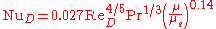where:
-
is the fluid viscosity at the bulk fluid temperature -
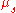is the fluid viscosity at the heat-transfer boundary surface temperature
The Sieder-Tate correlation is valid for
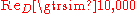
Forced convection in fully developed laminar pipe flow
For fully developed internal laminar flow, the Nusselt numbers are constant-valued. The values depend on the hydraulic diameter.For internal Flow:
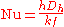
where:
- Dh = Hydraulic diameter
- kf = thermal conductivityThermal conductivityIn physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
of the fluid - h = convective heat transfer coefficient
Convection with uniform surface heat flux for circular tubes
From Incropera & DeWitt,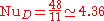Convection with uniform surface temperature for circular tubes
For the case of constant surface temperature,See also
- Sherwood number (mass transfer Nusselt number)
- Churchill-Bernstein EquationChurchill-Bernstein EquationIn convective heat transfer, the Churchill–Bernstein equation is used to estimate the surface averaged Nusselt number for a cylinder in cross flow at various velocities. The need for the equation arises from the inability to solve the Navier–Stokes equations in the turbulent flow regime, even for...
- Reynolds number
- Convective heat transferConvective heat transferConvective heat transfer, often referred to as convection, is the transfer of heat from one place to another by the movement of fluids. The presence of bulk motion of the fluid enhances the heat transfer between the solid surface and the fluid. Convection is usually the dominant form of heat...
- Heat transfer coefficient
- Thermal conductivityThermal conductivityIn physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
External Links
- Simple derivation of the Nusselt number from Newton's law of cooling (Accessed 23 September 2009)