Möbius configuration
Encyclopedia
In geometry
, the Möbius configuration is a certain configuration
in Euclidean space
consisting of two mutually inscribed tetrahedra
: each vertex of one tetrahedron lies on a face plane of the other tetrahedron and vice versa. Thus, for the resulting system of eight points and eight planes, each point lies on four planes (the three planes defining it as a vertex of a tetrahedron and the fourth plane from the other tetrahedron that it lies on), and each plane contains four points (the three tetrahedron vertices of its face, and the vertex from the other tetrahedron that lies on it).
The configuration is named after August Ferdinand Möbius
, who in 1828 proved that, if two tetrahedra have the property that seven of their vertices lie on corresponding face planes of the other tetrahedron, then the eighth vertex also lies on the plane of its corresponding face, forming a configuration of this type. This theorem is true more generally in a three-dimensional projective space if and only if Pappus's theorem
holds for that space (Reidemeister
, Schönhardt
), and it is true for a three-dimensional space modeled on a division ring
if and only if the ring satisfies the commutative law
and is therefore a field
(Al-Dhahir). By projective duality, Möbius' result is equivalent to the statement that, if seven of the eight face planes of two tetrahedra contain the corresponding vertices of the other tetrahedron, then the eighth face plane also contains the same vertex.
describes a simple construction for the configuration. Beginning with an arbitrary point p in Euclidean space, let A, B, C, and D be four planes through p, no three of which share a common intersection line, and place the six points q, r, s, t, u, and v on the six lines formed by pairwise intersection of these planes in such a way that no four of these points are coplanar. For each of the planes A, B, C, and D, four of the seven points p, q, r, s, t, u, and v lie on that plane and three are disjointed from it; form planes A’, B’, C’, and D’ through the triples of points disjoint from A, B, C, and D respectively. Then, by the dual form of Möbius' theorem, these four new planes meet in a single point w. The eight points p, q, r, s, t, u, v, and w and the eight planes A, B, C, D, A’, B’, C’, and D’ form an instance of Möbius' configuration.
Hilbert and Cohn-Vossen (1952) state (without references) that there are five configurations having eight points and eight planes with four points on every plane and four planes through every point that are realisable in three-dimensional
Euclidean space: such configurations have the short-hand notation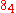
.
They must have obtained their information from the article by .
This actually states, depending upon results by P. Muth (1892), G. Bauer (1897), and V. Martinetti (1897), that there are five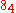
configurations with the property that
at most two planes have two points in common, and dually at most two points are common to two planes. (This condition means that every three points may be non-collinear and dually three planes may not have a line in common.)
However, there are ten other
configurations that do not have this condition, and all fifteen configurations are realizable in real three-dimensional space. The configurations of interest are those with two tetrahedra, each inscribing and circumscribing the other, and these are precisely those that satisfy the above property. Thus, there are five configurations with tetrahedra, and they correspond to the five conjugacy classes of the symmetric group 
.
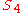One obtains a permutation from the four points of one tetrahedron S = ABCD to itself as follows: each point P of S is on a plane containing three points of the second tetrahedron T. This leaves the other point of T, which is on three points of a plane of S,
leaving another point Q of S, and so the permutation maps P → Q. The five conjugacy classes have representatives e, (12)(34), (12), (123), (1234) and, of these, the Möbius configuration corresponds to the conjugacy class e. It could be denoted Ke.
It is stated by Steinitz that if two of the complementary tetrahedra of Ke are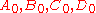
, and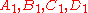 
then the eight planes are given by 
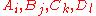with
odd, while the even sums and their complements correspond to all pairs of complementary tetrahedra that in- and circumscribe in the model of Ke.
It is also stated that by Steinitz that the only
that is a geometrical theorem is the Möbius configuration. However that is disputed:
Glynn (2010) shows using a computer search and proofs that there are precisely two
that are actually "theorems": the Möbius configuration
and one other. The latter (which corresponds to the conjugacy class (12)(34) above) is also a theorem for all three-dimensional projective spaces over a field
, but not over a general division ring
. There are other close similarities between the two configurations, including the fact
that both are self-dual under Matroid duality
. In abstract terms, the latter configuration has "points" 0,...,7 and "planes" 0125+i, (i = 0,...,7), where these integers are modulo eight. This configuration, like Möbius, can also be represented
as two tetrahedra, mutually inscribed and circumscribed: in the integer representation the tetrahedra can be 0347 and 1256. However, these two
configurations are non-isomorphic, since Möbius has four pairs of disjoint planes,
while the latter one has no disjoint planes. For a similar reason (and because pairs of planes are degenerate quadratic surfaces), the Möbius configuration is on more quadratic surfaces of three-dimensional space than the latter configuration.
The Levi graph
of the Möbius configuration has 16 vertices, one for each point or plane of the configuration, with an edge for every incident point-plane pair. It is isomorphic to the 16-vertex hypercube graph Q4. A closely related configuration, the Möbius–Kantor configuration
formed by two mutually inscribed quadrilaterals, has the Möbius–Kantor graph
, a subgraph of Q4, as its Levi graph.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Möbius configuration is a certain configuration
Configuration (geometry)
In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.Although certain specific...
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
consisting of two mutually inscribed tetrahedra
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
: each vertex of one tetrahedron lies on a face plane of the other tetrahedron and vice versa. Thus, for the resulting system of eight points and eight planes, each point lies on four planes (the three planes defining it as a vertex of a tetrahedron and the fourth plane from the other tetrahedron that it lies on), and each plane contains four points (the three tetrahedron vertices of its face, and the vertex from the other tetrahedron that lies on it).
The configuration is named after August Ferdinand Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
, who in 1828 proved that, if two tetrahedra have the property that seven of their vertices lie on corresponding face planes of the other tetrahedron, then the eighth vertex also lies on the plane of its corresponding face, forming a configuration of this type. This theorem is true more generally in a three-dimensional projective space if and only if Pappus's theorem
Pappus's hexagon theorem
In mathematics, Pappus's hexagon theorem states that given one set of collinear points A, B, C, and another set of collinear points a, b, c, then the intersection points X, Y, Z of line pairs Ab and aB, Ac and aC, Bc and bC are collinear...
holds for that space (Reidemeister
Kurt Reidemeister
Kurt Werner Friedrich Reidemeister was a mathematician born in Braunschweig , Germany.He received his doctorate in 1921 with a thesis in algebraic number theory at the University of Hamburg under the supervision of Erich Hecke. In 1923 he was appointed assistant professor at the University of Vienna...
, Schönhardt
Erich Schönhardt
Erich Schönhardt was a German mathematician known for his 1928 discovery of the Schönhardt polyhedron, a non-convex polyhedron that cannot be partitioned into tetrahedra without introducing additional vertices.Schönhardt studied at the University of Stuttgart, and went on to do his graduate...
), and it is true for a three-dimensional space modeled on a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
if and only if the ring satisfies the commutative law
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
and is therefore a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(Al-Dhahir). By projective duality, Möbius' result is equivalent to the statement that, if seven of the eight face planes of two tetrahedra contain the corresponding vertices of the other tetrahedron, then the eighth face plane also contains the same vertex.
describes a simple construction for the configuration. Beginning with an arbitrary point p in Euclidean space, let A, B, C, and D be four planes through p, no three of which share a common intersection line, and place the six points q, r, s, t, u, and v on the six lines formed by pairwise intersection of these planes in such a way that no four of these points are coplanar. For each of the planes A, B, C, and D, four of the seven points p, q, r, s, t, u, and v lie on that plane and three are disjointed from it; form planes A’, B’, C’, and D’ through the triples of points disjoint from A, B, C, and D respectively. Then, by the dual form of Möbius' theorem, these four new planes meet in a single point w. The eight points p, q, r, s, t, u, v, and w and the eight planes A, B, C, D, A’, B’, C’, and D’ form an instance of Möbius' configuration.
Hilbert and Cohn-Vossen (1952) state (without references) that there are five configurations having eight points and eight planes with four points on every plane and four planes through every point that are realisable in three-dimensional
Euclidean space: such configurations have the short-hand notation
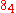.They must have obtained their information from the article by .
This actually states, depending upon results by P. Muth (1892), G. Bauer (1897), and V. Martinetti (1897), that there are five
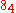configurations with the property thatat most two planes have two points in common, and dually at most two points are common to two planes. (This condition means that every three points may be non-collinear and dually three planes may not have a line in common.)
However, there are ten other
configurations that do not have this condition, and all fifteen configurations are realizable in real three-dimensional space. The configurations of interest are those with two tetrahedra, each inscribing and circumscribing the other, and these are precisely those that satisfy the above property. 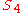Thus, there are five configurations with tetrahedra, and they correspond to the five conjugacy classes of the symmetric group .One obtains a permutation from the four points of one tetrahedron S = ABCD to itself as follows: each point P of S is on a plane containing three points of the second tetrahedron T. This leaves the other point of T, which is on three points of a plane of S,
leaving another point Q of S, and so the permutation maps P → Q. The five conjugacy classes have representatives e, (12)(34), (12), (123), (1234) and, of these, the Möbius configuration corresponds to the conjugacy class e. It could be denoted Ke.
It is stated by Steinitz that if two of the complementary tetrahedra of Ke are
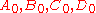, and 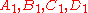then the eight planes are given by 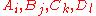with odd, while the even sums and their complements correspond to all pairs of complementary tetrahedra that in- and circumscribe in the model of Ke.It is also stated that by Steinitz that the only
that is a geometrical theorem is the Möbius configuration. However that is disputed:Glynn (2010) shows using a computer search and proofs that there are precisely two
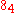that are actually "theorems": the Möbius configurationand one other. The latter (which corresponds to the conjugacy class (12)(34) above) is also a theorem for all three-dimensional projective spaces over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, but not over a general division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
. There are other close similarities between the two configurations, including the fact
that both are self-dual under Matroid duality
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
. In abstract terms, the latter configuration has "points" 0,...,7 and "planes" 0125+i, (i = 0,...,7), where these integers are modulo eight. This configuration, like Möbius, can also be represented
as two tetrahedra, mutually inscribed and circumscribed: in the integer representation the tetrahedra can be 0347 and 1256. However, these two
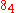configurations are non-isomorphic, since Möbius has four pairs of disjoint planes,while the latter one has no disjoint planes. For a similar reason (and because pairs of planes are degenerate quadratic surfaces), the Möbius configuration is on more quadratic surfaces of three-dimensional space than the latter configuration.
The Levi graph
Levi graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
of the Möbius configuration has 16 vertices, one for each point or plane of the configuration, with an edge for every incident point-plane pair. It is isomorphic to the 16-vertex hypercube graph Q4. A closely related configuration, the Möbius–Kantor configuration
Möbius–Kantor graph
In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor...
formed by two mutually inscribed quadrilaterals, has the Möbius–Kantor graph
Möbius–Kantor graph
In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor...
, a subgraph of Q4, as its Levi graph.