
Matroid
Encyclopedia
In combinatorics
, a branch of mathematics
, a matroid (icon) or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence
in vector space
s.
There are many equivalent ways to define a matroid, and many concepts within matroid theory have a variety of equivalent formulations. Depending on the sophistication of the concept, it may be nontrivial to show that the different formulations are equivalent, a phenomenon sometimes called cryptomorphism
. Significant definitions of matroid include those in terms of independent sets, bases, circuits, closed sets or flats, closure operators, and rank functions.
Matroid theory borrows extensively from the terminology of linear algebra
and graph theory
, largely because it is the abstraction of various notions of central importance in these fields.
s and topologies
.
s of E (called the independent sets) with the following properties:
The first two properties are simple, and define a combinatorial structure known as an independence system
, but the motivation behind the third property is not obvious. The examples in the example section below will make its motivation clearer.
A subset of the ground set E that is not independent is called dependent. A maximal independent set—that is, an independent set which becomes dependent on adding any element of E—is called a basis for the matroid. It is a basic result of matroid theory, directly analogous to a similar theorem of linear algebra
, that any two bases of a matroid M have the same number of elements. This number is called the rank of M.
A circuit in a matroid M is a minimal dependent subset of E—that is, a dependent set whose proper subsets are all independent. In spite of the similarity to the definition of basis this notion has no analogue in classical linear algebra. The terminology comes from graph theory; see below.
The dependent sets, the bases, or the circuits of a matroid characterize the matroid completely. Furthermore, the collection of dependent sets, or of bases, or of circuits each has simple properties that may be taken as axioms for a matroid. For instance, one may define a matroid M to be a pair (E, B), where E is a finite set as before and B is a collection of subsets of E, called "bases", with the following properties:
The rank function r assigns a non-negative integer to every subset of E and has the following properties:
These three properties can be used as one of the alternative definitions of a finite matroid: the independent sets are then defined as those subsets A of E with r(A) = |A|.
The difference |A| − r(A) is called the nullity of the subset A. It is the minimum number of elements that must be removed from A to obtain an independent set. The nullity of E in M is called the nullity of M.
, from P(E) to P(E), where P denotes the power set.
The closure operator cl from P(E) to P(E) has the following property:
In fact this may be taken as another definition of matroid – any closure operator on E with this property determines a matroid on E.
The class L(M) of all flats, partially ordered
by set inclusion, forms a matroid lattice.
Conversely, the set A of atoms of any matroid lattice L form a matroid under the following closure operator: for a set S of atoms whose join in L is x,
Equivalently, the flats of the matroid are the sets
Thus, the lattice of flats of this matroid is naturally isomorphic to L.
. One may define a matroid on E by taking every k-element subset of E to be a basis. This is known as the uniform matroid of rank k. All uniform matroids of rank at least 2 are simple.
The uniform matroid of rank 2 on n points is called the n-point line.
A matroid is uniform if and only if it has no circuits of size less than the one plus the rank of the matroid.
A matroid that is equivalent to a vector matroid, although it may be presented differently, is called representable. If M is equivalent to a vector matroid over a field
F, then we say M is representable over F ; in particular, M is real-representable if it is representable over the real numbers. For instance, although a graphic matroid (see below) is presented in terms of a graph, it is also representable by vectors over any field. A basic problem in matroid theory is to determine whether a given matroid M is representable over a given field F. Whitney
found one solution to this problem when F is a field with two elements (see "Binary matroids", below), but the general situation is famously complicated. The main results so far are characterizations of binary matroids due to Tutte (1950s), of ternary matroids (representable over the 3-element field) due to Reid and Bixby, and separately to Seymour (1970s), and of quaternary matroids (representable over the 4-element field) due to Geelen, Gerards, and Kapoor (2000). This is very much an open area.
.
Every finite graph (or multigraph
) G gives rise to a matroid as follows: take as E the set of all edges in G and consider a set of edges independent if and only if it does not contain a simple cycle. Such an edge set is called a forest in graph theory. This is called the cycle matroid or graphic matroid of G ; it is usually written M(G). The graphic matroid of G can also be defined as the column matroid of any oriented incidence matrix
of G.
Any matroid that is equivalent to the cycle matroid of a (multi)graph, even if it is not presented in terms of graphs, is called a graphic matroid. The matroids that are graphic have been characterized by Tutte
.
Other matroids on graphs were discovered subsequently.
s, and biased graph
s. A graph G with a distinguished linear class B of cycles, known as a "biased graph" (G,B), has two matroids, known as the frame matroid and the lift matroid of the biased graph. If every cycle belongs to the distinguished class, these matroids coincide with the cycle matroid of G. If no cycle is distinguished, the frame matroid is the bicircular matroid of G.
A signed graph, whose edges are labeled by signs, and a gain graph, which is a graph whose edges are labeled orientably from a group, each give rise to a biased graph and therefore have frame and lift matroids.
of A is a subset S of E such that there is a one-to-one function f from S to A by which x belongs to f (x) for each x in S. (A may have repeated members, which are treated as separate subsets of E.) The set of transversals forms the class of independent sets of a matroid, called the transversal matroid of (E, A). These matroids are a special simple case of the Gammoid structures defined above. Simply define a bipartite graph
with A on the left, E on the right, and join X in A to x in E if x is an element of X. The distinguished sets in the gammoid are A and E respectively.
.
An extension of a field gives rise to a matroid. Suppose F and K are fields with K containing F. Let E be any finite subset of K. Define a subset S of E to be independent if the extension field F[S] has transcendence degree
equal to |S|.
A matroid that is equivalent to a matroid of this kind is called an algebraic matroid. The problem of characterizing algebraic matroids is extremely difficult; little is known about it.
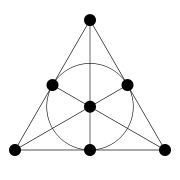 Matroids with a small number of elements are often portrayed with a diagram. The dots are the elements of the underlying set, and a curve has been drawn through every 3-element circuit. The diagram shows a rank 3 matroid called the Fano matroid, an example that appeared in the original 1935 paper of Whitney
Matroids with a small number of elements are often portrayed with a diagram. The dots are the elements of the underlying set, and a curve has been drawn through every 3-element circuit. The diagram shows a rank 3 matroid called the Fano matroid, an example that appeared in the original 1935 paper of Whitney
.
The name arises from the fact that the Fano matroid is the projective plane
of order 2, known as the Fano plane
, whose coordinate field is the 2-element field. This means the Fano matroid is the vector matroid associated to the seven nonzero vectors in a three-dimensional vector space over a field with two elements
.
It is known from projective geometry
that the Fano matroid is not representable by any set of vectors in a real or complex vector space (or in any vector space over a field whose characteristic
differs from 2).
A less famous example is the anti-Fano matroid, defined in the same way as the Fano matroid with the exception that the circle in the above diagram is missing. The anti-Fano matroid is representable over a field if and only if its characteristic differs from 2.
The direct sum of a Fano matroid and an anti-Fano matroid is the simplest example for a matroid which is not representable over any field.
 On the other hand, consider this non-example: let E be a set of pairs (v,c) where v ranges over the vertices of a graph and c ranges over the set {red, blue, yellow}. Let the independent sets be the sets of pairs that associate only one color with each vertex and do not associate the same color with two adjacent vertices; that is, they represent valid graph coloring
On the other hand, consider this non-example: let E be a set of pairs (v,c) where v ranges over the vertices of a graph and c ranges over the set {red, blue, yellow}. Let the independent sets be the sets of pairs that associate only one color with each vertex and do not associate the same color with two adjacent vertices; that is, they represent valid graph coloring
s. The empty set is a valid three-coloring, and any subset of a valid three-coloring is a valid three-coloring, but the exchange property does not hold, because it's possible to have two maximal three-colored subgraphs of different sizes, as shown to the right. It's no surprise that this is not a matroid, since if it were, it would give us a greedy algorithm for the NP-complete 3-coloring problem, showing P = NP.
There are some standard ways to make new matroids out of old ones.
For this he used his difficult homotopy theorem. Simpler proofs have since been found.
Seymour's decomposition theorem states that all regular matroids can be built up in a simple way as the clique-sum
of graphic matroids, their duals, and one special matroid. This theorem has major consequences for linear programming
involving totally unimodular matrices.
and Tutte found famous characterizations. Addition of sets is symmetric difference
. The following properties of a matroid M are equivalent:
The monograph of Recski compiled 8 equivalent definitions of binary matroids.
It is easy to show that the matroids representable over a fixed field can be characterized by a list of forbidden minors. A famous outstanding problem (Rota's conjecture) is to prove that this list is finite for finite fields. This has been solved only for the fields of up to four elements (and the exact lists are known for those fields, but one cannot expect exact lists for larger fields). The problem is significant because there are matroid properties that can be characterized by forbidden minors but not by a finite list of them—for example, the property of being representable over the real numbers. (The nonexistence of any finite set of axioms for real-representable matroids is a famous theorem of Vamos (1978).)
The Robertson–Seymour theorem
implies that every matroid property of graphic matroids characterized by a list of forbidden minors can be characterized by a finite list—in other words, if an infinite list L includes the forbidden minors for graphic matroids, then Ex(L) = Ex(L’) for some finite list L’. Strengthening Rota's conjecture, Robertson and Seymour conjectured that a similar theorem holds more generally for the matroids representable over any fixed finite field
. So far, this has been proven for matroids with bounded branchwidth .
The dual can be described equally well in terms of other ways to define a matroid. For instance:
A main result is the matroid version of Kuratowski's theorem: The dual of a graphic matroid M is a graphic matroid if and only if M is the matroid of a planar graph
. In this case, the dual of M is the matroid of the dual graph
of G.
A simpler result is that the dual of a vector matroid representable over a particular field F is also representable over F.
It is known that the dual of a transversal matroid is a strict gammoid and vice versa. See Box 15.2 in the monograph of Recski for the relations among gammoids, strict gammoids, transversal and fundamental transversal matroids
s. Such a weight function w can be extended to subsets S ⊆ E by defining
Suppose E is a finite set, F a nonempty family of subsets of E such that any subset of any element of F also belongs to F, and w: F → R+ a weight function on F. A greedy algorithm
for (E, F, w) is any algorithm
that attempts to construct a maximum weight element of F as follows:
The following two theorems establish a correspondence between matroids and sets (E, F) as defined above for which greedy algorithms do give maximum weight solutions.
The notion of matroid has been generalized to allow for other types of sets on which greedy algorithms give optimal solutions; see greedoid
for more information.
The simplest definition of an infinite matroid is to require finite rank; that is, the rank of E is finite. This theory is similar to that of finite matroids except for the failure of duality due to the fact that the dual of an infinite matroid of finite rank does not have finite rank. Finite-rank matroids include any subsets of finite-dimensional vector spaces and of field extensions
of finite transcendence degree
.
The next simplest infinite generalization is finitary matroids. A matroid is finitary if it has the property that
Equivalently, every dependent set contains a finite dependent set.
Examples are linear dependence of arbitrary subsets of infinite-dimensional vector spaces (but not infinite dependencies as in Hilbert
and Banach space
s), and algebraic dependence in arbitrary subsets of field extensions of possibly infinite transcendence degree. Again, the class of finitary matroid is not self-dual, because the dual of a finitary matroid is not finitary.
Finitary infinite matroids are studied in model theory
, a branch of mathematical logic
with strong ties to algebra
.
In the late 1960s matroid theorists asked for a more general notion that shares the different aspects of finite matroids and generalizes their duality. Many notions of infinite matroids were defined in response to this challenge, but the question remained open. One of the approaches examined by D.A. Higgs became known as B-matroids and was studied by Higgs, Oxley and others in the 1960s and 1970s. According to a recent result by Bruhn, Diestel, Kriesell and Wollan (2010), it solves the problem: Arriving at the same notion independently, they provided four different systems of axioms – in terms of independence, bases, circuits and closure. The duality of B-matroids generalizes dualities that can be observed in infinite graphs.

or equivalently (as long as the empty set is closed in M) as
When M is the cycle matroid M(G) of a graph G, the characteristic polynomial is a slight transformation of the chromatic polynomial
, which is given by χG (λ) = λcpM(G) (λ), where c is the number of connected components of G.
When M is the bond matroid M*(G) of a graph G, the characteristic polynomial equals the flow polynomial of G.
When M is the matroid of an arrangement
A of linear hyperplanes in Rn, the characteristic polynomial of the arrangement is given by pA (λ) = λn−r(M)pM(A) (λ).
of a matroid, TM (x,y), generalizes the characteristic polynomial to two variables. This gives it more combinatorial interpretations, and also gives it the duality property
which implies a number of dualities between properties of M and properties of M *. One definition of the Tutte polynomial is
This expresses the Tutte polynomial as an evaluation of the corank-nullity or rank generating polynomial,
Another definition is in terms of internal and external activities and a sum over bases. This, which sums over fewer subsets but has more complicated terms, was Tutte's original definition.
The Tutte polynomial
TG of a graph is the Tutte polynomial TM(G) of its cycle matroid.
"Oid" is an open source, interactive, extensible software system for experimenting with matroids.
"Macek" is a specialized software system with tools and routines for reasonably efficient combinatorial computations with representable matroids.
, whose work was forgotten for many years .
In his seminal paper, Whitney provided two axioms for independence, and defined any structure adhering to these axioms to be "matroids".
(Although it was perhaps implied, he did not include an axiom requiring at least one subset to be independent.)
His key observation was that these axioms provide an abstraction of "independence" that is common to both graphs and matrices.
Because of this, many of the terms used in matroid theory resemble the terms for their analogous concepts in linear algebra
or graph theory
.
Almost immediately after Whitney first wrote about matroids, an important article was written by on the relation of matroids to projective geometry. A year later, noted similarities between algebraic and linear dependence in his classic textbook on Modern Algebra.
In the 1940s Richard Rado
developed further theory under the name "independence systems" with an eye towards transversal theory, where his name for the subject is still sometimes used.
In the 1950s W. T. Tutte
became the foremost figure in matroid theory, a position he retained for many years. His contributions were plentiful, including the characterization of binary, regular, and graphic matroids by excluded minors; the regular-matroid representability theorem; the theory of chain groups and their matroids; and the tools he used to prove many of his results, the "Path Theorem" and "Homotopy Theorem" (see, e.g.), which are so complex that later theorists have gone to great trouble to eliminate the necessity of using them in proofs. (A fine example is A. M. H. Gerards' short proof (1989) of Tutte's characterization of regular matroids.)
and generalized to matroids Tutte's "dichromate", a graphic polynomial now known as the Tutte polynomial
(named by Crapo). Their work has recently been followed by a flood of papers—though not as many as on the Tutte polynomial of a graph.
In 1976 Dominic Welsh published the first comprehensive book on matroid theory.
Paul Seymour's decomposition theorem for regular matroids (1980) was the most significant and influential work of the late 1970s and the 1980s.
Another fundamental contribution, by , showed why projective geometries and Dowling geometries play such an important role in matroid theory.
By this time there were many other important contributors, but one should not omit to mention Geoff Whittle's extension to ternary matroids of Tutte's characterization of binary matroids that are representable over the rationals , perhaps the biggest single contribution of the 1990s. In the current decade the Matroid Minors Project of Geelen
, Gerards, Whittle, and others, which attempts to duplicate for matroids that are representable over a finite field the success of the Robertson–Seymour Graph Minors Project (see Robertson–Seymour theorem
), has produced substantial advances in the structure theory of matroids. Many others have also contributed to that part of matroid theory, which is presently flourishing.
Other major contributors include:
There is an on-line list of current researchers.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a matroid (icon) or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
in vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s.
There are many equivalent ways to define a matroid, and many concepts within matroid theory have a variety of equivalent formulations. Depending on the sophistication of the concept, it may be nontrivial to show that the different formulations are equivalent, a phenomenon sometimes called cryptomorphism
Cryptomorphism
In mathematics, two objects, especially systems of axioms or semantics for them, are called cryptomorphic if they are equivalent but not obviously equivalent...
. Significant definitions of matroid include those in terms of independent sets, bases, circuits, closed sets or flats, closure operators, and rank functions.
Matroid theory borrows extensively from the terminology of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, largely because it is the abstraction of various notions of central importance in these fields.
Formal definitions of finite matroids
There are dozens of equivalent ways to define a (finite) matroid. Here are some of the most important. There is no one preferred or customary definition; in that respect, matroids differ from many other mathematical structures, such as groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s and topologies
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Independent sets, bases, and circuits
One of the most valuable definitions is that given in terms of independence. In this definition a finite matroid M is a pair (E, I), where E is a finite set (called the ground set) and I is a collection of subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of E (called the independent sets) with the following properties:
- The empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is independent, i.e., ∅ ∈ I. (Alternatively, at least one subset of E is independent, i.e., I ≠ ∅.) - Every subset of an independent set is independent, i.e., for each A' ⊆ A ⊆ E, A ∈ I → A' ∈ I. This is sometimes called the hereditary property.
- If A and B are two independent sets of I and A has more elements than B, then there exists an element in A which is not in B that when added to B still gives an independent set. This is sometimes called the augmentation property or the independent set exchange property.
The first two properties are simple, and define a combinatorial structure known as an independence system
Independence system
In combinatorial mathematics, an independence system S is a pair , where E is a finite set and I is a collection of subsets of E with the following properties:...
, but the motivation behind the third property is not obvious. The examples in the example section below will make its motivation clearer.
A subset of the ground set E that is not independent is called dependent. A maximal independent set—that is, an independent set which becomes dependent on adding any element of E—is called a basis for the matroid. It is a basic result of matroid theory, directly analogous to a similar theorem of linear algebra
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, that any two bases of a matroid M have the same number of elements. This number is called the rank of M.
A circuit in a matroid M is a minimal dependent subset of E—that is, a dependent set whose proper subsets are all independent. In spite of the similarity to the definition of basis this notion has no analogue in classical linear algebra. The terminology comes from graph theory; see below.
The dependent sets, the bases, or the circuits of a matroid characterize the matroid completely. Furthermore, the collection of dependent sets, or of bases, or of circuits each has simple properties that may be taken as axioms for a matroid. For instance, one may define a matroid M to be a pair (E, B), where E is a finite set as before and B is a collection of subsets of E, called "bases", with the following properties:
- B is nonempty.
- No member of B is a proper subset of another.
- If A and B are distinct members of B and a is an element of A not belonging to B, then there exists an element b belonging to B-A such that A − a + b is a basis. (This property is called the basis exchange property.)
Rank functions
If M is a matroid on E, and A is a subset of E, then a matroid on A can be defined by considering a subset of A independent if and only if it is independent in M. This allows us to talk about submatroids and about the rank of any subset of E.The rank function r assigns a non-negative integer to every subset of E and has the following properties:
- r(A) ≤ |A| for all subsets A of E. (Cardinality bound)
- If A and B are subsets of E with A ⊆ B, then r(A) ≤ r(B). (Increase)
- For any two subsets A and B of E, we have r(A ∪ B) + r(A ∩ B) ≤ r(A) + r(B). (Submodularity)
These three properties can be used as one of the alternative definitions of a finite matroid: the independent sets are then defined as those subsets A of E with r(A) = |A|.
The difference |A| − r(A) is called the nullity of the subset A. It is the minimum number of elements that must be removed from A to obtain an independent set. The nullity of E in M is called the nullity of M.
Closure operators
Let M be a matroid on a finite set E, defined as above. The closure cl(A) of a subset A of E is the subset of E containing A and every element x in E\A, such that there is a circuit C containing x and contained in the union of A and {x}. This defines the closure operatorClosure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
, from P(E) to P(E), where P denotes the power set.
The closure operator cl from P(E) to P(E) has the following property:
- For all elements a, b of E and all subsets Y of E, if a is in cl(Y ∪ b) \ cl(Y), then b is in cl(Y ∪ a) \ cl(Y). This is sometimes called the Mac Lane–Steinitz exchange property.
In fact this may be taken as another definition of matroid – any closure operator on E with this property determines a matroid on E.
Closed sets (flats)
A set whose closure equals itself is said to be closed, or a flat of the matroid. The closed sets of a matroid are characterized by a covering partition property:- The whole point set E is closed.
- If S and T are flats, then S ∩ T is a flat.
- If S is a flat, then the flats T that cover S, i.e., T properly contains S but there is no flat U between S and T, partition the elements of E − S.
The class L(M) of all flats, partially ordered
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
by set inclusion, forms a matroid lattice.
Conversely, the set A of atoms of any matroid lattice L form a matroid under the following closure operator: for a set S of atoms whose join in L is x,
- cl(S) = {a ∈ A | a ≤ x}.
Equivalently, the flats of the matroid are the sets
- {a∈A | a ≤ x} for x ∈ L.
Thus, the lattice of flats of this matroid is naturally isomorphic to L.
Simple matroids
A matroid is called simple if it has no circuits consisting of 1 or 2 elements. That is, it has no loops and no parallel elements.Uniform matroids
Let E be a finite set and k a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. One may define a matroid on E by taking every k-element subset of E to be a basis. This is known as the uniform matroid of rank k. All uniform matroids of rank at least 2 are simple.
The uniform matroid of rank 2 on n points is called the n-point line.
A matroid is uniform if and only if it has no circuits of size less than the one plus the rank of the matroid.
Discrete matroids
A matroid is called discrete if every element is a loop or a coloop. Equivalently, every proper, non-empty subset of the ground set E is a separator (loop, coloop, and separator are defined in Additional Terminology below).Matroids from linear algebra
Matroid theory developed mainly out of a deep examination of the properties of independence and dimension in vector spaces. Matroids from vector spaces are still the main examples. There are two ways to present them.- If E is any finite subset of a vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V, then we can define a matroid M on E by taking the independent sets of M to be the linearly independentLinear independenceIn linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
subsets of E. We say the set E represents M. Matroids of this kind are called vector matroids. - A matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A with entries in a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
gives rise to a matroid M on its set of columns. The dependent sets of columns in the matroid are those that are linearly dependent as vectors. This matroid is called the column matroid of A, and A is said to represent M. Column matroids are just vector matroids under another name, but there are often reasons to favor the matrix representation. (There is one technical difference: a column matroid can have distinct elements that are the same vector, but a vector matroid as defined above cannot. Usually this difference is insignificant and can be ignored, but by letting E be a multisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of vectors one brings the two definitions into complete agreement.)
A matroid that is equivalent to a vector matroid, although it may be presented differently, is called representable. If M is equivalent to a vector matroid over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F, then we say M is representable over F ; in particular, M is real-representable if it is representable over the real numbers. For instance, although a graphic matroid (see below) is presented in terms of a graph, it is also representable by vectors over any field. A basic problem in matroid theory is to determine whether a given matroid M is representable over a given field F. Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
found one solution to this problem when F is a field with two elements (see "Binary matroids", below), but the general situation is famously complicated. The main results so far are characterizations of binary matroids due to Tutte (1950s), of ternary matroids (representable over the 3-element field) due to Reid and Bixby, and separately to Seymour (1970s), and of quaternary matroids (representable over the 4-element field) due to Geelen, Gerards, and Kapoor (2000). This is very much an open area.
Matroids from graph theory
A second original source for the theory of matroids is graph theoryGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
.
Every finite graph (or multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
) G gives rise to a matroid as follows: take as E the set of all edges in G and consider a set of edges independent if and only if it does not contain a simple cycle. Such an edge set is called a forest in graph theory. This is called the cycle matroid or graphic matroid of G ; it is usually written M(G). The graphic matroid of G can also be defined as the column matroid of any oriented incidence matrix
Incidence matrix
In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
of G.
Any matroid that is equivalent to the cycle matroid of a (multi)graph, even if it is not presented in terms of graphs, is called a graphic matroid. The matroids that are graphic have been characterized by Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
.
Other matroids on graphs were discovered subsequently.
- The bicircular matroidBicircular matroidIn the mathematical subject of matroid theory, the bicircular matroid of a graph G is the matroid B whose points are the edges of G and whose independent sets are the edge sets of pseudoforests of G, that is, the edge sets in which each connected component contains at most one cycle...
of a graph is defined by calling a set of edges independent if every connected subset contains at most one cycle. - In any directed or undirected graph G let E and F be two distinguished sets of vertices. In the set E, define a subset U to be independent if there are |U| vertex-disjoint paths from F onto U. This defines a matroid on E called a gammoid.
Matroids from biased graphs
Graphic matroids have been generalized to matroids from signed graphs, gain graphGain graph
A gain graph is a graph whose edges are labelled "invertibly", or "orientably", by elements of a group G. This means that, if an edge e in one direction has label g , then in the other direction it has label g −1...
s, and biased graph
Biased graph
In mathematics, a biased graph is a graph with a list of distinguished circles , such that if two circles in the list are contained in a theta graph, then so is the third circle of the theta graph...
s. A graph G with a distinguished linear class B of cycles, known as a "biased graph" (G,B), has two matroids, known as the frame matroid and the lift matroid of the biased graph. If every cycle belongs to the distinguished class, these matroids coincide with the cycle matroid of G. If no cycle is distinguished, the frame matroid is the bicircular matroid of G.
A signed graph, whose edges are labeled by signs, and a gain graph, which is a graph whose edges are labeled orientably from a group, each give rise to a biased graph and therefore have frame and lift matroids.
Frame matroids
A matroid M is called a frame matroid if it, or a matroid that contains it, has a basis such that all the points of M are contained in the lines that join pairs of basis elements.Transversal matroids
Given a set of "points", E, and a class A of subsets of E, a transversalTransversal
In geometry , when two coplanar lines exist such that a third coplanar line passes thru both lines. This third line is named the Transversal....
of A is a subset S of E such that there is a one-to-one function f from S to A by which x belongs to f (x) for each x in S. (A may have repeated members, which are treated as separate subsets of E.) The set of transversals forms the class of independent sets of a matroid, called the transversal matroid of (E, A). These matroids are a special simple case of the Gammoid structures defined above. Simply define a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
with A on the left, E on the right, and join X in A to x in E if x is an element of X. The distinguished sets in the gammoid are A and E respectively.
Matroids from field extensions
A third original source of matroid theory is field theoryField theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
.
An extension of a field gives rise to a matroid. Suppose F and K are fields with K containing F. Let E be any finite subset of K. Define a subset S of E to be independent if the extension field F[S] has transcendence degree
Transcendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
equal to |S|.
A matroid that is equivalent to a matroid of this kind is called an algebraic matroid. The problem of characterizing algebraic matroids is extremely difficult; little is known about it.
The Fano matroid

Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
.
The name arises from the fact that the Fano matroid is the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
of order 2, known as the Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
, whose coordinate field is the 2-element field. This means the Fano matroid is the vector matroid associated to the seven nonzero vectors in a three-dimensional vector space over a field with two elements
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
.
It is known from projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
that the Fano matroid is not representable by any set of vectors in a real or complex vector space (or in any vector space over a field whose characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
differs from 2).
A less famous example is the anti-Fano matroid, defined in the same way as the Fano matroid with the exception that the circle in the above diagram is missing. The anti-Fano matroid is representable over a field if and only if its characteristic differs from 2.
The direct sum of a Fano matroid and an anti-Fano matroid is the simplest example for a matroid which is not representable over any field.
Non-examples

Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
s. The empty set is a valid three-coloring, and any subset of a valid three-coloring is a valid three-coloring, but the exchange property does not hold, because it's possible to have two maximal three-colored subgraphs of different sizes, as shown to the right. It's no surprise that this is not a matroid, since if it were, it would give us a greedy algorithm for the NP-complete 3-coloring problem, showing P = NP.
Basic constructions
Let M be a matroid with an underlying set of elements E, and let N be another matroid on underlying set F.There are some standard ways to make new matroids out of old ones.
- Restriction. If S is a subset of E, the restriction of M to S, written M |S, is the matroid on underlying set S whose independent sets are the independent sets of M that are contained in S. Its circuits are the circuits of M that are contained in S and its rank function is that of M restricted to subsets of S. In linear algebra, this corresponds to restricting to the subspace generated by the vectors in S.
- Contraction. If T is a subset of E, the contraction of M by T, written M/T, is the matroid on the underlying set E − T whose rank function is
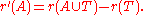 In linear algebra, this corresponds to looking at the quotient space by the linear space generated by the vectors in T, together with the images of the vectors in E - T.
In linear algebra, this corresponds to looking at the quotient space by the linear space generated by the vectors in T, together with the images of the vectors in E - T. - Minors. A matroid N that is obtained from M by a sequence of restriction and contraction operations is called a minor of M. We say M contains N as a minor.
- Direct sum. The direct sum of M and N is the matroid whose underlying set is the disjoint unionDisjoint unionIn mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of E and F, and whose independent sets are the disjoint unions of an independent set of M with an independent set of N.
- Theorem. A matroid is the direct sum
 of its restrictions to its irreducible separators
of its restrictions to its irreducible separators  .
.
- Matroid union. The union of M and N is the matroid whose underlying set is the union (not the disjoint union) of E and F, and whose independent sets are those subsets which are the union of an independent set in M and one in N. Usually the term "union" is applied when E = F, but that assumption is not essential. If E and F are disjoint, the union is the direct sum.
Additional terminology
Let M be a matroid with an underlying set of elements E.- A subset of E spans M if its closure is E. A set is said to span a closed set K if its closure is K.
- A maximal closed proper subset of E is called a coatom or copoint or hyperplane of M. An equivalent definition: A coatom is a subset of E that does not span M, but such that adding any other element to it does make a spanning set.
- An element that forms a single-element circuit of M is called a loop. Equivalently, an element is a loop if it belongs to no basis.
- An element that belongs to no circuit is called a coloop. Equivalently, an element is a coloop if it belongs to every basis.
- If a two-element set {f, g} is a circuit of M, then f and g are parallel in M.
- A simple matroid obtained from M by deleting all loops and deleting one element from each 2-element circuit until no 2-element circuits remain is called a simplification of M.
- A separator of M is a subset S of E such that
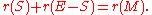 A proper separator is a separator that is neither E nor the empty set. An irreducible separator is a separator that contains no other non-empty separator. The irreducible separators partition the ground set E.
A proper separator is a separator that is neither E nor the empty set. An irreducible separator is a separator that contains no other non-empty separator. The irreducible separators partition the ground set E. - A matroid which cannot be written as the direct sum of two nonempty matroids, or equivalently which has no proper separators, is called connected or irreducible.
- A maximal irreducible submatroid of M is called a component of M. A component is the restriction of M to an irreducible separator, and contrariwise, the restriction of M to an irreducible separator is a component.
Regular matroids
A matroid is regular if it can be represented by a totally unimodular matrix (a matrix whose square submatrices all have determinants equal to 0, 1, or −1). Tutte proved that the following three properties of a matroid are logically equivalent:- M is regular.
- M is representable over every field.
- M has no minor that is a four-point line or a Fano plane or its dual.
For this he used his difficult homotopy theorem. Simpler proofs have since been found.
Seymour's decomposition theorem states that all regular matroids can be built up in a simple way as the clique-sum
Clique-sum
In graph theory, a branch of mathematics, a clique-sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology...
of graphic matroids, their duals, and one special matroid. This theorem has major consequences for linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
involving totally unimodular matrices.
Binary matroids
A matroid that is representable over the two-element field is called a binary matroid. Binary matroids include graphic and regular matroids. They have many of the nice properties of those types of matroid. WhitneyHassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
and Tutte found famous characterizations. Addition of sets is symmetric difference
Symmetric difference
In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
. The following properties of a matroid M are equivalent:
- M is binary.
- In M, every sum of circuits is a union of disjoint circuits (Whitney).
- M has no minor that is a four-point line (Tutte).
The monograph of Recski compiled 8 equivalent definitions of binary matroids.
Forbidden minors
Suppose L is a list of matroids. The class Ex(L) of all matroids that do not contain as a minor any member of the list is said to be characterized by forbidden minors (or excluded minors). Some of the great theorems of matroid theory characterize natural classes of matroids by forbidden minors. Three examples due to Tutte are:- Binary matroids (see above).
- Regular matroids (see above).
- Graphic matroids: the matroids that have no minor that is the four-point line (which is self-dual), the Fano plane or its dual, the dual of the cycle matroid M(K5), or the dual of the cycle matroid M(K3,3).
It is easy to show that the matroids representable over a fixed field can be characterized by a list of forbidden minors. A famous outstanding problem (Rota's conjecture) is to prove that this list is finite for finite fields. This has been solved only for the fields of up to four elements (and the exact lists are known for those fields, but one cannot expect exact lists for larger fields). The problem is significant because there are matroid properties that can be characterized by forbidden minors but not by a finite list of them—for example, the property of being representable over the real numbers. (The nonexistence of any finite set of axioms for real-representable matroids is a famous theorem of Vamos (1978).)
The Robertson–Seymour theorem
Robertson–Seymour theorem
In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering...
implies that every matroid property of graphic matroids characterized by a list of forbidden minors can be characterized by a finite list—in other words, if an infinite list L includes the forbidden minors for graphic matroids, then Ex(L) = Ex(L’) for some finite list L’. Strengthening Rota's conjecture, Robertson and Seymour conjectured that a similar theorem holds more generally for the matroids representable over any fixed finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
. So far, this has been proven for matroids with bounded branchwidth .
Matroid duality
If M is a finite matroid, we can define the dual matroid M* by taking the same underlying set and calling a set a basis in M* if and only if its complement is a basis in M. It is not difficult to verify that M* is a matroid and that the dual of M* is M.The dual can be described equally well in terms of other ways to define a matroid. For instance:
- A set is independent in M* if and only if its complement spans M.
- A set is a circuit of M* if and only if its complement is a coatom in M.
- The rank function of the dual is r*(S) = |S|- r(E) + r(E\S).
A main result is the matroid version of Kuratowski's theorem: The dual of a graphic matroid M is a graphic matroid if and only if M is the matroid of a planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
. In this case, the dual of M is the matroid of the dual graph
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
of G.
A simpler result is that the dual of a vector matroid representable over a particular field F is also representable over F.
It is known that the dual of a transversal matroid is a strict gammoid and vice versa. See Box 15.2 in the monograph of Recski for the relations among gammoids, strict gammoids, transversal and fundamental transversal matroids
Greedy algorithms
A weight function on a finite set E is a function w: E → R+ from E to the nonnegative real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. Such a weight function w can be extended to subsets S ⊆ E by defining
- w(S) = ∑s ∈ S w(s).
Suppose E is a finite set, F a nonempty family of subsets of E such that any subset of any element of F also belongs to F, and w: F → R+ a weight function on F. A greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
for (E, F, w) is any algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that attempts to construct a maximum weight element of F as follows:
- 1. Let F0 = ∅.
- 2. For i ≥ 0:
- 3. Let Zi = { zi ∈ E-Fi | Fi ∪ {zi} ∈ F }.
- 4. If Zi = ∅, terminate and return Fi .
- 5. Otherwise, choose an element y ∈ Zi such that w(y) = max{w(zi), zi ∈ Zi}, let Fi+1 = Fi ∪ {y} and continue.
The following two theorems establish a correspondence between matroids and sets (E, F) as defined above for which greedy algorithms do give maximum weight solutions.
- Theorem 1: If E in (E, F, w) is the underlying set of a matroid M and F is the set of independent sets in M, then any greedy algorithm for (E, F, w) constructs a maximum weight element of F.
- Theorem 2: If every greedy algorithm for the pair (E, F) constructs a maximum weight element of F for every choice of weight function w: F → R+ then F is the set of independent sets of a matroid M with underlying set E.
The notion of matroid has been generalized to allow for other types of sets on which greedy algorithms give optimal solutions; see greedoid
Greedoid
In combinatorics, a greedoid is a type of set system. It arises from the notion of the matroid, which was originally introduced by Whitney in 1935 to study planar graphs and was later used by Edmonds to characterize a class of optimization problems that can be solved by greedy algorithms...
for more information.
Infinite matroids
The theory of infinite matroids is much more complicated than that of finite matroids and forms a subject of its own. For a long time, one of the difficulties has been that there were many reasonable and useful definitions, none of which appeared to capture all the important aspects of finite matroid theory. For instance, it seemed to be hard to have bases, circuits, and duality together in one notion of infinite matroids.The simplest definition of an infinite matroid is to require finite rank; that is, the rank of E is finite. This theory is similar to that of finite matroids except for the failure of duality due to the fact that the dual of an infinite matroid of finite rank does not have finite rank. Finite-rank matroids include any subsets of finite-dimensional vector spaces and of field extensions
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of finite transcendence degree
Transcendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
.
The next simplest infinite generalization is finitary matroids. A matroid is finitary if it has the property that

Equivalently, every dependent set contains a finite dependent set.
Examples are linear dependence of arbitrary subsets of infinite-dimensional vector spaces (but not infinite dependencies as in Hilbert
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s), and algebraic dependence in arbitrary subsets of field extensions of possibly infinite transcendence degree. Again, the class of finitary matroid is not self-dual, because the dual of a finitary matroid is not finitary.
Finitary infinite matroids are studied in model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a branch of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
with strong ties to algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
In the late 1960s matroid theorists asked for a more general notion that shares the different aspects of finite matroids and generalizes their duality. Many notions of infinite matroids were defined in response to this challenge, but the question remained open. One of the approaches examined by D.A. Higgs became known as B-matroids and was studied by Higgs, Oxley and others in the 1960s and 1970s. According to a recent result by Bruhn, Diestel, Kriesell and Wollan (2010), it solves the problem: Arriving at the same notion independently, they provided four different systems of axioms – in terms of independence, bases, circuits and closure. The duality of B-matroids generalizes dualities that can be observed in infinite graphs.
Polynomial invariants
There are two especially significant polynomials associated to a finite matroid M on the ground set E. Each is a matroid invariant, which means that isomorphic matroids have the same polynomial.Characteristic polynomial
The characteristic polynomial of M (which is sometimes called the chromatic polynomial, although it does not count colorings), is defined to be
or equivalently (as long as the empty set is closed in M) as

When M is the cycle matroid M(G) of a graph G, the characteristic polynomial is a slight transformation of the chromatic polynomial
Chromatic polynomial
The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
, which is given by χG (λ) = λcpM(G) (λ), where c is the number of connected components of G.
When M is the bond matroid M*(G) of a graph G, the characteristic polynomial equals the flow polynomial of G.
When M is the matroid of an arrangement
Arrangement of hyperplanes
In geometry and combinatorics, an arrangement of hyperplanes is a finite set A of hyperplanes in a linear, affine, or projective space S....
A of linear hyperplanes in Rn, the characteristic polynomial of the arrangement is given by pA (λ) = λn−r(M)pM(A) (λ).
Tutte polynomial
The Tutte polynomialTutte polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
of a matroid, TM (x,y), generalizes the characteristic polynomial to two variables. This gives it more combinatorial interpretations, and also gives it the duality property

which implies a number of dualities between properties of M and properties of M *. One definition of the Tutte polynomial is

This expresses the Tutte polynomial as an evaluation of the corank-nullity or rank generating polynomial,

Another definition is in terms of internal and external activities and a sum over bases. This, which sums over fewer subsets but has more complicated terms, was Tutte's original definition.
The Tutte polynomial
Tutte polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
TG of a graph is the Tutte polynomial TM(G) of its cycle matroid.
Matroid software
Two systems for calculations with matroids are Kingan's Oid and Hlineny's Macek."Oid" is an open source, interactive, extensible software system for experimenting with matroids.
"Macek" is a specialized software system with tools and routines for reasonably efficient combinatorial computations with representable matroids.
History
Matroid theory was introduced by . It was also independently discovered by Takeo NakasawaTakeo Nakasawa
Takeo Nakasawa was a Japanese mathematician who independently invented matroid theory, though his work was forgotten for many years....
, whose work was forgotten for many years .
In his seminal paper, Whitney provided two axioms for independence, and defined any structure adhering to these axioms to be "matroids".
(Although it was perhaps implied, he did not include an axiom requiring at least one subset to be independent.)
His key observation was that these axioms provide an abstraction of "independence" that is common to both graphs and matrices.
Because of this, many of the terms used in matroid theory resemble the terms for their analogous concepts in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
or graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
.
Almost immediately after Whitney first wrote about matroids, an important article was written by on the relation of matroids to projective geometry. A year later, noted similarities between algebraic and linear dependence in his classic textbook on Modern Algebra.
In the 1940s Richard Rado
Richard Rado
Richard Rado FRS was a Jewish German mathematician. He earned two Ph.D.s: in 1933 from the University of Berlin, and in 1935 from the University of Cambridge. He was interviewed in Berlin by Lord Cherwell for a scholarship given by the chemist Sir Robert Mond which provided financial support to...
developed further theory under the name "independence systems" with an eye towards transversal theory, where his name for the subject is still sometimes used.
In the 1950s W. T. Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
became the foremost figure in matroid theory, a position he retained for many years. His contributions were plentiful, including the characterization of binary, regular, and graphic matroids by excluded minors; the regular-matroid representability theorem; the theory of chain groups and their matroids; and the tools he used to prove many of his results, the "Path Theorem" and "Homotopy Theorem" (see, e.g.), which are so complex that later theorists have gone to great trouble to eliminate the necessity of using them in proofs. (A fine example is A. M. H. Gerards' short proof (1989) of Tutte's characterization of regular matroids.)
and generalized to matroids Tutte's "dichromate", a graphic polynomial now known as the Tutte polynomial
Tutte polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
(named by Crapo). Their work has recently been followed by a flood of papers—though not as many as on the Tutte polynomial of a graph.
In 1976 Dominic Welsh published the first comprehensive book on matroid theory.
Paul Seymour's decomposition theorem for regular matroids (1980) was the most significant and influential work of the late 1970s and the 1980s.
Another fundamental contribution, by , showed why projective geometries and Dowling geometries play such an important role in matroid theory.
By this time there were many other important contributors, but one should not omit to mention Geoff Whittle's extension to ternary matroids of Tutte's characterization of binary matroids that are representable over the rationals , perhaps the biggest single contribution of the 1990s. In the current decade the Matroid Minors Project of Geelen
Jim Geelen
James F. Geelen is a professor at the Department of Combinatorics and Optimization in the faculty of mathematics at the University of Waterloo, where he holds the Canada Research Chair in Combinatorial optimization. He is known for his work on Matroid theory and the extension of the Graph Minors...
, Gerards, Whittle, and others, which attempts to duplicate for matroids that are representable over a finite field the success of the Robertson–Seymour Graph Minors Project (see Robertson–Seymour theorem
Robertson–Seymour theorem
In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering...
), has produced substantial advances in the structure theory of matroids. Many others have also contributed to that part of matroid theory, which is presently flourishing.
See also
- Algebraic independenceAlgebraic independenceIn abstract algebra, a subset S of a field L is algebraically independent over a subfield K if the elements of S do not satisfy any non-trivial polynomial equation with coefficients in K...
- AntimatroidAntimatroidIn mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...
- Infinite matroid
- Matroid intersectionMatroid intersectionIn combinatorial optimization, the matroid intersection problem is to find a largest common independent set in two matroids over the same ground set. If the elements of the matroid are assigned real weights, the weighted matroid intersection problem is to find a common independent set with the...
- Oriented matroidOriented matroidAn oriented matroid is a mathematical structure that abstracts the properties of directed graphs and of arrangements of vectors in a vector space over an ordered field...
- Pregeometry (model theory)
- Structural rigidityStructural rigidityIn discrete geometry and mechanics, structural rigidity is a combinatorial theory for predicting the flexibility of ensembles formed by rigid bodies connected by flexible linkages or hinges.-Definitions:...
- Tutte polynomialTutte polynomialThe Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
- Weighted matroidWeighted matroidIn combinatorics, a branch of mathematics, a weighted matroid is a matroid endowed with function with respect to which one can perform a greedy algorithm....
Researchers
Mathematicians who pioneered the study of matroids include the following:- Saunders Mac LaneSaunders Mac LaneSaunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
- Richard RadoRichard RadoRichard Rado FRS was a Jewish German mathematician. He earned two Ph.D.s: in 1933 from the University of Berlin, and in 1935 from the University of Cambridge. He was interviewed in Berlin by Lord Cherwell for a scholarship given by the chemist Sir Robert Mond which provided financial support to...
- W. T. TutteW. T. TutteWilliam Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
- B. L. van der WaerdenBartel Leendert van der WaerdenBartel Leendert van der Waerden was a Dutch mathematician and historian of mathematics....
- Hassler WhitneyHassler WhitneyHassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
Other major contributors include:
- Henry Crapo
- Jack EdmondsJack EdmondsJack R. Edmonds is a mathematician, regarded as one of the most important contributors to the field of combinatorial optimization...
- Jim GeelenJim GeelenJames F. Geelen is a professor at the Department of Combinatorics and Optimization in the faculty of mathematics at the University of Waterloo, where he holds the Canada Research Chair in Combinatorial optimization. He is known for his work on Matroid theory and the extension of the Graph Minors...
- Gian-Carlo RotaGian-Carlo RotaGian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
- P. D. Seymour
- Geoff Whittle
There is an on-line list of current researchers.
External links
- Kingan, Sandra : Matroid theory. A large bibliography of matroid papers, matroid software, and links.
- Locke, S. C. : Greedy Algorithms.
- Pagano, Steven R. : Matroids and Signed Graphs.
- Mark Hubenthal: A Brief Look At Matroids (pdf) (contain proofs for staments of this article)

