Configuration (geometry)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines
Arrangement of lines
In geometry an arrangement of lines is the partition of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.-Definition:For any...
, such that each point is incident to the same number of lines and each line is incident to the same number of points.
Although certain specific configurations had been studied earlier (for instance by Thomas Kirkman in 1849), the formal study of configurations was first introduced by Theodor Reye
Theodor Reye
Theodor Reye was a German mathematician. He contributed to geometry, particularly projective geometry and synthetic geometry. He is best known for his introduction of configurations in second edition of his book, Geometrie der Lage...
in 1876, in the second edition of his book Geometrie der Lage, in the context of a discussion of Desargues' theorem
Desargues' theorem
In projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
. Ernst Steinitz
Ernst Steinitz
Ernst Steinitz was a German mathematician.- Biography :Steinitz was born in Laurahütte , Silesia, Germany , the son of Sigismund Steinitz, a Jewish coal merchant, and his wife Auguste Cohen; he had two brothers. He studied at the University of Breslau and the University of Berlin, receiving his Ph.D...
wrote his dissertation on the subject in 1894, and they were popularized by Hilbert and Cohn-Vossen's 1932 book Anschauliche Geometrie (reprinted in English as Geometry and the Imagination).
Configurations may be studied either as concrete sets of points and lines in a specific geometry, such as the Euclidean or projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
s, or as abstract incidence structure
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
s. In the latter case they are closely related to regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
s and regular bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
s.
Notation
A configuration in the plane is denoted by (pγ ℓπ), where p is the number of points, ℓ the number of lines, γ the number of lines per point, and π the number of points per line. These numbers necessarily satisfy the equation
as this product is the number of point-line incidences.
The notation (pγ ℓπ) does not determine a projective configuration up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
incidence isomorphism
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
. For instance, there exist three different (93 93) configurations: the Pappus configuration and two less notable configurations.
For some configurations, p = ℓ and γ = π, so the notation is often condensed to avoid repetition. For example (93 93) abbreviates to (93).
Examples
- (11), the simplest possible configuration, consisting of a point incident to a line.
- (32), the triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
. Each of its three sides meets two of its three vertices, and vice versa. More generally any polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
of n sides forms a configuration of type (n2) - (43 62) and (62 43), the complete quadrangle and complete quadrilateral respectively.
- (73), the Fano planeFano planeIn finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
. This configuration exists as an abstract incidence geometry, but cannot be constructed in the Euclidean plane. - (83), the Möbius–Kantor configuration. This configuration describes two quadrilaterals that are simultaneously inscribed and circumscribed in each other. It cannot be constructed in Euclidean plane geometry but the equations defining it have nontrivial solutions in complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. - (93), the Pappus configuration.
- (94 123), the configuration of nine inflection pointInflection pointIn differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
s of a cubic curve in the complex projective plane and the twelve lines determined by pairs of these points. This configuration shares with the Fano plane the property that it contains every line through its points; configurations with this property are known as Sylvester–Gallai configurations due to the Sylvester–Gallai theoremSylvester–Gallai theoremThe Sylvester–Gallai theorem asserts that given a finite number of points in the Euclidean plane, either# all the points are collinear; or# there is a line which contains exactly two of the points.This claim was posed as a problem by...
that shows that they cannot be given real-number coordinates . - (103), the Desargues configurationDesargues' theoremIn projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
. - (153), the Cremona–Richmond configuration.
- (124 163), the Reye configuration.
Duality of configurations
The projective dual to a configuration (pγ lπ) is a configuration (lπ pγ). Thus, types of configurations come in dual pairs, except when p = l and the configuration type is self-dual.The number of (n3) configurations
The number of nonisomorphic configurations of type (n3), starting at n = 7, is given by the sequence- 1, 1, 3, 1010 (number)10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
, 3131 (number)31 is the natural number following 30 and preceding 32.- In mathematics :Thirty-one is the third Mersenne prime as well as the fourth primorial prime, and together with twenty-nine, another primorial prime, it comprises a twin prime. As a Mersenne prime, 31 is related to the perfect number 496,...
, 229229 (number)229 is the natural number between 228 and 230. It is also a prime number.The North American telephone area code 229 is assigned to the area around the city of Albany in southwestern Georgia in North America....
, 2036, 21399, 245342, ...
These numbers count configurations as abstract incidence structures, regardless of realizability .
As discusses, nine of the ten (103) configurations, and all of the (113) and (123) configurations, are realizable in the Euclidean plane, but for each n ≥ 16 there is at least one nonrealizable (n3) configuration. Gropp also points out a long-lasting error in this sequence: an 1895 paper attempted to list all (123) configurations, and found 228 of them, but the 229th configuration was not discovered until 1988.
Higher dimensions
The concept of a configuration may be generalized to higher dimensions, for instance to points and lines or planes in spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. Notable three-dimensional configurations are the Möbius configuration
Möbius configuration
In geometry, the Möbius configuration is a certain configuration in Euclidean space consisting of two mutually inscribed tetrahedra: each vertex of one tetrahedron lies on a face plane of the other tetrahedron and vice versa...
, consisting of two mutually inscribed tetrahedra, Reye's configuration, consisting of twelve points and twelve planes, with six points per plane and six planes per point, the Gray configuration
Gray graph
In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 , then discovered independently by Bouwer 1968 in reply to a question...
consisting of a 3×3×3 grid of 27 points and the 27 orthogonal lines through them, and the Schläfli double six, a configuration with 30 points, 12 lines, two lines per point, and five points per line.
A further generalization is obtained in three dimensions by considering incidences of points, lines and planes, or j-spaces (0 ≥ j > 3), where each j-space is incident with Njk k-spaces (j ≠ k). Writing
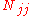for the number of j-spaces present. a given configuration may be represented by the matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
:
The principle extends generally to n dimensions, where 0 ≥ j > n. Such configurations are related mathematically to regular polytope
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s .