
Morita equivalence
Encyclopedia
In abstract algebra
, Morita equivalence is a relationship defined between rings
that preserves many ring-theoretic properties. It is named after Japanese mathematician Kiiti Morita
who defined equivalence and a similar notion of duality in 1958.
are commonly studied in terms of their modules
, as modules can be viewed as representations
of rings. Every ring has a natural R-module structure on itself where the module action is defined as the multiplication in the ring, so the approach via modules is more general and gives useful information. Because of this, one often studies a ring by studying the category
of modules over that ring.
Morita equivalence takes this viewpoint to a natural conclusion by defining rings to be equivalent if their module categories are equivalent
.
It can be shown that the left module categories R-Mod and S-Mod are equivalent if and only if the right module categories Mod-R and Mod-S are equivalent. This means that the notion of Morita equivalence does not depend on whether you are talking about left or right modules.
Equivalences can be characterized as follows: if F:R-Mod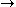 S-Mod and G:S-Mod
S-Mod and G:S-Mod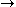 R-Mod are additive (covariant) functors, then F and G are an equivalence if and only if there is a balanced (S,R)-bimodule P such that SP and PR are finitely generated projective
R-Mod are additive (covariant) functors, then F and G are an equivalence if and only if there is a balanced (S,R)-bimodule P such that SP and PR are finitely generated projective
generators
and there are natural isomorphisms
of the functors , and of the functors
, and of the functors 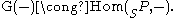
It is known that if R is Morita equivalent to S, then Cen(R) is isomorphic to Cen(S), where the Cen(-) denotes the center of the ring, and furthermore R/J(R) is Morita equivalent to S/J(S), where J(-) denotes the Jacobson radical
.
While isomorphic rings are Morita equivalent, Morita equivalent rings can be nonisomorphic. An easy example is that a division ring D is Morita equivalent to all of its matrix rings Mn(D), but cannot be isomorphic when n > 1. In the special case of commutative rings, Morita equivalent rings are actually isomorphic. This follows immediately from the comment above, for if R is Morita equivalent to S, .
.
, projective
, flat
, faithful, simple
, semisimple
, finitely generated, Artinian
, and Noetherian
. Examples of properties not necessarily preserved include being free
, and being cyclic
.
Many ring theoretic properties are stated in terms of their modules, and so it can observed that these properties are preserved between equivalent rings. Properties shared between equivalent rings are called Morita invariant properites. For example, a ring R is semisimple if and only if all of its modules are semisimple, and since semisimple modules are preserved under Morita equivalence, an equivalent ring S must also have all of its modules semisimple, and therefore be a semisimple ring itself.
Sometimes it is not immediately obvious why a property should be preserved. For example, using one standard definition of von Neumann regular ring (for all a in R, there exists x in R such that a = axa) it is not clear that an equivalent ring should also be von Neumann regular. However another formulation is: a ring is von Neumann regular if and only if all of its modules are flat. Since flatness is preserved across Morita equivalence, it is now clear that von Neumann regularity is Morita invariant.
The following properties are Morita invariant:
Examples of properties which are not Morita invariant include commutative
, local
, reduced
, domain
, right (or left) Goldie, Frobenius, invariant basis number
, and Dedekind finite.
There are at least two other tests for determining whether or not a ring property is Morita invariant. An element e in a ring R is a full idempotent when e2 = e and ReR = R.
is Morita invariant. An element e in a ring R is a full idempotent when e2 = e and ReR = R.
or
with elements in R, denoted Mn(R), is equivalent to R for any n > 0. Notice that this generalizes the classification of simple artinian rings given by Artin–Wedderburn theory
. To see the equivalence, notice that if M is a left R-module then Mn is an Mn(R)-module where the module structure is given by matrix multiplication on the left of column vectors from M. This allows the definition of a functor from the category of left R-modules to the category of left Mn(R)-modules. The inverse functor is defined by realizing that for any Mn(R)-module there is a left R-module V and a positive integer n such that the Mn(R)-module is obtained from V as described above.
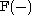 is naturally equivalent to the functor
is naturally equivalent to the functor 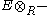 . This means that R and S are Morita equivalent if and only if there are bimodules RMS and SNR such that
. This means that R and S are Morita equivalent if and only if there are bimodules RMS and SNR such that 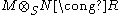 as (R,R) bimodules and
as (R,R) bimodules and 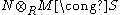 as (S,S) bimodules. Moreover, N and M are related via an (S,R) bimodule isomorphism:
as (S,S) bimodules. Moreover, N and M are related via an (S,R) bimodule isomorphism: 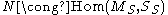 .
.
More concretely, two rings R and S are Morita equivalent if and only if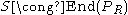 for a finitely generated projective generator module PR if and only if
for a finitely generated projective generator module PR if and only if 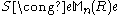 for some positive integer n and full idempotent e in the matrix ring Mn(R). A projective generator is a projective module
for some positive integer n and full idempotent e in the matrix ring Mn(R). A projective generator is a projective module
which is a generator
in the category of modules.
between the module categories, where the functors used are contravariant rather than covariant. This theory, though similar in form, has significant differences because there is no duality between the categories of modules for any rings, although dualities may exist for subcategories. In other words, because infinite dimensional modules are not generally reflexive
, the theory of dualities applies more easily to finitely generated algebras over noetherian rings. Perhaps not surprisingly, the criterion above has an analogue for dualities, where the natural isomorphism is given in terms of the hom functor rather than the tensor functor.
Morita Equivalence can also be defined in more structured situations, such as for symplectic groupoids and C*-algebras. In the case of C*-algebras, a stronger type equivalence, called strong Morita equivalence, is needed because of the additional structure to obtain results useful in applications.
of a ring is defined (in Quillen's approach) in terms of the homotopy group
s of the classifying space
of the nerve
of the category of projective modules over the ring, Morita equivalent rings must have isomorphic K-groups.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, Morita equivalence is a relationship defined between rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
that preserves many ring-theoretic properties. It is named after Japanese mathematician Kiiti Morita
Kiiti Morita
was a Japanese mathematician working in algebra and topology.He received his Ph.D. from the University of Osaka in 1950 and was professor at the University of Tsukuba....
who defined equivalence and a similar notion of duality in 1958.
Motivation
RingsRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
are commonly studied in terms of their modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, as modules can be viewed as representations
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of rings. Every ring has a natural R-module structure on itself where the module action is defined as the multiplication in the ring, so the approach via modules is more general and gives useful information. Because of this, one often studies a ring by studying the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of modules over that ring.
Morita equivalence takes this viewpoint to a natural conclusion by defining rings to be equivalent if their module categories are equivalent
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
.
Formal definition
Two rings R and S are said to be Morita equivalent (or equivalent) if there is an additive equivalence of the category of (left) modules over R, R-Mod, and the category of (left) modules over S, S-Mod. Under the equivalence functors, each R module corresponds to an S module, and vice versa.It can be shown that the left module categories R-Mod and S-Mod are equivalent if and only if the right module categories Mod-R and Mod-S are equivalent. This means that the notion of Morita equivalence does not depend on whether you are talking about left or right modules.
Equivalences can be characterized as follows: if F:R-Mod
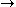 S-Mod and G:S-Mod
S-Mod and G:S-Mod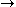 R-Mod are additive (covariant) functors, then F and G are an equivalence if and only if there is a balanced (S,R)-bimodule P such that SP and PR are finitely generated projective
R-Mod are additive (covariant) functors, then F and G are an equivalence if and only if there is a balanced (S,R)-bimodule P such that SP and PR are finitely generated projectiveProjective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
generators
Generator (category theory)
In category theory in mathematics a generator of a category \mathcal C is an object G of the category, such that for any two different morphisms f, g: X \rightarrow Y in \mathcal C, there is a morphism h : G \rightarrow X, such that the compositions f \circ h \neq g \circ h.Generators are central...
and there are natural isomorphisms
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
of the functors
 , and of the functors
, and of the functors 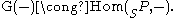
It is known that if R is Morita equivalent to S, then Cen(R) is isomorphic to Cen(S), where the Cen(-) denotes the center of the ring, and furthermore R/J(R) is Morita equivalent to S/J(S), where J(-) denotes the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
.
While isomorphic rings are Morita equivalent, Morita equivalent rings can be nonisomorphic. An easy example is that a division ring D is Morita equivalent to all of its matrix rings Mn(D), but cannot be isomorphic when n > 1. In the special case of commutative rings, Morita equivalent rings are actually isomorphic. This follows immediately from the comment above, for if R is Morita equivalent to S,
 .
.Properties preserved by equivalence
Many properties are preserved by the equivalence functor for the objects in the module category. Generally speaking, any property of modules defined purely in terms of modules and their homomorphisms (and not to their underlying elements or ring) is a categorical property which will be preserved by the equivalence functor. For example, if F(-) is the equivalence functor from R-Mod to S-Mod, then the R module M has any of the following properties if and only if the S module F(M) does: injectiveInjective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
, projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
, flat
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
, faithful, simple
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
, semisimple
Semisimple module
In mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
, finitely generated, Artinian
Artinian module
In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
, and Noetherian
Noetherian module
In abstract algebra, an Noetherian module is a module that satisfies the ascending chain condition on its submodules, where the submodules are partially ordered by inclusion....
. Examples of properties not necessarily preserved include being free
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
, and being cyclic
Cyclic module
In mathematics, more specifically in ring theory, a cyclic module is a module over a ring which is generated by one element. The term is by analogy with cyclic groups, that is groups which are generated by one element.- Definition :...
.
Many ring theoretic properties are stated in terms of their modules, and so it can observed that these properties are preserved between equivalent rings. Properties shared between equivalent rings are called Morita invariant properites. For example, a ring R is semisimple if and only if all of its modules are semisimple, and since semisimple modules are preserved under Morita equivalence, an equivalent ring S must also have all of its modules semisimple, and therefore be a semisimple ring itself.
Sometimes it is not immediately obvious why a property should be preserved. For example, using one standard definition of von Neumann regular ring (for all a in R, there exists x in R such that a = axa) it is not clear that an equivalent ring should also be von Neumann regular. However another formulation is: a ring is von Neumann regular if and only if all of its modules are flat. Since flatness is preserved across Morita equivalence, it is now clear that von Neumann regularity is Morita invariant.
The following properties are Morita invariant:
- simpleSimple ringIn abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
, semisimple - von Neumann regularVon Neumann regular ringIn mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
- right (or left) NoetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
, right (or left) ArtinianArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are... - right (or left) self-injective
- quasi-FrobeniusQuasi-Frobenius ringIn ring theory, the class of Frobenius rings and their generalizations are the extension of work done on Frobenius algebras. Perhaps the most important generalization is that of quasi-Frobenius rings , which are in turn generalized by right pseudo-Frobenius rings and right finitely...
- primePrime ringIn abstract algebra, a non-trivial ring R is a prime ring if for any two elements a and b of R, arb = 0 for all r in R implies that either a = 0 or b = 0. Prime ring can also refer to the subring of a field determined by its characteristic...
, right (or left) primitivePrimitive ringIn the branch of abstract algebra known as ring theory, a left primitive ring is a ring which has a faithful simple left module. Well known examples include endomorphism rings of vector spaces and Weyl algebras over fields of characteristic zero.- Definition :...
, semiprimeSemiprime ringIn ring theory, semiprime ideals and semiprime rings are generalizations of prime ideals and prime rings. The class of semiprime rings includes semiprimitive rings, prime rings and reduced rings....
, semiprimitiveSemiprimitive ringIn mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an... - right (or left) (semi-)hereditaryHereditary ringIn mathematics, especially in the area of abstract algebra known as module theory, a ring R is called hereditary if all submodules of projective modules over R are again projective...
- right (or left) nonsingular
- right (or left) coherentCoherent ringIn mathematics, a coherent ring is a ring in which every finitely generated left ideal is finitely presented.Many theorems about finitely generated modules over Noetherian rings can be extended to finitely presented modules over coherent rings....
- semiprimary, right (or left) perfectPerfect ringIn the area of abstract algebra known as ring theory, a left perfect ring is a type of ring in which all left modules have projective covers. The right case is defined by analogy, and the condition is not left-right symmetric, that is, there exist rings which are perfect on one side but not the...
, semiperfectSemiperfect ringIn abstract algebra, a semiperfect ring is a ring over which every finitely generated left module has a projective cover. This property is left right symmetric.- Definition :Let R be ring... - semilocal
Examples of properties which are not Morita invariant include commutative
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, local
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
, reduced
Reduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
, domain
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
, right (or left) Goldie, Frobenius, invariant basis number
Invariant basis number
In mathematics, the invariant basis number property of a ring R is the property that all free modules over R are similarly well-behaved as vector spaces, with respect to the uniqueness of their ranks.-Definition:...
, and Dedekind finite.
There are at least two other tests for determining whether or not a ring property
 is Morita invariant. An element e in a ring R is a full idempotent when e2 = e and ReR = R.
is Morita invariant. An element e in a ring R is a full idempotent when e2 = e and ReR = R. is Morita invariant if and only if whenever a ring R satisfies
is Morita invariant if and only if whenever a ring R satisfies  , then so does eRe for every full idempotent e and so does every matrix ring Mn(R) for every positive integer n;
, then so does eRe for every full idempotent e and so does every matrix ring Mn(R) for every positive integer n;
or
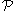 is Morita invariant if and only if: for any ring R and full idempotent e in R, R satisfies
is Morita invariant if and only if: for any ring R and full idempotent e in R, R satisfies 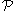 if and only if the ring eRe satisfies
if and only if the ring eRe satisfies  .
.
Examples
The ring of matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with elements in R, denoted Mn(R), is equivalent to R for any n > 0. Notice that this generalizes the classification of simple artinian rings given by Artin–Wedderburn theory
Artin–Wedderburn theorem
In abstract algebra, the Artin–Wedderburn theorem is a classification theorem for semisimple rings. The theorem states that an Artinian semisimple ring R is isomorphic to a product of finitely many ni-by-ni matrix rings over division rings Di, for some integers ni, both of which are uniquely...
. To see the equivalence, notice that if M is a left R-module then Mn is an Mn(R)-module where the module structure is given by matrix multiplication on the left of column vectors from M. This allows the definition of a functor from the category of left R-modules to the category of left Mn(R)-modules. The inverse functor is defined by realizing that for any Mn(R)-module there is a left R-module V and a positive integer n such that the Mn(R)-module is obtained from V as described above.
Criterion for equivalence
For every right-exact functor F from the category of left-R modules to the category of left-S modules that commutes with direct sums, a theorem of homological algebra shows that there is a (S,R)-bimodule E such that the functor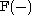 is naturally equivalent to the functor
is naturally equivalent to the functor 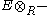 . This means that R and S are Morita equivalent if and only if there are bimodules RMS and SNR such that
. This means that R and S are Morita equivalent if and only if there are bimodules RMS and SNR such that 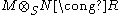 as (R,R) bimodules and
as (R,R) bimodules and 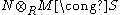 as (S,S) bimodules. Moreover, N and M are related via an (S,R) bimodule isomorphism:
as (S,S) bimodules. Moreover, N and M are related via an (S,R) bimodule isomorphism: 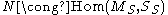 .
.More concretely, two rings R and S are Morita equivalent if and only if
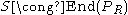 for a finitely generated projective generator module PR if and only if
for a finitely generated projective generator module PR if and only if 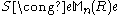 for some positive integer n and full idempotent e in the matrix ring Mn(R). A projective generator is a projective module
for some positive integer n and full idempotent e in the matrix ring Mn(R). A projective generator is a projective moduleProjective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
which is a generator
Generator (category theory)
In category theory in mathematics a generator of a category \mathcal C is an object G of the category, such that for any two different morphisms f, g: X \rightarrow Y in \mathcal C, there is a morphism h : G \rightarrow X, such that the compositions f \circ h \neq g \circ h.Generators are central...
in the category of modules.
Further directions
Dual to the theory of equivalences is the theory of dualitiesOpposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
between the module categories, where the functors used are contravariant rather than covariant. This theory, though similar in form, has significant differences because there is no duality between the categories of modules for any rings, although dualities may exist for subcategories. In other words, because infinite dimensional modules are not generally reflexive
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
, the theory of dualities applies more easily to finitely generated algebras over noetherian rings. Perhaps not surprisingly, the criterion above has an analogue for dualities, where the natural isomorphism is given in terms of the hom functor rather than the tensor functor.
Morita Equivalence can also be defined in more structured situations, such as for symplectic groupoids and C*-algebras. In the case of C*-algebras, a stronger type equivalence, called strong Morita equivalence, is needed because of the additional structure to obtain results useful in applications.
Significance in K-theory
If two rings are Morita equivalent, there is an induced equivalence of the respective categories of projective modules since the Morita equivalences will preserve exact sequences (and hence projective modules). Since the algebraic K-theoryAlgebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
of a ring is defined (in Quillen's approach) in terms of the homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of the classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
of the nerve
Nerve (category theory)
In category theory, the nerve N of a small category C is a simplicial set constructed from the objects and morphisms of C. The geometric realization of this simplicial set is a topological space, called the classifying space of the category C...
of the category of projective modules over the ring, Morita equivalent rings must have isomorphic K-groups.

