
Semiprime ring
Encyclopedia
In ring theory
, semiprime ideal
s and semiprime ring
s are generalizations of prime ideal
s and prime ring
s. The class of semiprime rings includes semiprimitive ring
s, prime ring
s and reduced ring
s.
In commutative algebra
, semiprime ideals are also called radical ideals.
Most definitions and assertions in this article appear in and .
As with prime ideals, this is extended to noncommutative rings "ideal-wise". The following conditions are equivalent definitions for a semiprime ideal A in a ring R:
The ring R is called a semiprime ring if the zero ideal is a semiprime ideal. In the commutative case, this is equivalent to R being a reduced ring
, since R has no nonzero nilpotent elements. In the noncommutative case, the ring merely has no nonzero nilpotent right ideals. So while a reduced ring is always semiprime, the converse is not true.
is prime.
While the intersection of prime ideals is not usually prime, it is a semiprime ideal. Shortly it will be shown that the converse is also true, that every semiprime ideal is the intersection of a family of prime ideals.
For any ideal B in a ring R, we can form the following sets:
The set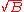 is the definition of the radical of B
is the definition of the radical of B
and is clearly a semiprime ideal containing B, and in fact is the smallest semiprime ideal containing B. The inclusion above is sometimes proper in the general case, but for commutative rings it becomes an equality.
With this definition, an ideal A is semiprime if and only if . At this point, it is also apparent that every semiprime ideal is in fact the intersection of a family of prime ideals. Moreover, this shows that the intersection of any two semiprime ideals is again semiprime.
. At this point, it is also apparent that every semiprime ideal is in fact the intersection of a family of prime ideals. Moreover, this shows that the intersection of any two semiprime ideals is again semiprime.
By definition R is semiprime if and only if , that is, the intersection of all prime ideals is zero. This ideal
, that is, the intersection of all prime ideals is zero. This ideal  is also denoted by
is also denoted by 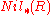 and also called Baer's lower nilradical or the Baer-Mccoy radical or the prime radical of R.
and also called Baer's lower nilradical or the Baer-Mccoy radical or the prime radical of R.
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, semiprime ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
s and semiprime ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s are generalizations of prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s and prime ring
Prime ring
In abstract algebra, a non-trivial ring R is a prime ring if for any two elements a and b of R, arb = 0 for all r in R implies that either a = 0 or b = 0. Prime ring can also refer to the subring of a field determined by its characteristic...
s. The class of semiprime rings includes semiprimitive ring
Semiprimitive ring
In mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an...
s, prime ring
Prime ring
In abstract algebra, a non-trivial ring R is a prime ring if for any two elements a and b of R, arb = 0 for all r in R implies that either a = 0 or b = 0. Prime ring can also refer to the subring of a field determined by its characteristic...
s and reduced ring
Reduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
s.
In commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, semiprime ideals are also called radical ideals.
Most definitions and assertions in this article appear in and .
Definitions
For a commutative ring R, an ideal A is a semiprime ideal if A satsifies either of the following equivalent conditions:- If xk is in A for some positive integer k and element x of R, then x is in A.
- If y is in R but not in A, all positive integer powers of y are not in A.
As with prime ideals, this is extended to noncommutative rings "ideal-wise". The following conditions are equivalent definitions for a semiprime ideal A in a ring R:
- If Jk⊆A for a positive natural number k and ideal J of R, then J⊆A.
- If Jk⊆A for a positive natural number k and right ideal J of R, then J⊆A.
- If Jk⊆A for a positive natural number k and left ideal J of R, then J⊆A.
- If xRx⊆A for some x in R, then x is in A.
The ring R is called a semiprime ring if the zero ideal is a semiprime ideal. In the commutative case, this is equivalent to R being a reduced ring
Reduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
, since R has no nonzero nilpotent elements. In the noncommutative case, the ring merely has no nonzero nilpotent right ideals. So while a reduced ring is always semiprime, the converse is not true.
General properties of semiprime ideals
To begin with, it is clear that prime ideals are semiprime, and that for commutative rings, a semiprime primary idealPrimary ideal
In mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
is prime.
While the intersection of prime ideals is not usually prime, it is a semiprime ideal. Shortly it will be shown that the converse is also true, that every semiprime ideal is the intersection of a family of prime ideals.
For any ideal B in a ring R, we can form the following sets:

The set
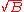 is the definition of the radical of B
is the definition of the radical of BRadical of an ideal
In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
and is clearly a semiprime ideal containing B, and in fact is the smallest semiprime ideal containing B. The inclusion above is sometimes proper in the general case, but for commutative rings it becomes an equality.
With this definition, an ideal A is semiprime if and only if
 . At this point, it is also apparent that every semiprime ideal is in fact the intersection of a family of prime ideals. Moreover, this shows that the intersection of any two semiprime ideals is again semiprime.
. At this point, it is also apparent that every semiprime ideal is in fact the intersection of a family of prime ideals. Moreover, this shows that the intersection of any two semiprime ideals is again semiprime.By definition R is semiprime if and only if
 , that is, the intersection of all prime ideals is zero. This ideal
, that is, the intersection of all prime ideals is zero. This ideal  is also denoted by
is also denoted by 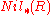 and also called Baer's lower nilradical or the Baer-Mccoy radical or the prime radical of R.
and also called Baer's lower nilradical or the Baer-Mccoy radical or the prime radical of R.
