
Semisimple module
Encyclopedia
In mathematics
, especially in the area of abstract algebra
known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring
which is a semisimple module over itself is known as an artinian semisimple ring. Some important rings, such as group ring
s of finite group
s over fields
of characteristic zero, are semisimple rings. An artinian ring
is initially understood via its largest semisimple quotient. The structure of artinian semisimple rings is well understood by the Artin–Wedderburn theorem
, which exhibits these rings as finite direct product
s of matrix ring
s.
over a (not necessarily commutative) ring with unity is said to be semisimple (or completely reducible) if it is the direct sum
of simple
(irreducible) submodules.
For a module M, the following are equivalent:
For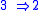 , the starting idea is to find an irreducible submodule by picking any
, the starting idea is to find an irreducible submodule by picking any 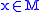 and letting
and letting  be a maximal submodule such that
be a maximal submodule such that 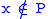 . It can be shown that the complement of
. It can be shown that the complement of  is irreducible.
is irreducible.
Semisimple is stronger than completely decomposable
,
which is a direct sum
of indecomposable submodules
.
Semisimple rings are of particular interest to algebraists. For example, if the base ring R is semisimple, then all R-modules would automatically be semisimple. Furthermore, every simple (left) R-module is isomorphic to a minimal left ideal of R.
Semisimple rings are both Artinian
and Noetherian
. From the above properties, a ring is semisimple if and only if it is Artinian and its radical
is zero.
If an Artinian semisimple ring contains a field, it is called a semisimple algebra
.
Classic examples of simple, but not semisimple, rings are the Weyl algebras, such as Q<x,y>/(xy-yx-1) which is a simple noncommutative domain
. These and many other nice examples are discussed in more detail in several noncommutative ring theory texts, including chapter 3 of Lam's text, in which they are described as nonartinian simple rings. The module theory for the Weyl algebras is well studied and differs significantly from that of semisimple rings.
) if the intersection of the maximal left ideals is zero, that is, if the Jacobson radical
is zero. Every ring which is semisimple as a module over itself has zero Jacobson radical, but not every ring with zero Jacobson radical is semisimple as a module over itself. A J-semisimple ring is semisimple if and only if it is an artinian ring
, so semisimple rings are often called artinian semisimple rings to avoid confusion.
For example the ring of integers, Z, is J-semisimple, but not artinian semisimple.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
which is a semisimple module over itself is known as an artinian semisimple ring. Some important rings, such as group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
s of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s over fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic zero, are semisimple rings. An artinian ring
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
is initially understood via its largest semisimple quotient. The structure of artinian semisimple rings is well understood by the Artin–Wedderburn theorem
Artin–Wedderburn theorem
In abstract algebra, the Artin–Wedderburn theorem is a classification theorem for semisimple rings. The theorem states that an Artinian semisimple ring R is isomorphic to a product of finitely many ni-by-ni matrix rings over division rings Di, for some integers ni, both of which are uniquely...
, which exhibits these rings as finite direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
s of matrix ring
Matrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
s.
Definition
A moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a (not necessarily commutative) ring with unity is said to be semisimple (or completely reducible) if it is the direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of simple
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
(irreducible) submodules.
For a module M, the following are equivalent:
- M is a direct sum of irreducible modules.
- M is the sum of its irreducible submodules.
- Every submodule of M is a direct summand: for every submodule N of M, there is a complement P such that M = N ⊕ P.
For
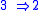 , the starting idea is to find an irreducible submodule by picking any
, the starting idea is to find an irreducible submodule by picking any 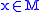 and letting
and letting  be a maximal submodule such that
be a maximal submodule such that 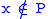 . It can be shown that the complement of
. It can be shown that the complement of  is irreducible.
is irreducible.Semisimple is stronger than completely decomposable
Indecomposable module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
,
which is a direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of indecomposable submodules
Indecomposable module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
.
Properties
- If M is semisimple and N is a submodule, then N and M/N are also semisimple.
- If each
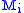 is a semisimple module, then so is
is a semisimple module, then so is 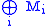 .
. - A module M is finitely generated and semisimple if and only if it is Artinian and its radicalRadical of a moduleIn mathematics, in the theory of modules, the radical of a module is a component in the theory of structure and classification. It is a generalization of the Jacobson radical for rings. In many ways, it is the dual notion to that of the socle soc of M.-Definition:Let R be a ring and M a left...
is zero.
Endomorphism rings
- A semisimple module M over a ring R can also be thought of as a ring homomorphismRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
from R into the ring of abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
endomorphismEndomorphismIn mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s of M. The image of this homomorphism is a semiprimitive ringSemiprimitive ringIn mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an...
, and every semiprimitive ring is isomorphic to such an image. - The endomorphism ringEndomorphism ringIn abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of a semisimple module is not only semiprimitive, but also von Neumann regularVon Neumann regular ringIn mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
, .
Semisimple rings
A ring is said to be (left)-semisimple if it is semisimple as a left module over itself. Surprisingly, a left-semisimple ring is also right-semisimple and vice versa. The left/right distinction is therefore unnecessary, and one can speak of semisimple rings without ambiguity.Semisimple rings are of particular interest to algebraists. For example, if the base ring R is semisimple, then all R-modules would automatically be semisimple. Furthermore, every simple (left) R-module is isomorphic to a minimal left ideal of R.
Semisimple rings are both Artinian
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
and Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
. From the above properties, a ring is semisimple if and only if it is Artinian and its radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
is zero.
If an Artinian semisimple ring contains a field, it is called a semisimple algebra
Semisimple algebra
In ring theory, a semisimple algebra is an associative algebra which has trivial Jacobson radical...
.
Examples
- If k is a field and G is a finite group of order n, then the group ringGroup ringIn algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
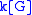 is semisimple if and only if the characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
is semisimple if and only if the characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of k does not divide n. This is Maschke's theoremMaschke's theoremIn mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
, an important result in group representation theory. - By the Artin–Wedderburn theoremArtin–Wedderburn theoremIn abstract algebra, the Artin–Wedderburn theorem is a classification theorem for semisimple rings. The theorem states that an Artinian semisimple ring R is isomorphic to a product of finitely many ni-by-ni matrix rings over division rings Di, for some integers ni, both of which are uniquely...
, a unital ring R is semisimple if and only if it is (isomorphic to)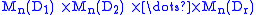 , where each
, where each 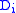 is a division ringDivision ringIn abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
is a division ringDivision ringIn abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
and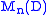 is the ring of n-by-n matrices with entries in D.
is the ring of n-by-n matrices with entries in D. - An example of a semisimple non-unital ring is
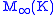 , the row-finite, column-finite, infinite matrices over a field K.
, the row-finite, column-finite, infinite matrices over a field K.
Simple rings
One should beware that despite the terminology, not all simple rings are semisimple. The problem is that the ring may be "too big", that is, not (left/right) Artinian. In fact, if R is a simple ring with a minimal left/right ideal, then R is semisimple.Classic examples of simple, but not semisimple, rings are the Weyl algebras, such as Q<x,y>/(xy-yx-1) which is a simple noncommutative domain
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
. These and many other nice examples are discussed in more detail in several noncommutative ring theory texts, including chapter 3 of Lam's text, in which they are described as nonartinian simple rings. The module theory for the Weyl algebras is well studied and differs significantly from that of semisimple rings.
Jacobson semisimple
A ring is called Jacobson semisimple (or J-semisimple or semiprimitiveSemiprimitive ring
In mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an...
) if the intersection of the maximal left ideals is zero, that is, if the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
is zero. Every ring which is semisimple as a module over itself has zero Jacobson radical, but not every ring with zero Jacobson radical is semisimple as a module over itself. A J-semisimple ring is semisimple if and only if it is an artinian ring
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
, so semisimple rings are often called artinian semisimple rings to avoid confusion.
For example the ring of integers, Z, is J-semisimple, but not artinian semisimple.
Textbooks
| year=2001}}- R.S. Pierce. Associative Algebras. Graduate Texts in Mathematics vol 88.

