
Light field
Encyclopedia
The light field is a function that describes the amount of light
faring in every direction through every point in space. Michael Faraday
was the first to propose (in an 1846
lecture entitled "Thoughts on Ray Vibrations") that light should be interpreted as a field, much like the magnetic fields on which he had been working for several years. The phrase light field was coined by Alexander Gershun in a classic paper on the radiometric properties of light in three-dimensional space (1936). The phrase has been redefined by researchers in computer graphics
to mean something slightly different.
—i.e. to incoherent light and to objects larger than the wavelength of light—then the fundamental carrier of light is a ray
. The measure for the amount of light faring along a ray is radiance
, denoted by L and measured in watt
s (W) per steradian
(sr) per meter squared (m2). The steradian is a measure of solid angle
, and meters squared are used here as a measure of cross-sectional area, as shown at right.
The radiance along all such rays in a region of three-dimensional space illuminated by an unchanging arrangement of lights is called the plenoptic function (Adelson 1991). The plenoptic illumination function is an idealized function used in computer vision
and computer graphics
to express the image of a scene from any possible viewing position at any viewing angle at any point in time. It is never actually used in practice, and is more useful in understanding other concepts in vision and graphics. Since rays in space can be parameterized by three coordinates, x, y, and z and two angles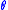 and
and  , as shown at left, it is a five-dimensional function. (One can consider time, wavelength
, as shown at left, it is a five-dimensional function. (One can consider time, wavelength
, and polarization angle as additional variables, yielding higher-dimensional functions.)
Like Adelson, Gershun defined the light field at each point in space as a 5D function. However, he treated it as an infinite collection of vectors, one per direction impinging on the point, with lengths proportional to their radiances.
Integrating these vectors over any collection of lights, or over the entire sphere of directions, produces a single scalar value - the total irradiance at that point, and a resultant direction. The figure at right, reproduced from Gershun's paper, shows this calculation for the case of two light sources. In computer graphics, this vector-valued function of 3D space is called the vector irradiance field (Arvo, 1994). The vector direction at each point in the field can be interpreted as the orientation one would face a flat surface placed at that point to most brightly illuminate it.
Note that a light slab does not mean that the 4D light field is equivalent to capturing two 2D planes of information (this latter is only two dimensional). For example, a pair of points at position (0,0) in the st plane and (1,1) in the uv plane correspond to a ray in space, but other rays may pass through (0,0) in the st plane and through (1,1) in the uv plane – this pair of points correspond only to the one ray, not all these other rays.
, and the corresponding parametrization is the Kirchhoff-Helmholtz integral, which states that, in the absence of obstacles, a sound field over time is given by the pressure on a plane. Thus this is 2D of information at any point, and over time a 3D field.
This 2D, compared with the 4D of light, is because light travels in rays (0D at a point in time, 1D over time), while by Huygens' Principle, a sound wave front can be modeled as spherical waves (2D at a point in time, 3D over time): light moves in a single direction (2D of information), while sound simply expands in every direction.
In computer graphics, light fields are typically produced either by rendering
a 3D model or by photographing a real scene. In either case,
to produce a light field views must be obtained for a large collection of viewpoints. Depending on the parameterization employed, this collection will typically span some portion of a line, circle, plane, sphere, or other shape, although unstructured collections of viewpoints are also possible (Buehler 2001).
Devices for capturing light fields photographically may include a moving handheld camera, a robotically controlled camera (Levoy, 2002) an arc of
cameras (as in the bullet time
effect used in The Matrix
), a dense array of cameras (Kanade 1998; Yang 2002; Wilburn 2005), or a handheld camera (Ng
2005; Georgiev 2006), microscope (Levoy 2006), or other optical system in which an array of microlenses has been inserted in the optical path.
How many images should be in a light field? The largest known light field (of Michelangelo's statue of Night) contains 24,000 1.3-megapixel images. At a deeper level, the answer depends on the application. For light field
rendering (see the Application section below), if you want to walk completely around an opaque object, then of course you need to photograph its back side. Less obviously, if you want to walk close to the object, and the object lies astride the st plane, then you need images taken at finely spaced positions on the uv plane (in the two-plane parameterization shown above), which is now behind you, and these images need to have high spatial resolution.
The number and arrangement of images in a light field, and the resolution of each image, are together called the "sampling" of the 4D light field. Analyses of light field sampling have been undertaken by many researchers; a good starting point is Chai (2000). Also of interest is Durand (2005) for the effects of occlusion, Ramamoorthi (2006) for the effects of lighting and reflection, and Ng
(2005) and Zwicker (2006) for applications to plenoptic camera
s and 3D displays, respectively.
wavelengths, and many of those produce light fields. As a result, listing all applications of light fields would require surveying all uses of computational imaging in art, science, engineering, and medicine. In computer graphics, some selected applications are:
Illumination engineering. Gershun's reason for studying the light field was to derive (in closed form if possible) the illumination patterns that would be observed on surfaces due to light sources of various shapes positioned above these surface. An example is shown at right. A more modern study is (Ashdown 1993).
Light field rendering. By extracting appropriate 2D slices from the 4D light field of a scene, one can produce novel views of the scene (Levoy 1996; Gortler 1996). Depending on the parameterization of the light field and slices, these views might be perspective, orthographic
, crossed-slit (Zomet 2003), multi-perspective (Rademacher 1998), or another type of projection. Light field rendering is one form of image-based rendering
.
Synthetic aperture photography. By integrating an appropriate 4D subset of the samples in a light field, one can approximate the view that would be captured by a camera having a finite (i.e. non-pinhole) aperture. Such a view has a finite depth of field
. By shearing or warping the light field before performing this integration, one can focus on different fronto-parallel (Isaksen 2000) or oblique (Vaish 2005) planes in the scene. If the light field is captured using a handheld camera (Ng
2005), this essentially constitutes a digital camera whose photographs can be refocused after they are taken.
3D display. By presenting a light field using technology that maps each sample to the appropriate ray in physical space, one obtains an
autostereoscopic
visual effect akin to viewing the original scene. Non-digital technologies for doing this include integral photography, parallax panoramagrams
, and holography
; digital technologies include placing an array of lenslets over a high-resolution display screen, or projecting the imagery onto an array of lenslets using an array of video projectors. If the latter is combined with an array of video cameras, one can capture and display a time-varying light field. This essentially constitutes a 3D television system (Javidi 2002; Matusik 2004).
Image generation and predistortion of synthetic imagery for holographic stereograms is one of the earliest examples of computed light fields, anticipating and later motivating the geometry used in Levoy and Hanrahan's work (Halle 1991, 1994).
Glare reduction. Glare arises due to multiple scattering of light inside the camera’s body and lens optics and reduces image contrast. While glare has been analyzed in 2D image space (Talvala 2007), it is useful to identify it as a 4D ray-space phenomenon (Raskar 2008). By statistically analyzing the ray-space inside a camera, one can classify and remove glare artifacts. In ray-space, glare behaves as high frequency noise and can be reduced by outlier rejection. Such analysis can be performed by capturing the light field inside the camera, but it results in the loss of spatial resolution. Uniform and non-uniform ray sampling could be used to reduce glare without significantly compromising image resolution (Raskar 2008).
Adelson, E.H., Bergen, J.R. (1991).
"The plenoptic function and the elements of early vision",
In Computation Models of Visual Processing,
M. Landy and J.A. Movshon, eds., MIT Press, Cambridge, 1991, pp. 3–20.
Arvo, J. (1994).
"The Irradiance Jacobian for Partially Occluded Polyhedral Sources",
Proc. ACM SIGGRAPH,
ACM Press, pp. 335–342.
Faraday, M.,
"Thoughts on Ray Vibrations",
Philosophical Magazine,
S.3, Vol XXVIII, N188, May 1846.
Gershun, A. (1936).
"The Light Field",
Moscow, 1936. Translated by P. Moon and G. Timoshenko in
Journal of Mathematics and Physics,
Vol. XVIII, MIT, 1939, pp. 51–151.
Gortler, S.J., Grzeszczuk, R., Szeliski, R., Cohen, M. (1996).
"The Lumigraph",
Proc. ACM SIGGRAPH,
ACM Press, pp. 43–54.
Levoy, M., Hanrahan, P. (1996).
"Light Field Rendering",
Proc. ACM SIGGRAPH,
ACM Press, pp. 31–42.
Moon, P., Spencer, D.E. (1981).
The Photic Field,
MIT Press.
Wigner Distribution Function and Light Fields
Ramamoorthi, R., Mahajan, D., Belhumeur, P. (2006).
"A First Order Analysis of Lighting, Shading, and Shadows",
ACM TOG.
Zwicker, M., Matusik, W., Durand, F., Pfister, H. (2006).
"Antialiasing for Automultiscopic 3D Displays",
Eurographics Symposium on Rendering, 2006.
Ng, R. (2005).
"Fourier Slice Photography",
Proc. ACM SIGGRAPH, ACM Press, pp. 735–744.
Durand, F., Holzschuch, N., Soler, C., Chan, E., Sillion, F. X. (2005).
"A Frequency analysis of Light Transport",
Proc. ACM SIGGRAPH, ACM Press, pp. 1115–1126.
Chai, J.-X., Tong, X., Chan, S.-C., Shum, H. (2000).
"Plenoptic Sampling",
Proc. ACM SIGGRAPH, ACM Press, pp. 307–318.
Halle, M. (1994)
"Holographic stereograms as discrete imaging systems",
in SPIE Proc. Vol. #2176: Practical Holography VIII, S.A. Benton, ed., pp. 73–84.
Liang, C.K., Lin, T.H., Wong, B.Y., Liu, C., Chen, H. H. (2008).
"Programmable Aperture Photography:Multiplexed Light Field Acquisition", Proc. ACM SIGGRAPH.
Veeraraghavan, A., Raskar, R., Agrawal, A., Mohan, A., Tumblin, J. (2007).
"Dappled Photography: Mask Enhanced Cameras for Heterodyned Light Fields and Coded Aperture Refocusing", Proc. ACM SIGGRAPH.
Georgiev, T., Zheng, C., Nayar, S., Curless, B., Salesin, D., Intwala, C. (2006).
"Spatio-angular Resolution Trade-offs in Integral Photography", Proc. EGSR 2006.
Kanade, T., Saito, H., Vedula, S. (1998).
"The 3D Room: Digitizing Time-Varying 3D Events by Synchronized Multiple Video Streams", Tech report CMU-RI-TR-98-34, December 1998.
Levoy, M. (2002).
Stanford Spherical Gantry.
Levoy, M., Ng, R., Adams, A., Footer, M., Horowitz, M. (2006).
"Light field microscopy",
ACM Transactions on Graphics (Proc. SIGGRAPH),
Vol. 25, No. 3.
Ng, R., Levoy, M., Brédif, M., Duval, G., Horowitz, M., Hanrahan, P. (2005).
"Light Field Photography with a Hand-Held Plenoptic Camera", Stanford Tech Report CTSR 2005-02, April, 2005.
Wilburn, B., Joshi, N., Vaish, V., Talvala, E., Antunez, E., Barth, A., Adams, A., Levoy, M., Horowitz, M. (2005).
"High Performance Imaging Using Large Camera Arrays",
ACM Transactions on Graphics (Proc. SIGGRAPH),
Vol. 24, No. 3, pp. 765–776.
Yang, J.C., Everett, M., Buehler, C., McMillan, L. (2002).
"A real-time distributed light field camera",
Proc. Eurographics Rendering Workshop 2002.
"The CAFADIS camera"
"The Stanford Light Field Archive"
"UCSD/MERL Light Field Repository"
Ashdown, I. (1993).
"Near-Field Photometry: A New Approach",
Journal of the Illuminating Engineering Society,
Vol. 22, No. 1, Winter, 1993, pp. 163–180.
Buehler, C., Bosse, M., McMillan, L., Gortler, S., Cohen, M. (2001).
"Unstructured Lumigraph rendering",
Proc. ACM SIGGRAPH,
ACM Press.
Isaksen, A., McMillan, L., Gortler, S.J. (2000).
"Dynamically Reparameterized Light Fields", Proc. ACM SIGGRAPH, ACM Press, pp. 297–306.
Javidi, B., Okano, F., eds. (2002).
Three-Dimensional Television, Video and Display Technologies,
Springer-Verlag.
Matusik, W., Pfister, H. (2004).
"3D TV: a scalable system for real-time acquisition, transmission, and autostereoscopic display of dynamic scenes",
Proc. ACM SIGGRAPH, ACM Press.
Rademacher, P., Bishop, G. (1998).
"Multiple-Center-of-Projection Images",
Proc. ACM SIGGRAPH,
ACM Press.
Vaish, V., Garg, G., Talvala, E., Antunez, E., Wilburn, B.,
Horowitz, M., Levoy, M. (2005).
"Synthetic Aperture Focusing using a Shear-Warp Factorization of the Viewing Transform",
Proc. Workshop on Advanced 3D Imaging for Safety and Security,
in conjunction with CVPR 2005.
Zomet, A., Feldman, D., Peleg, S., Weinshall, D. (2003).
"Mosaicing new views: the crossed-slits projection",
IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI),
Vol. 25, No. 6, June 2003, pp. 741–754.
Halle, M., Benton, S., Klug, M., Underkoffler, J. (1991).
"The UltraGram: a generalized holographic stereogram",
SPIE Vol. 1461, Practical Holography V, S.A. Benton, ed., pp. 142–155.
Talvala, E-V., Adams, A., Horowitz, M., Levoy, M. (2007).
"Veiling glare in high dynamic range imaging",
Proc. ACM SIGGRAPH.
Raskar, R., Agrawal, A., Wilson, C., Veeraraghavan, A. (2008).
"Glare Aware Photography: 4D Ray Sampling for Reducing Glare Effects of Camera Lenses",
Proc. ACM SIGGRAPH.
Pérez, F., Marichal, J. G., Rodriguez, J.M. (2008).
"The Discrete Focal Stack Transform",
Proc. EUSIPCO
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
faring in every direction through every point in space. Michael Faraday
Michael Faraday
Michael Faraday, FRS was an English chemist and physicist who contributed to the fields of electromagnetism and electrochemistry....
was the first to propose (in an 1846
1846 in science
The year 1846 in science and technology involved some significant events, listed below.-Astronomy:* February 20 - Francesco de Vico discovers comet 122P/de Vico....
lecture entitled "Thoughts on Ray Vibrations") that light should be interpreted as a field, much like the magnetic fields on which he had been working for several years. The phrase light field was coined by Alexander Gershun in a classic paper on the radiometric properties of light in three-dimensional space (1936). The phrase has been redefined by researchers in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
to mean something slightly different.
The 5D plenoptic function
If the concept is restricted to geometric opticsOptics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
—i.e. to incoherent light and to objects larger than the wavelength of light—then the fundamental carrier of light is a ray
Ray (optics)
In optics, a ray is an idealized narrow beam of light. Rays are used to model the propagation of light through an optical system, by dividing the real light field up into discrete rays that can be computationally propagated through the system by the techniques of ray tracing. This allows even very...
. The measure for the amount of light faring along a ray is radiance
Radiance
Radiance and spectral radiance are radiometric measures that describe the amount of radiation such as light or radiant heat that passes through or is emitted from a particular area, and falls within a given solid angle in a specified direction. They are used to characterize both emission from...
, denoted by L and measured in watt
Watt
The watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
s (W) per steradian
Steradian
The steradian is the SI unit of solid angle. It is used to describe two-dimensional angular spans in three-dimensional space, analogous to the way in which the radian describes angles in a plane...
(sr) per meter squared (m2). The steradian is a measure of solid angle
Solid angle
The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
, and meters squared are used here as a measure of cross-sectional area, as shown at right.
The radiance along all such rays in a region of three-dimensional space illuminated by an unchanging arrangement of lights is called the plenoptic function (Adelson 1991). The plenoptic illumination function is an idealized function used in computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
and computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
to express the image of a scene from any possible viewing position at any viewing angle at any point in time. It is never actually used in practice, and is more useful in understanding other concepts in vision and graphics. Since rays in space can be parameterized by three coordinates, x, y, and z and two angles
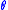 and
and  , as shown at left, it is a five-dimensional function. (One can consider time, wavelength
, as shown at left, it is a five-dimensional function. (One can consider time, wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
, and polarization angle as additional variables, yielding higher-dimensional functions.)
Like Adelson, Gershun defined the light field at each point in space as a 5D function. However, he treated it as an infinite collection of vectors, one per direction impinging on the point, with lengths proportional to their radiances.
Integrating these vectors over any collection of lights, or over the entire sphere of directions, produces a single scalar value - the total irradiance at that point, and a resultant direction. The figure at right, reproduced from Gershun's paper, shows this calculation for the case of two light sources. In computer graphics, this vector-valued function of 3D space is called the vector irradiance field (Arvo, 1994). The vector direction at each point in the field can be interpreted as the orientation one would face a flat surface placed at that point to most brightly illuminate it.
The 4D light field
In a plenoptic function, if the region of interest contains a concave object (think of a cupped hand), then light leaving one point on the object may fare only narrowly until being blocked by another point on the object. No practical device could measure the function in such a region.Note that a light slab does not mean that the 4D light field is equivalent to capturing two 2D planes of information (this latter is only two dimensional). For example, a pair of points at position (0,0) in the st plane and (1,1) in the uv plane correspond to a ray in space, but other rays may pass through (0,0) in the st plane and through (1,1) in the uv plane – this pair of points correspond only to the one ray, not all these other rays.
Sound analog
The analog of the 4D light field for sound is the sound field or wave field, as in wave field synthesisWave field synthesis
Wave field synthesis is a spatial audio rendering technique, characterized by creation of virtual acoustic environments. It produces "artificial" wave fronts synthesized by a large number of individually driven speakers. Such wave fronts seem to originate from a virtual starting point, the virtual...
, and the corresponding parametrization is the Kirchhoff-Helmholtz integral, which states that, in the absence of obstacles, a sound field over time is given by the pressure on a plane. Thus this is 2D of information at any point, and over time a 3D field.
This 2D, compared with the 4D of light, is because light travels in rays (0D at a point in time, 1D over time), while by Huygens' Principle, a sound wave front can be modeled as spherical waves (2D at a point in time, 3D over time): light moves in a single direction (2D of information), while sound simply expands in every direction.
Ways to create light fields
Light fields are a fundamental representation for light. As such, there are as many ways of creating light fields as there are computer programs capable of creating images or instruments capable of capturing them.In computer graphics, light fields are typically produced either by rendering
Rendering (computer graphics)
Rendering is the process of generating an image from a model , by means of computer programs. A scene file contains objects in a strictly defined language or data structure; it would contain geometry, viewpoint, texture, lighting, and shading information as a description of the virtual scene...
a 3D model or by photographing a real scene. In either case,
to produce a light field views must be obtained for a large collection of viewpoints. Depending on the parameterization employed, this collection will typically span some portion of a line, circle, plane, sphere, or other shape, although unstructured collections of viewpoints are also possible (Buehler 2001).
Devices for capturing light fields photographically may include a moving handheld camera, a robotically controlled camera (Levoy, 2002) an arc of
cameras (as in the bullet time
Bullet time
Bullet time is a special and visual effect that refers to a digitally enhanced simulation of variable-speed photography used in films, broadcast advertisements, and video games...
effect used in The Matrix
The Matrix
The Matrix is a 1999 science fiction-action film written and directed by Larry and Andy Wachowski, starring Keanu Reeves, Laurence Fishburne, Carrie-Anne Moss, Joe Pantoliano, and Hugo Weaving...
), a dense array of cameras (Kanade 1998; Yang 2002; Wilburn 2005), or a handheld camera (Ng
Ren Ng
Dr. Ren Ng is the founder and the chief executive officer of a Mountain View, California-based start-up, Lytro, Inc. . The company is developing light field technology for digital cameras and has received $50 million in venture capital funding..Lytro unveiled its camera design on Oct...
2005; Georgiev 2006), microscope (Levoy 2006), or other optical system in which an array of microlenses has been inserted in the optical path.
How many images should be in a light field? The largest known light field (of Michelangelo's statue of Night) contains 24,000 1.3-megapixel images. At a deeper level, the answer depends on the application. For light field
rendering (see the Application section below), if you want to walk completely around an opaque object, then of course you need to photograph its back side. Less obviously, if you want to walk close to the object, and the object lies astride the st plane, then you need images taken at finely spaced positions on the uv plane (in the two-plane parameterization shown above), which is now behind you, and these images need to have high spatial resolution.
The number and arrangement of images in a light field, and the resolution of each image, are together called the "sampling" of the 4D light field. Analyses of light field sampling have been undertaken by many researchers; a good starting point is Chai (2000). Also of interest is Durand (2005) for the effects of occlusion, Ramamoorthi (2006) for the effects of lighting and reflection, and Ng
Ren Ng
Dr. Ren Ng is the founder and the chief executive officer of a Mountain View, California-based start-up, Lytro, Inc. . The company is developing light field technology for digital cameras and has received $50 million in venture capital funding..Lytro unveiled its camera design on Oct...
(2005) and Zwicker (2006) for applications to plenoptic camera
Plenoptic camera
A light-field camera, also called a plenoptic camera, is a camera that uses a microlens array to capture 4D light field information about a scene...
s and 3D displays, respectively.
Applications of light fields
Computational imaging refers to any image formation method that involves a digital computer. Many of these methods operate at visiblewavelengths, and many of those produce light fields. As a result, listing all applications of light fields would require surveying all uses of computational imaging in art, science, engineering, and medicine. In computer graphics, some selected applications are:
Illumination engineering. Gershun's reason for studying the light field was to derive (in closed form if possible) the illumination patterns that would be observed on surfaces due to light sources of various shapes positioned above these surface. An example is shown at right. A more modern study is (Ashdown 1993).
Light field rendering. By extracting appropriate 2D slices from the 4D light field of a scene, one can produce novel views of the scene (Levoy 1996; Gortler 1996). Depending on the parameterization of the light field and slices, these views might be perspective, orthographic
Orthographic projection (geometry)
In Euclidean geometry, an orthographic projection is an orthogonal projection. In particular, in 3D it is an affine, parallel projection of an object onto a perpendicular plane....
, crossed-slit (Zomet 2003), multi-perspective (Rademacher 1998), or another type of projection. Light field rendering is one form of image-based rendering
Image-Based Modeling And Rendering
In computer graphics and computer vision, image-based modeling and rendering methods rely on a set of two-dimensional images of a scene to generate a three-dimensional model and then render some novel views of this scene....
.
Synthetic aperture photography. By integrating an appropriate 4D subset of the samples in a light field, one can approximate the view that would be captured by a camera having a finite (i.e. non-pinhole) aperture. Such a view has a finite depth of field
Depth of field
In optics, particularly as it relates to film and photography, depth of field is the distance between the nearest and farthest objects in a scene that appear acceptably sharp in an image...
. By shearing or warping the light field before performing this integration, one can focus on different fronto-parallel (Isaksen 2000) or oblique (Vaish 2005) planes in the scene. If the light field is captured using a handheld camera (Ng
Ren Ng
Dr. Ren Ng is the founder and the chief executive officer of a Mountain View, California-based start-up, Lytro, Inc. . The company is developing light field technology for digital cameras and has received $50 million in venture capital funding..Lytro unveiled its camera design on Oct...
2005), this essentially constitutes a digital camera whose photographs can be refocused after they are taken.
3D display. By presenting a light field using technology that maps each sample to the appropriate ray in physical space, one obtains an
autostereoscopic
Autostereoscopy
Autostereoscopy is any method of displaying stereoscopic images without the use of special headgear or glasses on the part of the viewer. Because headgear is not required, it is also called "glasses-free 3D" or "glassesless 3D"...
visual effect akin to viewing the original scene. Non-digital technologies for doing this include integral photography, parallax panoramagrams
Volumetric display
A volumetric display device is a graphical display device that forms a visual representation of an object in three physical dimensions, as opposed to the planar image of traditional screens that simulate depth through a number of different visual effects...
, and holography
Holography
Holography is a technique that allows the light scattered from an object to be recorded and later reconstructed so that when an imaging system is placed in the reconstructed beam, an image of the object will be seen even when the object is no longer present...
; digital technologies include placing an array of lenslets over a high-resolution display screen, or projecting the imagery onto an array of lenslets using an array of video projectors. If the latter is combined with an array of video cameras, one can capture and display a time-varying light field. This essentially constitutes a 3D television system (Javidi 2002; Matusik 2004).
Image generation and predistortion of synthetic imagery for holographic stereograms is one of the earliest examples of computed light fields, anticipating and later motivating the geometry used in Levoy and Hanrahan's work (Halle 1991, 1994).
Glare reduction. Glare arises due to multiple scattering of light inside the camera’s body and lens optics and reduces image contrast. While glare has been analyzed in 2D image space (Talvala 2007), it is useful to identify it as a 4D ray-space phenomenon (Raskar 2008). By statistically analyzing the ray-space inside a camera, one can classify and remove glare artifacts. In ray-space, glare behaves as high frequency noise and can be reduced by outlier rejection. Such analysis can be performed by capturing the light field inside the camera, but it results in the loss of spatial resolution. Uniform and non-uniform ray sampling could be used to reduce glare without significantly compromising image resolution (Raskar 2008).
Theory
Adelson, E.H., Bergen, J.R. (1991).
"The plenoptic function and the elements of early vision",
In Computation Models of Visual Processing,
M. Landy and J.A. Movshon, eds., MIT Press, Cambridge, 1991, pp. 3–20.
Arvo, J. (1994).
"The Irradiance Jacobian for Partially Occluded Polyhedral Sources",
Proc. ACM SIGGRAPH,
ACM Press, pp. 335–342.
Faraday, M.,
"Thoughts on Ray Vibrations",
Philosophical Magazine,
S.3, Vol XXVIII, N188, May 1846.
Gershun, A. (1936).
"The Light Field",
Moscow, 1936. Translated by P. Moon and G. Timoshenko in
Journal of Mathematics and Physics,
Vol. XVIII, MIT, 1939, pp. 51–151.
Gortler, S.J., Grzeszczuk, R., Szeliski, R., Cohen, M. (1996).
"The Lumigraph",
Proc. ACM SIGGRAPH,
ACM Press, pp. 43–54.
Levoy, M., Hanrahan, P. (1996).
"Light Field Rendering",
Proc. ACM SIGGRAPH,
ACM Press, pp. 31–42.
Moon, P., Spencer, D.E. (1981).
The Photic Field,
MIT Press.
Analysis
Ramamoorthi, R., Mahajan, D., Belhumeur, P. (2006).
"A First Order Analysis of Lighting, Shading, and Shadows",
ACM TOG.
Zwicker, M., Matusik, W., Durand, F., Pfister, H. (2006).
"Antialiasing for Automultiscopic 3D Displays",
Eurographics Symposium on Rendering, 2006.
Ng, R. (2005).
"Fourier Slice Photography",
Proc. ACM SIGGRAPH, ACM Press, pp. 735–744.
Durand, F., Holzschuch, N., Soler, C., Chan, E., Sillion, F. X. (2005).
"A Frequency analysis of Light Transport",
Proc. ACM SIGGRAPH, ACM Press, pp. 1115–1126.
Chai, J.-X., Tong, X., Chan, S.-C., Shum, H. (2000).
"Plenoptic Sampling",
Proc. ACM SIGGRAPH, ACM Press, pp. 307–318.
Halle, M. (1994)
"Holographic stereograms as discrete imaging systems",
in SPIE Proc. Vol. #2176: Practical Holography VIII, S.A. Benton, ed., pp. 73–84.
Devices
Liang, C.K., Lin, T.H., Wong, B.Y., Liu, C., Chen, H. H. (2008).
"Programmable Aperture Photography:Multiplexed Light Field Acquisition", Proc. ACM SIGGRAPH.
Veeraraghavan, A., Raskar, R., Agrawal, A., Mohan, A., Tumblin, J. (2007).
"Dappled Photography: Mask Enhanced Cameras for Heterodyned Light Fields and Coded Aperture Refocusing", Proc. ACM SIGGRAPH.
Georgiev, T., Zheng, C., Nayar, S., Curless, B., Salesin, D., Intwala, C. (2006).
"Spatio-angular Resolution Trade-offs in Integral Photography", Proc. EGSR 2006.
Kanade, T., Saito, H., Vedula, S. (1998).
"The 3D Room: Digitizing Time-Varying 3D Events by Synchronized Multiple Video Streams", Tech report CMU-RI-TR-98-34, December 1998.
Levoy, M. (2002).
Stanford Spherical Gantry.
Levoy, M., Ng, R., Adams, A., Footer, M., Horowitz, M. (2006).
"Light field microscopy",
ACM Transactions on Graphics (Proc. SIGGRAPH),
Vol. 25, No. 3.
Ng, R., Levoy, M., Brédif, M., Duval, G., Horowitz, M., Hanrahan, P. (2005).
"Light Field Photography with a Hand-Held Plenoptic Camera", Stanford Tech Report CTSR 2005-02, April, 2005.
Wilburn, B., Joshi, N., Vaish, V., Talvala, E., Antunez, E., Barth, A., Adams, A., Levoy, M., Horowitz, M. (2005).
"High Performance Imaging Using Large Camera Arrays",
ACM Transactions on Graphics (Proc. SIGGRAPH),
Vol. 24, No. 3, pp. 765–776.
Yang, J.C., Everett, M., Buehler, C., McMillan, L. (2002).
"A real-time distributed light field camera",
Proc. Eurographics Rendering Workshop 2002.
"The CAFADIS camera"
Archives of light fields
"The Stanford Light Field Archive"
"UCSD/MERL Light Field Repository"
Applications
Ashdown, I. (1993).
"Near-Field Photometry: A New Approach",
Journal of the Illuminating Engineering Society,
Vol. 22, No. 1, Winter, 1993, pp. 163–180.
Buehler, C., Bosse, M., McMillan, L., Gortler, S., Cohen, M. (2001).
"Unstructured Lumigraph rendering",
Proc. ACM SIGGRAPH,
ACM Press.
Isaksen, A., McMillan, L., Gortler, S.J. (2000).
"Dynamically Reparameterized Light Fields", Proc. ACM SIGGRAPH, ACM Press, pp. 297–306.
Javidi, B., Okano, F., eds. (2002).
Three-Dimensional Television, Video and Display Technologies,
Springer-Verlag.
Matusik, W., Pfister, H. (2004).
"3D TV: a scalable system for real-time acquisition, transmission, and autostereoscopic display of dynamic scenes",
Proc. ACM SIGGRAPH, ACM Press.
Rademacher, P., Bishop, G. (1998).
"Multiple-Center-of-Projection Images",
Proc. ACM SIGGRAPH,
ACM Press.
Vaish, V., Garg, G., Talvala, E., Antunez, E., Wilburn, B.,
Horowitz, M., Levoy, M. (2005).
"Synthetic Aperture Focusing using a Shear-Warp Factorization of the Viewing Transform",
Proc. Workshop on Advanced 3D Imaging for Safety and Security,
in conjunction with CVPR 2005.
Zomet, A., Feldman, D., Peleg, S., Weinshall, D. (2003).
"Mosaicing new views: the crossed-slits projection",
IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI),
Vol. 25, No. 6, June 2003, pp. 741–754.
Halle, M., Benton, S., Klug, M., Underkoffler, J. (1991).
"The UltraGram: a generalized holographic stereogram",
SPIE Vol. 1461, Practical Holography V, S.A. Benton, ed., pp. 142–155.
Talvala, E-V., Adams, A., Horowitz, M., Levoy, M. (2007).
"Veiling glare in high dynamic range imaging",
Proc. ACM SIGGRAPH.
Raskar, R., Agrawal, A., Wilson, C., Veeraraghavan, A. (2008).
"Glare Aware Photography: 4D Ray Sampling for Reducing Glare Effects of Camera Lenses",
Proc. ACM SIGGRAPH.
Pérez, F., Marichal, J. G., Rodriguez, J.M. (2008).
"The Discrete Focal Stack Transform",
Proc. EUSIPCO

