L-theory
Encyclopedia
Algebraic L-theory is the K-theory
of quadratic form
s; the term was coined by C. T. C. Wall
,
with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',
is important in surgery theory
.
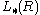(Wall) and the symmetric L-groups 
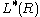(Mishchenko, Ranicki).
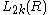are defined as the Witt group
s of ε-quadratic forms over the ring R with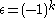
. More precisely,
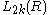
is the abelian group of equivalence classes
of non-degenerate ε-quadratic forms 
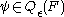over R, where the underlying R-modules F are finitely generated free. The equivalence relation is given by stabilization with respect to hyperbolic ε-quadratic forms:
.
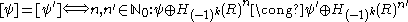The addition in
is defined by
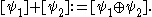
The zero element is represented by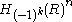
for any 
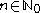. The inverse of 
is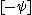 
.
are the L-groups 
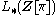of the group ring
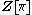. In the applications to topology 
is the fundamental group
of a space 
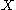. The quadratic L-groups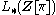 
play a central role in the surgery classification of the homotopy types of
-dimensional manifolds of dimension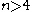 
, and in the formulation of the Novikov conjecture
.
The distinction between symmetric L-groups and quadratic L-groups, indicated by upper and lower indices, reflects the usage in group homology and cohomology. The group cohomology
of the cyclic group 
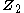deals with the fixed points of a 
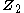-action, while the group homology 
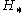deals with the orbits of a 
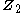-action; compare 
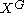(fixed points) and 
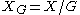(orbits, quotient) for upper/lower index notation.
The quadratic L-groups: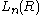
and the symmetric L-groups: 
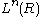are related by
a symmetrization map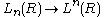
which is an isomorphism modulo 2-torsion, and which corresponds to the polarization identities.
The quadratic L-groups are 4-fold periodic. Symmetric L-groups are not 4-periodic in general (see Ranicki, page 12), though they are for the integers.
In view of the applications to the classification of manifolds
there are extensive calculations of
the quadratic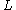
-groups 
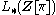. For finite 
algebraic methods are used, and mostly geometric methods (e.g. controlled topology) are used for infinite
.
More generally, one can define L-groups for any additive category
with a chain duality, as in Ranicki (section 1).
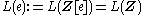for both 
= 
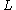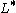or 
For quadratic L-groups, these are the surgery obstructions to simply connected surgery.
The quadratic L-groups of the integers are: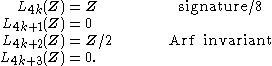
In doubly even dimension (4k), the quadratic L-groups detect the signature
; in singly even dimension (4k+2), the L-groups detect the Arf invariant
.
The symmetric L-groups of the integers are:
In doubly even dimension (4k), the symmetric L-groups, as with the quadratic L-groups, detect the signature; in dimension (4k+1), the L-groups detect the de Rham invariant.
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
of quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s; the term was coined by C. T. C. Wall
C. T. C. Wall
Charles Terence Clegg Wall is a leading British mathematician, educated at Marlborough and Trinity College, Cambridge. He is an emeritus professor of the University of Liverpool, where he was first appointed Professor in 1965...
,
with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',
is important in surgery theory
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
.
Definition
One can define L-groups for any ring with involution R: the quadratic L-groups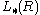 (Wall) and the symmetric L-groups 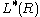(Mishchenko, Ranicki).Even dimension
The even dimensional L-groups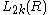 are defined as the Witt groupWitt group
In mathematics, a Witt group of a field, named after Ernst Witt, is an abelian group whose elements are represented by symmetric bilinear forms over the field.-Definition:Fix a field k. All vector spaces will be assumed to be finite-dimensional...
s of ε-quadratic forms over the ring R with
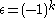. More precisely,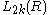is the abelian group of equivalence classes
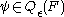of non-degenerate ε-quadratic forms over R, where the underlying R-modules F are finitely generated free. The equivalence relation is given by stabilization with respect to hyperbolic ε-quadratic forms: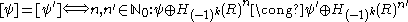.The addition in
is defined by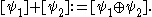The zero element is represented by
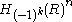for any 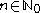. The inverse of is 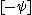.Odd dimension
Defining odd dimensional L-groups is more complicated; further details and the definition of the odd dimensional L-groups can be found in the references mentioned below.Examples and applications
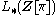The L-groups of a group are the L-groups of the group ringGroup ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
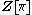. In the applications to topology is the fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
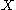of a space . The quadratic L-groups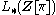 play a central role in the surgery classification of the homotopy types of
-dimensional manifolds of dimension 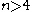, and in the formulation of the Novikov conjectureNovikov conjecture
The Novikov conjecture is one of the most important unsolved problems in topology. It is named for Sergei Novikov who originally posed the conjecture in 1965....
.
The distinction between symmetric L-groups and quadratic L-groups, indicated by upper and lower indices, reflects the usage in group homology and cohomology. The group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
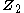of the cyclic group deals with the fixed points of a 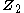-action, while the group homology 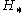deals with the orbits of a 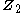-action; compare 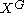(fixed points) and 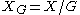(orbits, quotient) for upper/lower index notation.The quadratic L-groups:
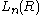and the symmetric L-groups: 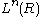are related bya symmetrization map
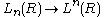which is an isomorphism modulo 2-torsion, and which corresponds to the polarization identities.The quadratic L-groups are 4-fold periodic. Symmetric L-groups are not 4-periodic in general (see Ranicki, page 12), though they are for the integers.
In view of the applications to the classification of manifolds
Classification of manifolds
In mathematics, specifically geometry and topology, the classification of manifolds is a basic question, about which much is known, and many open questions remain.-Overview:...
there are extensive calculations of
the quadratic
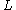-groups 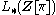. For finite algebraic methods are used, and mostly geometric methods (e.g. controlled topology) are used for infinite
.More generally, one can define L-groups for any additive category
Additive category
In mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
with a chain duality, as in Ranicki (section 1).
Integers
The simply connected L-groups are also the L-groups of the integers, as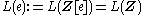 for both 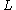= 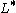or For quadratic L-groups, these are the surgery obstructions to simply connected surgery.The quadratic L-groups of the integers are:
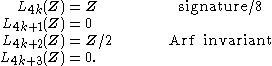
In doubly even dimension (4k), the quadratic L-groups detect the signature
Signature (topology)
In the mathematical field of topology, the signature is an integer invariant which is defined for an oriented manifold M of dimension d=4k divisible by four ....
; in singly even dimension (4k+2), the L-groups detect the Arf invariant
Arf invariant
In mathematics, the Arf invariant of a nonsingular quadratic form over a field of characteristic 2 was defined by when he started the systematic study of quadratic forms over arbitrary fields of characteristic2. The Arf invariant is the substitute, in...
.
The symmetric L-groups of the integers are:
In doubly even dimension (4k), the symmetric L-groups, as with the quadratic L-groups, detect the signature; in dimension (4k+1), the L-groups detect the de Rham invariant.