
Witt group
Encyclopedia
In mathematics, a Witt group of a field, named after Ernst Witt
, is an abelian group
whose elements are represented by symmetric bilinear forms over the field.
s will be assumed to be finite-dimensional. We say that two symmetric bilinear form
s are equivalent if one can be obtained from the other by adding zero or more copies of a hyperbolic plane
(the non-degenerate two-dimensional symmetric bilinear form with a norm 0 vector).
The Witt group of k is the abelian group of equivalence classes of non-degenerate symmetric bilinear forms, with the group operation corresponding to the orthogonal direct sum of forms.
The Witt group of k can be given a commutative ring
structure, by using the tensor product
of two bilinear forms to define the ring product. This is sometimes called the Witt ring of k, though the term "Witt ring" is often also used for a completely different ring of Witt vector
s.
Two number fields K and L are Witt equivalent if and only if there is a bijection T between the places of K and the places of L and a group isomorphism t between their square-class groups, preserving degree 2 Hilbert symbols. In this case the pair (T,t) is called a reciprocity equivalence or a degree 2 Hilbert symbol equivalence. Some variations and extensions of this condition, such as "tame degree l Hilbert symbol equivalence", have also been studied; see the references for details.
s, and more generally ε-quadratic forms, over any *-ring R.
The resulting groups (and generalizations thereof) are known as the even-dimensional symmetric L-group
s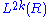 and even-dimensional quadratic L-groups
and even-dimensional quadratic L-groups 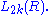 The quadratic L-groups are 4-periodic, with
The quadratic L-groups are 4-periodic, with 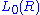 being the Witt group of (1)-quadratic forms (symmetric), and
being the Witt group of (1)-quadratic forms (symmetric), and 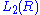 being the Witt group of
being the Witt group of 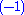 -quadratic forms (skew-symmetric); symmetric L-groups are not 4-periodic for all rings, hence they provide a less exact generalization.
-quadratic forms (skew-symmetric); symmetric L-groups are not 4-periodic for all rings, hence they provide a less exact generalization.
L-groups are central objects in surgery theory
, forming one of the three terms of the surgery exact sequence.
Ernst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
, is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
whose elements are represented by symmetric bilinear forms over the field.
Definition
Fix a field k. All vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s will be assumed to be finite-dimensional. We say that two symmetric bilinear form
Symmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
s are equivalent if one can be obtained from the other by adding zero or more copies of a hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
(the non-degenerate two-dimensional symmetric bilinear form with a norm 0 vector).
The Witt group of k is the abelian group of equivalence classes of non-degenerate symmetric bilinear forms, with the group operation corresponding to the orthogonal direct sum of forms.
The Witt group of k can be given a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
structure, by using the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of two bilinear forms to define the ring product. This is sometimes called the Witt ring of k, though the term "Witt ring" is often also used for a completely different ring of Witt vector
Witt vector
In mathematics, a Witt vector is an infinite sequence of elements of a commutative ring. Ernst Witt showed how to put a ring structure on the set of Witt vectors, in such a way that the ring of Witt vectors over the finite field of order p is the ring of p-adic integers.-Motivation:Any p-adic...
s.
Witt equivalence
Two fields are said to be Witt equivalent if their Witt rings are isomorphic.Two number fields K and L are Witt equivalent if and only if there is a bijection T between the places of K and the places of L and a group isomorphism t between their square-class groups, preserving degree 2 Hilbert symbols. In this case the pair (T,t) is called a reciprocity equivalence or a degree 2 Hilbert symbol equivalence. Some variations and extensions of this condition, such as "tame degree l Hilbert symbol equivalence", have also been studied; see the references for details.
Generalizations
Witt groups can also be defined in the same way for skew-symmetric forms, and for quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s, and more generally ε-quadratic forms, over any *-ring R.
The resulting groups (and generalizations thereof) are known as the even-dimensional symmetric L-group
L-theory
Algebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
s
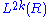 and even-dimensional quadratic L-groups
and even-dimensional quadratic L-groups 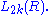 The quadratic L-groups are 4-periodic, with
The quadratic L-groups are 4-periodic, with 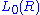 being the Witt group of (1)-quadratic forms (symmetric), and
being the Witt group of (1)-quadratic forms (symmetric), and 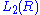 being the Witt group of
being the Witt group of 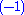 -quadratic forms (skew-symmetric); symmetric L-groups are not 4-periodic for all rings, hence they provide a less exact generalization.
-quadratic forms (skew-symmetric); symmetric L-groups are not 4-periodic for all rings, hence they provide a less exact generalization.L-groups are central objects in surgery theory
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
, forming one of the three terms of the surgery exact sequence.

