
Novikov conjecture
Encyclopedia
The Novikov conjecture is one of the most important unsolved problems in topology
. It is named for Sergei Novikov who originally posed the conjecture in 1965.
The Novikov conjecture concerns the homotopy
invariance of certain polynomial
s in the Pontryagin class
es of a manifold, arising from the fundamental group
. According to the Novikov conjecture, the higher signatures, which are certain numerical invariants of smooth manifolds, are homotopy invariants.
The conjecture has been proved for finitely generated abelian groups. It is not yet known whether the Novikov conjecture holds true for all groups. There are no known counterexamples to the conjecture.
and BG its classifying space
, which is a K(G,1) and therefore unique up to homotopy equivalence as a CW complex. Let

be a continuous map from a closed oriented n-dimensional manifold M to BG, and
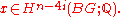
Novikov considered the numerical expression, found by evaluating the cohomology class in top dimension against the fundamental class
[M], and known as the higher signature:
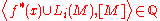
where Li is the ith Hirzebruch polynomial, or sometimes (less descriptively) as the ith L-polynomial. For each i, this polynomial can be expressed in the Pontryagin classes of the manifold's tangent bundle. The Novikov conjecture states that the higher signature is a homotopy invariant for every such map f and every such class x.
in L-theory
. The
Borel conjecture
on the rigidity of aspherical manifolds is equivalent to the assembly map being an isomorphism.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. It is named for Sergei Novikov who originally posed the conjecture in 1965.
The Novikov conjecture concerns the homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
invariance of certain polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in the Pontryagin class
Pontryagin class
In mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
es of a manifold, arising from the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
. According to the Novikov conjecture, the higher signatures, which are certain numerical invariants of smooth manifolds, are homotopy invariants.
The conjecture has been proved for finitely generated abelian groups. It is not yet known whether the Novikov conjecture holds true for all groups. There are no known counterexamples to the conjecture.
Precise formulation of the conjecture
Let G be a discrete groupDiscrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
and BG its classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
, which is a K(G,1) and therefore unique up to homotopy equivalence as a CW complex. Let

be a continuous map from a closed oriented n-dimensional manifold M to BG, and
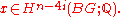
Novikov considered the numerical expression, found by evaluating the cohomology class in top dimension against the fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
[M], and known as the higher signature:
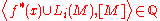
where Li is the ith Hirzebruch polynomial, or sometimes (less descriptively) as the ith L-polynomial. For each i, this polynomial can be expressed in the Pontryagin classes of the manifold's tangent bundle. The Novikov conjecture states that the higher signature is a homotopy invariant for every such map f and every such class x.
Connection with the Borel conjecture
The Novikov conjecture is equivalent to the rational injectivity of the assembly mapAssembly map
In mathematics, assembly maps are an important concept in geometric topology. From the homotopy-theoretical viewpoint, an assembly map is a universal approximation of a homotopy invariant functor by a homology theory from the left...
in L-theory
L-theory
Algebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
. The
Borel conjecture
Borel conjecture
In mathematics, specifically geometric topology, the Borel conjecture asserts that an aspherical closed manifold is determined by its fundamental group, up to homeomorphism...
on the rigidity of aspherical manifolds is equivalent to the assembly map being an isomorphism.
External links
- Biography of Sergei Novikov
- Novikov Conjecture Bibliography
- Novikov Conjecture 1993 Oberwolfach Conference Proceedings, Volume 1
- Novikov Conjecture 1993 Oberwolfach Conference Proceedings, Volume 2
- 2004 Oberwolfach Seminar notes on the Novikov Conjecture (pdf)
- Scholarpedia article by S.P. Novikov (2010)

