
Klein model
Encyclopedia
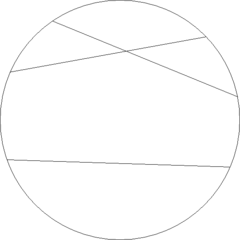


Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
in which points are represented by the points in the interior of the n-dimensional unit ball (or unit disk, in two dimensions) and lines are represented by the chord
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
s, straight line segments with endpoints on the boundary sphere. It made its first appearance in two memoirs of Eugenio Beltrami
Eugenio Beltrami
Eugenio Beltrami was an Italian mathematician notable for his work concerning differential geometry and mathematical physics...
published in 1868, first for n = 2 and then for general n, devoted to showing equiconsistency
Equiconsistency
In mathematical logic, two theories are equiconsistent if, roughly speaking, they are "as consistent as each other".It is not in general possible to prove the absolute consistency of a theory T...
of hyperbolic geometry with ordinary Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
.
The Beltrami–Klein model is strongly analogous to the gnomonic projection
Gnomonic projection
A gnomonic map projection displays all great circles as straight lines. Thus the shortest route between two locations in reality corresponds to that on the map. This is achieved by projecting, with respect to the center of the Earth , the Earth's surface onto a tangent plane. The least distortion...
of spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
, which maps great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s to straight lines; the formulae relating these two to the hyperboloid model
Hyperboloid model
In geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...
and the sphere, respectively, are very similar.
The distance
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
is given by the Cayley–Klein metric
Cayley–Klein metric
In mathematics, a Cayley–Klein metric is a metric on the complement of a fixed quadric in projective space defined using a cross-ratio. The first example was given by , and they were studied further by ....
and was first written down by Arthur Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
in the context of projective
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
and spherical
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
geometry. Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
recognized its importance for non-Euclidean geometry
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
and popularized the subject.
Distance formula
Arthur CayleyArthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
applied the cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
from projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
to measurement of distances and angles in spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
. Later, Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
realized that Cayley's ideas give rise to a projective model of the non-Euclidean plane.
Given two distinct points p and q in the open unit ball, the unique straight line connecting them intersects the unit sphere in two points, a and b, labeled so that the points are, in order, a, p, q, b. Then the hyperbolic distance between p and q is expressed as
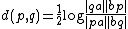
where the vertical bars indicate Euclidean distances. The factor of one half is need to make the curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
−1.
Relation to the hyperboloid model
The hyperboloid modelHyperboloid model
In geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...
is a model of hyperbolic geometry within (n + 1)-dimensional Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. The Minkowski inner product is given by
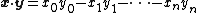
and the norm by
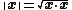 . The hyperbolic plane is embedded in this space as the vectors x with ||x|| = 1 and x0 (the "timelike component") positive. The intrinsic distance (in the embedding) between points u and v is then given by
. The hyperbolic plane is embedded in this space as the vectors x with ||x|| = 1 and x0 (the "timelike component") positive. The intrinsic distance (in the embedding) between points u and v is then given by
This may also be written in the homogeneous form
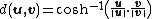
which allows the vectors to be rescaled for convenience.
The Beltrami–Klein model is obtained from the hyperboloid model by rescaling all vectors so that the timelike component is 1, that is, by projecting the hyperboloid embedding through the origin onto the plane x0 = 1. This maps the hyperbolic plane into a ball of radius 1, with the spherical boundary of the ball corresponding to the conformal infinity of the hyperbolic plane. The distance function, in its homogeneous form, is unchanged. Since the intrinsic lines (geodesics) of the hyperboloid model are the intersection of the embedding with planes through the Minkowski origin, the intrinsic lines of the Beltrami–Klein model are the chords of the sphere.
In the gyrovector space
Gyrovector space
A gyrovector space is a mathematical concept for studying hyperbolic geometry in analogy to the way vector spaces are used in Euclidean geometry. This vector-based approach has been developed by Abraham Albert Ungar from the late 1980s onwards...
approach to hyperbolic geometry, vector algebra in the Beltrami–Klein model can be developed using relativistic 3-velocities
Velocity-addition formula
In physics, a velocity-addition formula is an equation that relates the velocities of moving objects in different reference frames.- Galilean addition of velocities :...
as the vectors, analogously to the use of ordinary vectors in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
.
Relation to the Poincaré disk model
Both the Poincaré disk modelPoincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
and the Beltrami–Klein model are models of the n-dimensional hyperbolic space in the n-dimensional unit ball in Rn. If
 is a vector of norm less than one representing a point of the Poincaré disk model, then the corresponding point of the Beltrami–Klein model is given by
is a vector of norm less than one representing a point of the Poincaré disk model, then the corresponding point of the Beltrami–Klein model is given by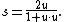
Conversely, from a vector
 of norm less than one representing a point of the Beltrami–Klein model, the corresponding point of the Poincaré disk model is given by
of norm less than one representing a point of the Beltrami–Klein model, the corresponding point of the Poincaré disk model is given by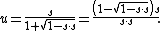
Given two points on the boundary of the unit disk, which are traditionally called ideal points, the straight line connecting them in the Beltrami–Klein model is the chord between them, while in the corresponding Poincaré model the line is a circular arc on the two-dimensional subspace generated by the two boundary point vectors, orthogonal to the boundary of the disk. The two models are related through a projection from the center of the disk; a ray from the center passing through a point of one model line passes through the corresponding point of the line in the other model.

