
Universal set
Encyclopedia
In set theory
, a universal set is a set which contains all objects, including itself. In set theory
as usually formulated, the conception of a set of all sets leads to a paradox
. The reason for this lies with Zermelo's axiom of comprehension: for any
formula and set A, the set
and set A, the set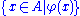
which contains exactly those elements x of A that satisfy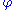 exists. If the
exists. If the
universal set V existed and the axiom of separation applied to it, then Russell's paradox
would arise from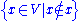 .
.
More generally, for any set A we can prove that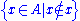
is not an element of A.
A second issue is that the power set of the set of all sets would be a subset of the set of all sets, providing that both exist. This conflicts with Cantor's theorem that the power set of any set (whether infinite or not) always has strictly higher cardinality than the set itself.
The idea of a universal set seems intuitively desirable in the Zermelo–Fraenkel set theory
, particularly because most versions of this theory do allow the use of quantifiers over all sets (see universal quantifier). This is handled by allowing carefully circumscribed
mention of V and similar large collections as proper classes
. In theories in which the universe is a
proper class, is not true because proper classes cannot
is not true because proper classes cannot
be elements.
the universal set V does exist (and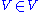 is true). In these theories,
is true). In these theories,
Zermelo's axiom of separation does not hold in general, and the axiom of comprehension
of naive set theory
is restricted in a different way.
The most widely studied set theory with a universal set is Willard Van Orman Quine
’s New Foundations
. Alonzo Church
and Arnold Oberschelp also published work on such set theories. Church speculated that his theory might be extended in a manner consistent with Quine’s, but this is not possible for Oberschelp’s, since in it the singleton function is provably a set, which leads immediately to paradox in New Foundations.
Zermelo–Fraenkel set theory
and related set theories, which are based on the idea of the cumulative hierarchy, do not allow for the existence of a universal set.
and random variables, the universal set or sample space is the one that contains all possible events.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a universal set is a set which contains all objects, including itself. In set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
as usually formulated, the conception of a set of all sets leads to a paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
. The reason for this lies with Zermelo's axiom of comprehension: for any
formula
 and set A, the set
and set A, the set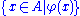
which contains exactly those elements x of A that satisfy
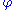 exists. If the
exists. If theuniversal set V existed and the axiom of separation applied to it, then Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
would arise from
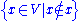 .
.More generally, for any set A we can prove that
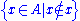
is not an element of A.
A second issue is that the power set of the set of all sets would be a subset of the set of all sets, providing that both exist. This conflicts with Cantor's theorem that the power set of any set (whether infinite or not) always has strictly higher cardinality than the set itself.
The idea of a universal set seems intuitively desirable in the Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, particularly because most versions of this theory do allow the use of quantifiers over all sets (see universal quantifier). This is handled by allowing carefully circumscribed
mention of V and similar large collections as proper classes
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
. In theories in which the universe is a
proper class,
 is not true because proper classes cannot
is not true because proper classes cannotbe elements.
Set theories with a universal set
There are set theories known to be consistent (if the usual set theory is consistent) in whichthe universal set V does exist (and
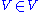 is true). In these theories,
is true). In these theories,Zermelo's axiom of separation does not hold in general, and the axiom of comprehension
of naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
is restricted in a different way.
The most widely studied set theory with a universal set is Willard Van Orman Quine
Willard Van Orman Quine
Willard Van Orman Quine was an American philosopher and logician in the analytic tradition...
’s New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
. Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
and Arnold Oberschelp also published work on such set theories. Church speculated that his theory might be extended in a manner consistent with Quine’s, but this is not possible for Oberschelp’s, since in it the singleton function is provably a set, which leads immediately to paradox in New Foundations.
Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
and related set theories, which are based on the idea of the cumulative hierarchy, do not allow for the existence of a universal set.
Uses in other areas of mathematics
In probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and random variables, the universal set or sample space is the one that contains all possible events.
See also
- Category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
- Non-well-founded set theoryNon-well-founded set theoryNon-well-founded set theories are variants of axiomatic set theory which allow sets to contain themselves and otherwise violate the rule of well-foundedness...
- Russell's paradoxRussell's paradoxIn the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
- UniverseUniverse (mathematics)In mathematics, and particularly in set theory and the foundations of mathematics, a universe is a class that contains all the entities one wishes to consider in a given situation...

