Hydrogen molecular ion
Encyclopedia
The hydrogen molecular ion, dihydrogen cation, or H2+, is the simplest molecular ion. It is composed of two positively-charged proton
s and one negatively-charged electron
, and can be formed from ionization
of a neutral hydrogen molecule. It is of great historical and theoretical interest because, having only one electron, the Schrödinger equation
for the system can be solved in a relatively straightforward way due to the lack of electron–electron repulsion (electron correlation). The analytical solutions for the energy eigenvalues are a generalization of the Lambert W function (see Lambert W function and references therein for more details on this function). Thus, the case of clamped nuclei can be completely done analytically using a Computer algebra system
. Consequently, it is included as an example in most quantum chemistry
textbooks.
The first successful quantum mechanical treatment of H2+ was published by the Danish physicist Øyvind Burrau in 1927, just one year after the publication of wave mechanics by Erwin Schrödinger
. Earlier attempts using the old quantum theory
had been published in 1922 by Karel Niessen
and Wolfgang Pauli
, and in 1925 by Harold Urey
. In 1928, Linus Pauling
published a review putting together the work of Burrau with the work of Walter Heitler
and Fritz London
on the hydrogen molecule.
Bonding in H2+ can be described as a covalent one-electron bond, which has a formal bond order
of one half.
The ion is commonly formed in molecular cloud
s in space, and is important in the chemistry of the interstellar medium
.
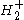is modeled with two fixed nuclear centers, labeled A and B, and one electron. It can be written as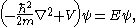
where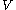
is the electron-nuclear Coulomb potential energy function: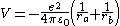
and E is the (electronic) energy of a given quantum mechanical state (eigenstate), with the electronic state function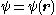
depending on the spatial coordinates of the electron. An additive term 
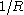, which is constant for fixed inter-nuclear distance 
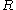, has been omitted from the potential 
, since it merely shifts the eigenvalue. The distances between the electron and the nuclei are denoted 
and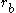 
. In atomic units 
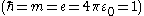the wave equation is
We can choose the midpoint between the nuclei as the origin of coordinates. It follows from general symmetry principles that the wave functions can be characterized by their symmetry behavior with respect to space inversion (r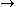
-r). There are wave functions :
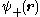, which are symmetric with respect to space inversion, and there are wave functions :
, which are anti-symmetric under this symmetry operation: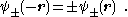 
We note that the permutation (exchange) of the nuclei has a similar effect on the electronic wave function. We only mention that for a many-electron system proper behavior of 
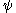with respect to the permutational symmetry of the electrons (Pauli exclusion principle
) must be guaranteed, in addition to those symmetries just discussed above. Now the Schrödinger equations for these symmetry-adapted wave functions are
The ground state (the lowest discrete state) of
is the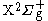 
state with the corresponding wave function 
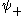denoted as 
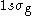. There is also the first excited 
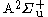state, with its 
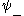labeled as 
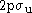. (The suffixes g and u
are from the German gerade and ungerade) occurring here denote just the symmetry behavior under space inversion. Their use is standard practice for the designation of electronic states of diatomic molecules, whereas for atomic states the terms even and odd are used. Asymptotically, the (total) eigenenergies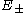
for these two lowest lying states have the same asymptotic expansion in inverse powers of the inter-nuclear distance R :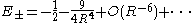
The actual difference between these two energies is called the exchange energy
splitting and is given by :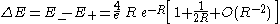
which exponentially vanishes as the inter-nuclear distance R gets greater. The lead term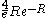
was first obtained by the Holstein–Herring method. Similarly, asympotic expansions in powers of 1/R have been obtained to high order by Cizek et al. for the lowest ten discrete states of the hydrogen molecular ion (clamped nuclei case). For general diatomic and polyatomic molecular systems, the exchange energy is thus very elusive to calculate at large inter-nuclear distances but is nonetheless needed for long-range interactions including studies related to magnetism and charge exchange effects. These are of particular importance in stellar and atmospheric physics.
The energies for the lowest discrete states are shown in the graph above. These can be obtained to within arbitrary accuracy using computer algebra from the generalized Lambert W function (see eq.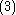
in that site and the reference of Scott, Aubert-Frécon, and Grotendorst) but were obtained initially by numerical means to within double precision by the most precise program available, namely ODKIL. The red full lines are 
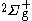states. The green dashed lines are 
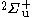states. The blue dashed line is a 
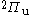state and the pink dotted line is a 
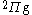state. Note that although the generalized Lambert W function eigenvalue solutions supersede these asymptotic expansions, in practice, they are most useful near the bond length
. These solutions are possible because the partial differential equation
of the wave equation here separates into two coupled ordinary differential equations using prolate spheroidal coordinates
.
s and the hydrogen molecule. An electron is knocked off leaving the cation behind.
Cosmic ray particles have enough energy to ionize many molecules before coming to a stop.
In nature the ion is destroyed by reacting with other hydrogen molecules:
The ionization energy of the hydrogen molecule is 15.603 eV. The dissociation energy of the ion is 1.8 eV. High speed electrons also cause ionization of hydrogen molecules. The peak cross section for ionization for high speed protons is 70000 eV with a cross section of 2.5x10−16 cm2. A cosmic ray proton at lower energy can also strip an electron off a neutral hydrogen molecule to form a neutral hydrogen atom, with a peak cross section at around 8000 eV of 8x10−16 cm2.
An artificial plasma discharge cell can also produce the ion.
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s and one negatively-charged electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, and can be formed from ionization
Ionization
Ionization is the process of converting an atom or molecule into an ion by adding or removing charged particles such as electrons or other ions. This is often confused with dissociation. A substance may dissociate without necessarily producing ions. As an example, the molecules of table sugar...
of a neutral hydrogen molecule. It is of great historical and theoretical interest because, having only one electron, the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for the system can be solved in a relatively straightforward way due to the lack of electron–electron repulsion (electron correlation). The analytical solutions for the energy eigenvalues are a generalization of the Lambert W function (see Lambert W function and references therein for more details on this function). Thus, the case of clamped nuclei can be completely done analytically using a Computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
. Consequently, it is included as an example in most quantum chemistry
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
textbooks.
The first successful quantum mechanical treatment of H2+ was published by the Danish physicist Øyvind Burrau in 1927, just one year after the publication of wave mechanics by Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
. Earlier attempts using the old quantum theory
Old quantum theory
The old quantum theory was a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was a collection of heuristic prescriptions which are now understood to be the first quantum corrections to classical mechanics...
had been published in 1922 by Karel Niessen
Karel Niessen
Karel Frederik Niessen was a Dutch theoretical physicist who made contributions to quantum mechanics and is known for the Pauli-Niessen model.-Education:...
and Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
, and in 1925 by Harold Urey
Harold Urey
Harold Clayton Urey was an American physical chemist whose pioneering work on isotopes earned him the Nobel Prize in Chemistry in 1934...
. In 1928, Linus Pauling
Linus Pauling
Linus Carl Pauling was an American chemist, biochemist, peace activist, author, and educator. He was one of the most influential chemists in history and ranks among the most important scientists of the 20th century...
published a review putting together the work of Burrau with the work of Walter Heitler
Walter Heitler
Walter Heinrich Heitler was a German physicist who made contributions to quantum electrodynamics and quantum field theory...
and Fritz London
Fritz London
Fritz Wolfgang London was a German theoretical physicist. His fundamental contributions to the theories of chemical bonding and of intermolecular forces are today considered classic and are discussed in standard textbooks of physical chemistry.With his brother Heinz, he made a significant...
on the hydrogen molecule.
Bonding in H2+ can be described as a covalent one-electron bond, which has a formal bond order
Bond order
Bond order is the number of chemical bonds between a pair of atoms. For example, in diatomic nitrogen N≡N the bond order is 3, while in acetylene H−C≡C−H the bond order between the two carbon atoms is also 3, and the C−H bond order is 1. Bond order gives an indication to the stability of a bond....
of one half.
The ion is commonly formed in molecular cloud
Molecular cloud
A molecular cloud, sometimes called a stellar nursery if star formation is occurring within, is a type of interstellar cloud whose density and size permits the formation of molecules, most commonly molecular hydrogen ....
s in space, and is important in the chemistry of the interstellar medium
Interstellar medium
In astronomy, the interstellar medium is the matter that exists in the space between the star systems in a galaxy. This matter includes gas in ionic, atomic, and molecular form, dust, and cosmic rays. It fills interstellar space and blends smoothly into the surrounding intergalactic space...
.
Quantum mechanical treatment, symmetries, and asymptotics
The simplest electronic Schrödinger wave equation for the hydrogen molecular ion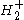 is modeled with two fixed nuclear centers, labeled A and B, and one electron. It can be written as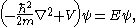where
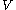is the electron-nuclear Coulomb potential energy function: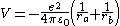and E is the (electronic) energy of a given quantum mechanical state (eigenstate), with the electronic state function
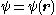depending on the spatial coordinates of the electron. An additive term 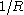, which is constant for fixed inter-nuclear distance 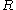, has been omitted from the potential , since it merely shifts the eigenvalue. The distances between the electron and the nuclei are denoted and 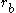. In atomic units 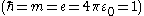the wave equation isWe can choose the midpoint between the nuclei as the origin of coordinates. It follows from general symmetry principles that the wave functions can be characterized by their symmetry behavior with respect to space inversion (r
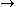-r). There are wave functions :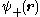, which are symmetric with respect to space inversion, and there are wave functions :, which are anti-symmetric under this symmetry operation: 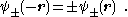We note that the permutation (exchange) of the nuclei has a similar effect on the electronic wave function. We only mention that for a many-electron system proper behavior of 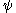with respect to the permutational symmetry of the electrons (Pauli exclusion principlePauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
) must be guaranteed, in addition to those symmetries just discussed above. Now the Schrödinger equations for these symmetry-adapted wave functions are
The ground state (the lowest discrete state) of
is the 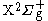state with the corresponding wave function 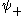denoted as 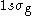. There is also the first excited 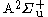state, with its 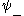labeled as 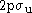. (The suffixes g and uMolecular term symbol
In molecular physics, the molecular term symbol is a shorthand expression of the group representation and angular momenta that characterize the state of a molecule, i.e. its electronic quantum state which is an eigenstate of the electronic molecular Hamiltonian. It is the equivalent of the term...
are from the German gerade and ungerade) occurring here denote just the symmetry behavior under space inversion. Their use is standard practice for the designation of electronic states of diatomic molecules, whereas for atomic states the terms even and odd are used. Asymptotically, the (total) eigenenergies
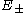for these two lowest lying states have the same asymptotic expansion in inverse powers of the inter-nuclear distance R :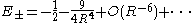The actual difference between these two energies is called the exchange energy
Exchange interaction
In physics, the exchange interaction is a quantum mechanical effect without classical analog which increases or decreases the expectation value of the energy or distance between two or more identical particles when their wave functions overlap...
splitting and is given by :
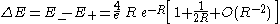
which exponentially vanishes as the inter-nuclear distance R gets greater. The lead term
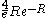was first obtained by the Holstein–Herring method. Similarly, asympotic expansions in powers of 1/R have been obtained to high order by Cizek et al. for the lowest ten discrete states of the hydrogen molecular ion (clamped nuclei case). For general diatomic and polyatomic molecular systems, the exchange energy is thus very elusive to calculate at large inter-nuclear distances but is nonetheless needed for long-range interactions including studies related to magnetism and charge exchange effects. These are of particular importance in stellar and atmospheric physics.The energies for the lowest discrete states are shown in the graph above. These can be obtained to within arbitrary accuracy using computer algebra from the generalized Lambert W function (see eq.
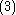in that site and the reference of Scott, Aubert-Frécon, and Grotendorst) but were obtained initially by numerical means to within double precision by the most precise program available, namely ODKIL. The red full lines are 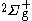states. The green dashed lines are 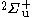states. The blue dashed line is a 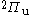state and the pink dotted line is a 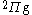state. Note that although the generalized Lambert W function eigenvalue solutions supersede these asymptotic expansions, in practice, they are most useful near the bond lengthBond length
- Explanation :Bond length is related to bond order, when more electrons participate in bond formation the bond will get shorter. Bond length is also inversely related to bond strength and the bond dissociation energy, as a stronger bond will be shorter...
. These solutions are possible because the partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
of the wave equation here separates into two coupled ordinary differential equations using prolate spheroidal coordinates
Prolate spheroidal coordinates
Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating a spheroid around its major axis, i.e., the axis on which the foci are located...
.
Formation
The dihydrogen ion is formed in nature by the interaction of cosmic rayCosmic ray
Cosmic rays are energetic charged subatomic particles, originating from outer space. They may produce secondary particles that penetrate the Earth's atmosphere and surface. The term ray is historical as cosmic rays were thought to be electromagnetic radiation...
s and the hydrogen molecule. An electron is knocked off leaving the cation behind.
- H2 + cosmic ray → H2+ + e- + cosmic ray.
Cosmic ray particles have enough energy to ionize many molecules before coming to a stop.
In nature the ion is destroyed by reacting with other hydrogen molecules:
- H2+ + H2 → H3+ + H.
The ionization energy of the hydrogen molecule is 15.603 eV. The dissociation energy of the ion is 1.8 eV. High speed electrons also cause ionization of hydrogen molecules. The peak cross section for ionization for high speed protons is 70000 eV with a cross section of 2.5x10−16 cm2. A cosmic ray proton at lower energy can also strip an electron off a neutral hydrogen molecule to form a neutral hydrogen atom, with a peak cross section at around 8000 eV of 8x10−16 cm2.
An artificial plasma discharge cell can also produce the ion.
See also
- Dirac Delta function model ( 1-D version of H2+)
- Di-positroniumDi-positroniumDi-positronium, or dipositronium, is a molecule consisting of two atoms of positronium. It was predicted to exist in 1946 by John Archibald Wheeler, and subsequently studied theoretically, but was not observed until 2007 in an experiment done by David Cassidy and Allen Mills at the University of...
- Euler's three-body problemEuler's three-body problemIn physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass...
(classical counterpart) - Few-body systemsFew-body systemsIn quantum mechanics and classical mechanics, a few-body system consists of a small number of well-defined structures or point particles.In quantum mechanics, examples of few-body systems include light nuclear systems , small molecules, light atoms , atomic collisions, and quantum...
- Trihydrogen cation
- Lambert W function
- Molecular astrophysicsAtomic and Molecular astrophysicsAtomic astrophysics is concerned with performing atomic physics calculations that will be useful to astronomers and using atomic data to interpret astronomical observations...
- Holstein–Herring method
- Three-body problemThree-body problemThree-body problem has two distinguishable meanings in physics and classical mechanics:# In its traditional sense the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then...