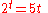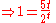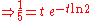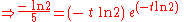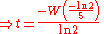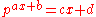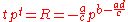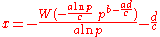
Lambert W function
Encyclopedia
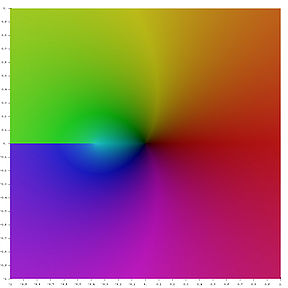
In mathematics
, the Lambert W function, also called the Omega function or product logarithm, is a set of functions
,
namely the branches of the inverse relation
of the function f(w) = wew where ew is the exponential function
and w is any complex number. In other words, the defining equation for W(z) is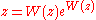
for any complex number z.
Since the function ƒ is not injective, the relation W is multivalued
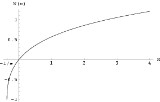
(except at 0). If we restrict attention to real-valued W then the relation is defined only for x ≥ −1/e, and is double-valued on (−1/e, 0); the additional constraint W ≥ −1 defines a single-valued function W0(x). We have W0(0) = 0 and W0(−1/e) = −1. Meanwhile, the lower branch has W ≤ −1 and is denoted W−1(x). It decreases from W−1(−1/e) = −1 to W−1(0−) = −∞.
The Lambert W relation cannot be expressed in terms of elementary functions. It is useful in combinatorics
, for instance in the enumeration of trees. It can be used to solve various equations involving exponentials (e.g. the maxima of the Planck, Bose-Einstein, and Fermi-Dirac distributions) and also occurs in the solution of delay differential equation
s, such as y(t) = a y(t − 1).
. The main branch W0 is denoted by Wp in the Digital Library of Mathematical Functions
and the branch W−1 is denoted by Wm there.
The notation convention chosen here (with W0 and W−1) follows the canonical reference on the Lambert-W function by Corless, Gonnet, Hare, Jeffrey and Knuth
.
in 1783 that discussed the special case of wew. However the inverse of wew was first described by Pólya and Szegő in 1925. The Lambert W function was "re-discovered" every decade or so in specialized applications but its full importance was not realized until the 1990s. When it was reported that the Lambert W function provides an exact solution to the quantum-mechanical double-well Dirac delta function model for equal charges—a fundamental problem in Physics—Corless and developers of the Maple Computer algebra system made a library search to find that this function was in fact ubiquitous to nature.
(W is not differentiable for z=−1/e.) As a consequence, we get the following formula for the derivative of W:
Furthermore we have
using the substitution w = W(x), i.e. x = w ew:
of
around 0 can be found using the Lagrange inversion theorem
and is given by
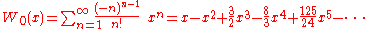
The radius of convergence
is 1/e, as may be seen by the ratio test. The function defined by this series can be extended to a holomorphic function
defined on all complex numbers with a branch cut along the interval
(−∞, −1/e] ; this holomorphic function defines the principal branch
of the Lambert W function.
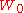also admit simple Taylor (or Laurent
) series expansions at
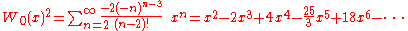
More generally, for
, the Lagrange inversion formula gives
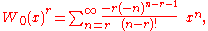
which is, in general, a Laurent series of order r. Equivalently, the latter can be written in the form of a Taylor expansion of powers of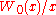
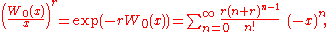
which holds for any
and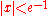 
.
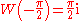
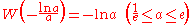
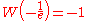
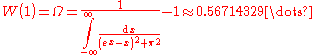(the Omega constant)
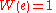
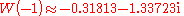
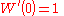
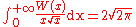
s involving exponentials can be solved using the W function. The general strategy is to move all instances of the unknown to one side of the equation and make it look like Y = XeX at which point the W function provides the value of the variable in X.
In other words :
More generally, the equation
where
can be transformed via the substitution
into
giving
which yields the final solution
Example 2
Similar techniques show that
has solution
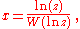
or, equivalently,
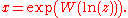
Example 3
Whenever the complex infinite exponential tetration
converges, the Lambert W function provides the actual limit value as
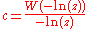
where ln(z) denotes the principal branch of the complex log function.
Example 4
Solutions for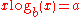
have the form
Example 5
The solution for the current
in a series diode
/resistor
circuit
can also be written in terms of the Lambert W. See diode modeling.
Example 6
The delay differential equation
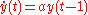
has characteristic equation
, leading to 
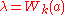and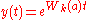 
, where 
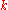is the branch index. If 
is real, only 
need be considered.
Example 7
Granular and debris flow fronts and deposits, and the fronts of viscous fluids in natural events and in the laboratory experiments can be described by using the Lambert–Euler omega function as follows: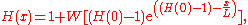
where H(x) is the debris flow height, x is the channel downstream position, L is the unified model parameter consisting of several physical and geometrical parameters of the flow, flow height and the hydraulic pressure gradient.
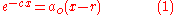
where a0, c and r are real constants. The solution is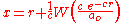
. Generalizations of the Lambert W function include:
Applications of the Lambert "W" function in fundamental physical problems are not exhausted even for the standard case expressed in (1) as seen recently in the area of atomic, molecular, and optical physics
.
,
with successive approximations to
(so 
) being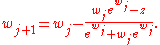
The W function may also be approximated using Halley's method
,
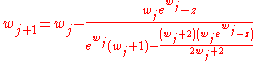
given in Corless et al. to compute W.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lambert W function, also called the Omega function or product logarithm, is a set of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
,
namely the branches of the inverse relation
Inverse relation
In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
of the function f(w) = wew where ew is the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
and w is any complex number. In other words, the defining equation for W(z) is
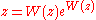
for any complex number z.
Since the function ƒ is not injective, the relation W is multivalued
Multivalued function
In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
(except at 0). If we restrict attention to real-valued W then the relation is defined only for x ≥ −1/e, and is double-valued on (−1/e, 0); the additional constraint W ≥ −1 defines a single-valued function W0(x). We have W0(0) = 0 and W0(−1/e) = −1. Meanwhile, the lower branch has W ≤ −1 and is denoted W−1(x). It decreases from W−1(−1/e) = −1 to W−1(0−) = −∞.
The Lambert W relation cannot be expressed in terms of elementary functions. It is useful in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, for instance in the enumeration of trees. It can be used to solve various equations involving exponentials (e.g. the maxima of the Planck, Bose-Einstein, and Fermi-Dirac distributions) and also occurs in the solution of delay differential equation
Delay differential equation
In mathematics, delay differential equations are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times....
s, such as y(t) = a y(t − 1).
Terminology
The Lambert W-function is named after Johann Heinrich LambertJohann Heinrich Lambert
Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
. The main branch W0 is denoted by Wp in the Digital Library of Mathematical Functions
Digital Library of Mathematical Functions
The Digital Library of Mathematical Functions is an online project at the National Institute of Standards and Technology to develop a major resource of mathematical reference data for special functions and their applications. It is intended as an update of Abramowitz's and Stegun's Handbook of...
and the branch W−1 is denoted by Wm there.
The notation convention chosen here (with W0 and W−1) follows the canonical reference on the Lambert-W function by Corless, Gonnet, Hare, Jeffrey and Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
.
History
Lambert first considered the related Lambert's Transcendental Equation in 1758, which led to a paper by Leonhard EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
in 1783 that discussed the special case of wew. However the inverse of wew was first described by Pólya and Szegő in 1925. The Lambert W function was "re-discovered" every decade or so in specialized applications but its full importance was not realized until the 1990s. When it was reported that the Lambert W function provides an exact solution to the quantum-mechanical double-well Dirac delta function model for equal charges—a fundamental problem in Physics—Corless and developers of the Maple Computer algebra system made a library search to find that this function was in fact ubiquitous to nature.
Derivative
By implicit differentiation, one can show that all branches of W satisfy the differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
(W is not differentiable for z=−1/e.) As a consequence, we get the following formula for the derivative of W:
Furthermore we have
Antiderivative
The function W(x), and many expressions involving W(x), can be integratedIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
using the substitution w = W(x), i.e. x = w ew:
Taylor series
The Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of
around 0 can be found using the Lagrange inversion theoremLagrange inversion theorem
In mathematical analysis, the Lagrange inversion theorem, also known as the Lagrange-Bürmann formula, gives the Taylor series expansion of the inverse function of an analytic function.-Theorem statement:...
and is given by
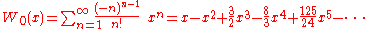
The radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
is 1/e, as may be seen by the ratio test. The function defined by this series can be extended to a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
defined on all complex numbers with a branch cut along the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
(−∞, −1/e
Principal branch
In mathematics, a principal branch is a function which selects one branch, or "slice", of a multi-valued function. Most often, this applies to functions defined on the complex plane: see branch cut....
of the Lambert W function.
Integer and complex powers
Integer powers of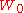 also admit simple Taylor (or LaurentLaurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
) series expansions at
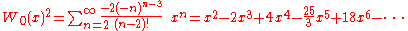
More generally, for
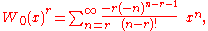
, the Lagrange inversion formula giveswhich is, in general, a Laurent series of order r. Equivalently, the latter can be written in the form of a Taylor expansion of powers of
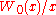
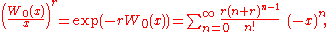
which holds for any
and 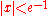.Special values
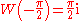
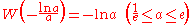
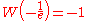
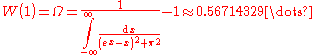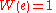
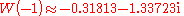
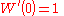
(the Omega constant)Other formulas
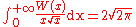
Applications
Many equationEquation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s involving exponentials can be solved using the W function. The general strategy is to move all instances of the unknown to one side of the equation and make it look like Y = XeX at which point the W function provides the value of the variable in X.
In other words :
Examples
Example 1
More generally, the equation
where
can be transformed via the substitution
into
giving
which yields the final solution
Example 2
Similar techniques show that
has solution
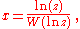
or, equivalently,
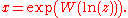
Example 3
Whenever the complex infinite exponential tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
converges, the Lambert W function provides the actual limit value as
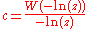
where ln(z) denotes the principal branch of the complex log function.
Example 4
Solutions for
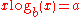
have the form
Example 5
The solution for the current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
in a series diode
Diode
In electronics, a diode is a type of two-terminal electronic component with a nonlinear current–voltage characteristic. A semiconductor diode, the most common type today, is a crystalline piece of semiconductor material connected to two electrical terminals...
/resistor
Resistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
circuit
Electrical network
An electrical network is an interconnection of electrical elements such as resistors, inductors, capacitors, transmission lines, voltage sources, current sources and switches. An electrical circuit is a special type of network, one that has a closed loop giving a return path for the current...
can also be written in terms of the Lambert W. See diode modeling.
Example 6
The delay differential equation
Delay differential equation
In mathematics, delay differential equations are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times....
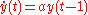
has characteristic equation
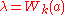, leading to and 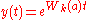, where 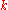is the branch index. If is real, only need be considered.Example 7
Granular and debris flow fronts and deposits, and the fronts of viscous fluids in natural events and in the laboratory experiments can be described by using the Lambert–Euler omega function as follows:
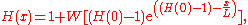
where H(x) is the debris flow height, x is the channel downstream position, L is the unified model parameter consisting of several physical and geometrical parameters of the flow, flow height and the hydraulic pressure gradient.
Generalizations
The standard Lambert W function expresses exact solutions to transcendental algebraic equations (in x) of the form: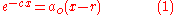where a0, c and r are real constants. The solution is
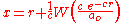. Generalizations of the Lambert W function include:
- An application to general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
and quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
(quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
) in lower dimensions, in fact a previously unknown link between these two areas, as shown in Classical and Quantum GravityClassical and Quantum GravityClassical and Quantum Gravity is a peer-reviewed journal that covers all aspects of gravitational physics and the theory of spacetime.Its scope includes*Classical general relativity*Applications of relativity*Experimental gravitation...
where the right-hand-side of (1) is now a quadratic polynomial in x:
- and where r1 and r2 are real distinct constants, the roots of the quadratic polynomial. Here, the solution is a function has a single argument x but the terms like ri and ao are parameters of that function. In this respect, the generalization resembles the hypergeometric function and the Meijer G-functionMeijer G-FunctionIn mathematics, the G-function was introduced by as a very general function intended to include most of the known special functions as particular cases. This was not the only attempt of its kind: the generalized hypergeometric function and the MacRobert E-function had the same aim, but Meijer's...
but it belongs to a different class of functions. When r1 = r2, both sides of (2) can be factored and reduced to (1) and thus the solution reduces to that of the standard W function. Eq. (2) expresses the equation governing the dilatonDilatonIn particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
field, from which is derived the metric of the R=T or lineal two-body gravity problem in 1+1 dimensions (one spatial dimension and one time dimension) for the case of unequal (rest) masses, as well as, the eigenenergies of the quantum-mechanical double-well Dirac delta function model for unequal charges in one dimension.- Analytical solutions of the eigenenergies of a special case of the quantum mechanical three-body problemEuler's three-body problemIn physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass...
, namely the (three-dimensional) hydrogen molecule-ion. Here the right-hand-side of (1) (or (2)) is now a ratio of infinite order polynomials in x:
- Analytical solutions of the eigenenergies of a special case of the quantum mechanical three-body problem
- where ri and si are distinct real constants and x is a function of the eigenenergy and the internuclear distance R. Eq. (3) with its specialized cases expressed in (1) and (2) is related to a large class of delay differential equationDelay differential equationIn mathematics, delay differential equations are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times....
s.
Applications of the Lambert "W" function in fundamental physical problems are not exhausted even for the standard case expressed in (1) as seen recently in the area of atomic, molecular, and optical physics
Atomic, molecular, and optical physics
Atomic, molecular, and optical physics is the study of matter-matter and light-matter interactions on the scale of single atoms or structures containing a few atoms. The three areas are grouped together because of their interrelationships, the similarity of methods used, and the commonality of the...
.
Numerical evaluation
The W function may be approximated using Newton's methodNewton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
,
with successive approximations to
(so ) being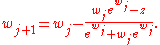The W function may also be approximated using Halley's method
Halley's method
In numerical analysis, Halley’s method is a root-finding algorithm used for functions of one real variable with a continuous second derivative, i.e., C2 functions. It is named after its inventor Edmond Halley, who also discovered Halley's Comet....
,
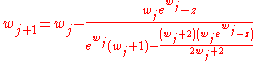
given in Corless et al. to compute W.
See also
- Lambert's trinomial equationTrinomialIn elementary algebra, a trinomial is a polynomial consisting of three terms or monomials.-Trinomial expressions:# 3x + 5y + 8z with x, y, z variables# 3t + 9s^2 + 3y^3 with t, s, y variables# 3ts + 9t + 5s with t, s variables...
- Lagrange inversion theorem
- Experimental mathematicsExperimental mathematicsExperimental mathematics is an approach to mathematics in which numerical computation is used to investigate mathematical objects and identify properties and patterns...
- R=T model
External links
- National Institute of Science and Technology Digital Library - Lambert W
- MathWorld - Lambert W-Function
- Computing the Lambert W function
- Corless et al. Notes about Lambert W research
- Extreme Mathematics. Monographs on the Lambert W function, its numerical approximation and generalizations for W-like inverses of transcendental forms with repeated exponential towers.
- GPL C++ implementation with Halley's and Fritsch's iteration.