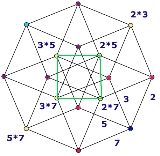
Hexany
Encyclopedia
Music theory
Music theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
, the hexany is a six-note just intonation
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
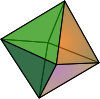
scale, with the notes placed on the vertices of an octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, equivalently the faces of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
. The notes are arranged so that every edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
of the octahedron joins together notes that make a consonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
dyad
Dyad (music)
In music, a dyad is a set of two notes or pitches. Although most chords have three or more notes, in certain contexts a dyad may be considered to be a chord. The most common two-note chord is made from the interval of a perfect fifth, which may be suggestive of music of the Medieval or Renaissance...
, and every face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
joins together the notes of a consonant triad
Triad (music)
In music and music theory, a triad is a three-note chord that can be stacked in thirds. Its members, when actually stacked in thirds, from lowest pitched tone to highest, are called:* the Root...
.
This makes a "musical geometry" with the geometrical form of the octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
. It has eight just intonation triads in a scale of only six notes, and each triad has two notes in common with three of the other chords, arranged in a musically symmetrical fashion due to the symmetry of the octahedron it is based on.
The Hexany is the invention of Erv Wilson
Erv Wilson
Ervin Wilson is a Mexican/American music theorist. Despite his avoidance of academia, Wilson has been influential on those interested in microtonal music and just intonation, especially in the areas of scale, keyboard, and notation design...
and represents one of the simplest structures found in his Combination Product Sets, which are obtained as successive cross sections of an n-dimensional cube. The numbers of vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
follow the numbers in Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
. The hexany is the third cross section of the four-dimensional cube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
. "Hexany is the name that Erv Wilson gave to the six notes in the 2-out-of-4 combination product set (abbreviated as 2\4 CPOS)."
Tuning
The four dimensions of the hypercube are usually tuned to distinct primesPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
(sometimes to odd numbers) and a single step in each dimension corresponds to multiplying the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
by that prime. The notes are then usually reduced to the octave (by repeated division by 2) using octave equivalence.
For example, for a 2 3 5 7 hexany, assign 2 3 5 7, to the four dimensions. Then to obtain the octahedron as a diagonal cross section of the hypercube, use all permutations of (1,1,0,0) as the coords. There for instance, (0,0,1,1) moves one step in the "5" dimension and one step in the "7" dimension and so would be tuned as 5×7.
So, to make the complete hexany, multiply the primes together in pairs to give six numbers: 2×3, 2×5, 2×7, 3×5, 3×7, and 5×7 (or 2×3×1×1, 2×1×5×1, 2×1×1×7, 1×3×5×1, 1×3×1×7 and 1×1×5×7). This shows the context in 4D.

In this picture of a hypercube, the six hexany vertices are shown in yellow, and four of the vertices are shown connected (in green). The other two vertices join to them to make the octahedron. All the sides of the octahedron are diagonals of squares, so are the same length (root two), so it is a regular octahedron — the "squashed" appearance is because it is rotated into the fourth dimension.
You can see the tetrahedral slices of the hypercube similarly - the red vertices can be joined together to make a regular tetrahedron, and the purple vertices likewise. So going from one of the blue points to the other you have 1 vertex, 4 for the red tetrahedron, 6 vertices for the yellow octahedron (hexany), 4 for the purple tetrahedron and 1 more vertex to make up the complete cube.
If one finds it a bit baffling that's to be expected — a few people, like Alicia Stott, have been able to think four-dimensionally but it is beyond most of us.
Then for example the face with vertices 3×5, 2×5, 5×7 is an otonal (major type) chord since it can be written as 5×(2, 3, 7), using low numbered harmonics
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
. The 5×7, 3×7, 3×5 is a utonal (minor type) chord since it can be written as 3×5×7×(1/3, 1/5, 1/7), using low-numbered subharmonic
Subharmonic
Subharmonic frequencies are frequencies below the fundamental frequency of an oscillator in a ratio of 1/n, with n a positive integer number. For example, if the fundamental frequency of an oscillator is 440 Hz, sub-harmonics include 220 Hz and 110 Hz...
s.
Musical lattices are often constructed with the octave dimension omitted. Then the hexanies show up in the 3D lattices as octahedra between the alternating otonal and utonal tetrahedra (for tetrads). However the octave (2) dimension is shown in the diagram above to bring out its 4D context, and help make the connection with the Pascal's triangle construction via the hypercube.
To make this into a conventional scale with 1/1 as the first note, first reduce all the notes to the octave. Since the scale doesn't have a 1/1 yet, choose one of the notes, it doesn't matter which. Let's choose 5×7. Divide all the notes by 5×7 to get: 1/1 8/7 6/5 48/35 8/5 12/7 2/1 (up to octave reduction). The ratios notation here shows the ratio of the frequencies of the notes. So for instance if the 1/1 is 500 hertz, then 6/5 is 600 hertz, and so forth.
This figure shows the hexany in its more usual 3D representation:
Relationship to Pascal's triangle
The complete row of Pascal's trianglePascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
for the hypercube in this construction runs 1 (single vertex), 4 (tetrahedron tetrad), 6 (hexany), 4 (another tetrad), 1. The idea generalises to other numbers of dimensions – for instance, the cross-sections of a five-dimensional cube give two versions of the dekany – a ten-note scale rich in tetrads, triads and dyads, which also contains many hexanies.
In six dimensions the same construction gives the twenty-note eikosany which is even richer in chords. It has pentads, tetrads, and triads as well as hexanies and dekanies.
In the case of the three-dimensional cube, it is usual to consider the entire cube as a single eight-note scale, the octany – the cross-sections then are 1, 3 (triad), 3 (another triad), 1, taken along any of the four main diagonals of the cube.
Coordinates for the Pascal's triangle of combination product sets
First row (square):00
10 01
11
Second row (cube or octony):
000
100 010 001 triad (triangle)
110 101 011 triad (triangle)
111
Third row (hypercube)
0000
1000 0100 0010 0001 tetrad (tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
or 3-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
)
1100 1010 1001 0110 0101 0011 hexany (octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
)
1110 1101 1011 0111 tetrad
1111
The octahedron there is the edge dual of the tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, or rectified
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
Fourth row (5-dimensional cube)
00000
10000 01000 00100 00010 00001 pentad (4-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
or pentachoron
Pentachoron
In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as the pentachoron, pentatope, or hyperpyramid...
- four dimensional tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
)
11000 10100 10010 10001 01100 01010 01001 00110 00101 00011 2)5 dekany (10 vertices, rectified
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
4-simplex)
00111 01011 01101 01110 10011 10101 10110 11001 11010 11100 3)5 dekany (10 vertices)
01111 10111 11011 11101 11110 pentad
11111
The rectified
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
4-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
for the dekany is also known as the dispentachoron
Fifth row (6-dimensional cube
000000
100000 010000 001000 000100 000010 000001 hexad (5-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
or hexateron
Hexateron
In five dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has 6 vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 pentachoron facets. It has a dihedral angle of cos−1, or approximately 78.46°.- Alternate names :...
- five dimensional tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
)
110000 101000 100100 100010 100001 011000 010100 010010 010001 001100 001010 001001 000110 000101 000011 2)6 pentadekany (15 vertices, rectified
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
5-simplex)
111000 110100 110010 110001 101100 101010 101001 100110 100101 100011
011100 011010 011001 010110 010101 010011 001110 001101 001011 000111 eikosany (20 vertices birectified 5-simplex)
001111 010111 011011 011101 011110 100111 101011 101101 101110 110011 110101 110110 111001 111010 111100 4)6 pentadekany (15 vertices)
011111 101111 110111 111011 111101 111110 hexad
111111
It is easy to see that the geometric figure for the dekany is the edge dual of the 4-simplex and the one for the pentadekany is the edge dual of the 5-simplex.
To see this, in the figure of the octahedron in the hypercube, scale the entire figure by 1/2 about the origin (blue vertex). The octahedron vertices will move to the midpoints of the original tetrahedron edges (joining the red vertices in the figure).
So - similarly the dekany vertices when scaled by 1/2 move to the midpoints of the 4-simplex edges, and the pentadekany vertices move to the midpoints of the 5-simplex edges, and so on in all the higher dimensions.
The eikosany vertices when scaled by 1/3 move to the centres of the 2D faces of the 5-simplex. To see that, note that in a 3D cube, 111 when scaled by 1/3 moves to the midpoint of 100 010 001 (each edge vector subtends the same distance along the long diagonal of the cube). So 11100 moves to the centre of the equilateral triangle with coords 10000 01000 00100 and similarly for all the other eikosany vertices.
So - the geometric figure for the eikosany is the 2D face dual of the 5-simplex or birectified 5-simplex. Similarly for the 3)7, 3)8 etc figures in all higher dimensions.
Similarly in eight dimensions, the figure you get using all permutations of 4 out of 8 is the 3D face dual of the 7-simplex, or 3-rectified 7-simplex (since 1111 scaled by 1/4 moves to the centre of the 3D regular tetrahedron face 1000 0100 0010 0001), and so on.
Composers
Composers including Kraig GradyKraig Grady
Kraig Grady is a US-Australian composer/sound artist. He has composed and performed with an ensemble of microtonal instruments of his own design and also worked as a shadow puppeteer, tuning theorist, filmmaker, world music radio DJ and concert promoter...
, Daniel James Wolf
Daniel James Wolf
Daniel James Wolf is an American composer.- Studies :Wolf studied composition with Gordon Mumma, Alvin Lucier, and La Monte Young, as well as musical tunings with Erv Wilson and Douglas Leedy and ethnomusicology . Important contacts with Lou Harrison, John Cage, Walter Zimmermann...
, and Joseph Pehrson
Joseph Pehrson
- Life :Pehrson comes from Detroit, Michigan. He studied at the University of Michigan and Eastman School of Music. . His teachers include Leslie Bassett, Joseph Schwantner, Otto Luening and Elie Siegmeister. From 1992 to 1993 he was composer-in-residence at the University of Akron. Since 1983 he...
have used pitch structures based on hexanies.
External links
- "Some Hexany and Hexany Diamond Lattices (and Blanks)", The Wilson Archives. Original Hexany papers showing different facets and configurations, not assembled by Erv Wilson (1967 on)
- "The Wilson Archives", Anaphoria.com
- "Hexany", RobertInventor.com. With a hexany you can turn around and click on any of its vertices, edges, or faces to hear the chords.
- "Combination-Product Set Patterns", Xenharmonikon IX (1986) by Kraig Grady.
- "Eikosany Papers", Anaphoria.com.
- "Musical Geometry", Music and Virtual Flowers. Intro. to musical geometry.
- "Alicia Boole Stott", The MacTutor History of Mathematics archive. Biography of Alicia Stott
- "The Tumbling Dekany", "Unusual musical scales", Dave Keenan's Home Page. Dave Keenan's Dekany tumbling in 4 dimensions — as a musical Excel spreadsheet

