
Grushko theorem
Encyclopedia
In the mathematical
subject of group theory
, the Grushko theorem or the Grushko-Neumann theorem is a theorem stating that the rank (that is, the smallest cardinality of a generating set
) of a free product
of two groups is equal to the sum of the ranks of the two free factors. The theorem was first obtained in a 1940 article of Grushko and then, independently, in a 1943 article of Neumann
.
of A and B. Then
It is obvious that rank(A∗B) ≤ rank(A) + rank(B) since if X is a finite generating set
of A and Y is a finite generating set of B then X∪Y is a generating set for A∗B and that |X∪Y|≤|X| + |Y|. The opposite inequality, rank(A∗B) ≥ rank(A) + rank(B), requires proof.
There is a more precise version of Grushko's theorem in terms of Nielsen equivalence. It states that if M = (g1, g2, ..., gn) is an n-tuple of elements of G = A∗B such that M generates G,1, g2, ..., gn> = G, then M is Nielsen equivalent in G to an n-tuple of the form
(1943), there were many subsequent alternative proofs, simplifications and generalizations of Grushko's theorem. A close version of Grushko's original proof is given in the 1955 book of Kurosh
.
Like the original proofs, Lyndon's proof (1965) relied on length-functions considerations but with substantial simplifications. A 1965 paper of Stallings
gave a greatly simplified topological proof of Grushko's theorem.
A 1970 paper of Zieschang gave a Nielsen equivalence version of Grushko's theorem (stated above) and provided some generalizations of Grushko's theorem for amalgamated free products. Scott (1974) gave another topological proof of Grushko's theorem, inspired by the methods of 3-manifold
topology Imrich (1984) gave a version of Grushko's theorem for free products with infinitely many factors.
Modern techniques of Bass-Serre theory, particularly the machinery of foldings for group actions on trees and for graphs of groups
provide a relatively straightforward proof of Grushko's theorem (see, for example ).
Grushko's theorem is, in a sense, a starting point in Dunwoody's theory of accessibility for finitely generated and finitely presented groups. Since the ranks of the free factors are smaller than the rank of a free product, Grushko's theorem implies that the process of iterated splitting of a finitely generated group G as a free product must terminate in a finite number of steps (more precisely, in at most rank(G) steps). There is a natural similar question for iterating splittings of finitely generated groups over finite subgroups. Dunwoody
proved that such a process must always terminate if a group G is finitely presented but may go on forever if G is finitely generated but not finitely presented.
An algebraic proof of a substantial generalization of Grushko's theorem using the machinery of groupoid
s was given by Higgins (1966). Higgins' theorem starts with groups G and B with free decompositions G = ∗i Gi, B = ∗i Bi and f : G → B a morphism such that f(Gi) = Bi for all i. Let H be a subgroup of G such that f(H) = B. Then H has a decomposition H = ∗i Hi such that f(Hi) = Bi for all i. Full details of the proof and applications may also be found in
.
where each of the groups Ai is nontrivial, freely indecomposable (that is, it cannot be decomposed as a free product) and not infinite cyclic, and where Fs is a free group
of rank s;
moreover, for a given G, the groups A1, ..., Ar are unique up to a permutation of their conjugacy class
es in G (and, in particular, the sequence of isomorphism
types of these groups is unique up to a permutation) and the numbers s and r are unique as well.
More precisely, if G = B1∗...∗Bk∗Ft is another such decomposition then k = r, s = t, and there exists a permutation
σ∈Sr such that for each i=1,...,r the subgroups Ai and Bσ(i) are conjugate
in G.
The existence of the above decomposition, called the Grushko decomposition of G, is an immediate corollary of the original Grushko theorem, while the uniqueness statement requires additional arguments (see, for example).
Algorithmically computing the Grushko decomposition for specific classes of groups is a difficult problem which primarily requires being able to determine if a given group is freely decomposable. Positive results are available for some classes of groups such as torsion-free word-hyperbolic groups, certain classes of relatively hyperbolic group
s, fundamental groups of finite graphs of finitely generated free groups and others.
Grushko decomposition theorem is a group-theoretic analog of the Kneser prime decomposition theorem
for 3-manifold
s which says that a closed 3-manifold can be uniquely decomposed as a connected sum
of irreducible 3-manifolds.
Let S={g1,....,gn} be a finite generating set for G=A∗B of size |S|=n=rank(G). Realize G as the fundamental group of a graph of groups Y which is a single non-loop edge with vertex groups A and B and with the trivial edge group. Let be the Bass-Serre covering tree for Y. Let F=F(x1,....,xn) be the free group
be the Bass-Serre covering tree for Y. Let F=F(x1,....,xn) be the free group
with free basis x1,....,xn and let φ0:F → G be the homomorphism
such that φ0(xi)=gi for i=1,...,n. Realize F as the fundamental group
of a graph Z0 which is the wedge of n circles that correspond to the elements x1,....,xn. We also think of Z0 as a graph of groups
with the underlying graph Z0 and the trivial vertex and edge groups. Then the universal cover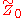 of Z0 and the Bass-Serre covering tree for Z0 coincide. Consider a φ0-equivariant map
of Z0 and the Bass-Serre covering tree for Z0 coincide. Consider a φ0-equivariant map 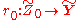 so that it sends vertices to vertices and edges to edge-paths. This map is non-injective and, since both the source and the target of the map are trees, this map "folds" some edge-pairs in the source. The graph of groups
so that it sends vertices to vertices and edges to edge-paths. This map is non-injective and, since both the source and the target of the map are trees, this map "folds" some edge-pairs in the source. The graph of groups
Z0 serves as an initial approximation for Y.
We now start performing a sequence of "folding moves" on Z0 (and on its Bass-Serre covering tree) to construct a sequence of graphs of groups
Z0, Z1, Z2, ...., that form better and better approximations for Y. Each of the graphs of groups Zj has trivial edge groups and comes with the following additional structure: for each nontrivial vertex group of it there assigned a finite generating set of that vertex group. The complexity c(Zj) of Zj is the sum of the sizes of the generating sets of its vertex groups and the rank of the free group π1(Zj). For the initial approximation graph we have c(Z0)=n.
The folding moves that take Zj to Zj+1 can be of one of two types:
One sees that the folding moves do not increase complexity but they do decrease the number of edges in Zj. Therefore the folding process must terminate in a finite number of steps with a graph of groups Zk that cannot be folded any more. It follows from the basic Bass-Serre theory considerations that Zk must in fact be equal to the edge of groups Y and that Zk comes equipped with finite generating sets for the vertex groups A and B. The sum of the sizes of these generating sets is the complexity of Zk which is therefore less than or equal to c(Z0)=n. This implies that the sum of the ranks of the vertex groups A and B is at most n, that is
rank(A)+rank(B)≤rank(G), as required.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
subject of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Grushko theorem or the Grushko-Neumann theorem is a theorem stating that the rank (that is, the smallest cardinality of a generating set
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
) of a free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
of two groups is equal to the sum of the ranks of the two free factors. The theorem was first obtained in a 1940 article of Grushko and then, independently, in a 1943 article of Neumann
Bernhard Neumann
Bernhard Hermann Neumann AC FRS was a German-born British mathematician who was one of the leading figures in group theory, greatly influencing the direction of the subject....
.
Statement of the theorem
Let A and B be finitely generated groups and let A∗B be the free productFree product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
of A and B. Then
- rank(A∗B) = rank(A) + rank(B).
It is obvious that rank(A∗B) ≤ rank(A) + rank(B) since if X is a finite generating set
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of A and Y is a finite generating set of B then X∪Y is a generating set for A∗B and that |X∪Y|≤|X| + |Y|. The opposite inequality, rank(A∗B) ≥ rank(A) + rank(B), requires proof.
There is a more precise version of Grushko's theorem in terms of Nielsen equivalence. It states that if M = (g1, g2, ..., gn) is an n-tuple of elements of G = A∗B such that M generates G,
- M = (a1, ..., ak, b1, ..., bn−k) where {a1, ..., ak}⊆A is a generating set for A and where {b1, ..., bn−k}⊆B is a generating set for B. In particular, rank(A) ≤ k, rank(B) ≤ n − k and rank(A) + rank(B) ≤ k + (n − k) = n. If one takes M to be the minimal generating tuple for G, that is, with n = rank(G), this implies that rank(A) + rank(B) ≤ rank(G). Since the opposite inequality, rank(G) ≤ rank(A) + rank(B), is obvious, it follows that rank(G)=rank(A) + rank(B), as required.
History and generalizations
After the original proofs of Grushko (1940) and NeumannBernhard Neumann
Bernhard Hermann Neumann AC FRS was a German-born British mathematician who was one of the leading figures in group theory, greatly influencing the direction of the subject....
(1943), there were many subsequent alternative proofs, simplifications and generalizations of Grushko's theorem. A close version of Grushko's original proof is given in the 1955 book of Kurosh
Aleksandr Gennadievich Kurosh
Aleksandr Gennadievich Kurosh was a Soviet mathematician, known for his work in abstract algebra. He is credited with writing the first modern and high-level text on group theory, his The Theory of Groups published in 1944.He was born in Yartsevo near Smolensk, and died in Moscow. He received his...
.
Like the original proofs, Lyndon's proof (1965) relied on length-functions considerations but with substantial simplifications. A 1965 paper of Stallings
gave a greatly simplified topological proof of Grushko's theorem.
A 1970 paper of Zieschang gave a Nielsen equivalence version of Grushko's theorem (stated above) and provided some generalizations of Grushko's theorem for amalgamated free products. Scott (1974) gave another topological proof of Grushko's theorem, inspired by the methods of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
topology Imrich (1984) gave a version of Grushko's theorem for free products with infinitely many factors.
Modern techniques of Bass-Serre theory, particularly the machinery of foldings for group actions on trees and for graphs of groups
Graph of groups
In geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
provide a relatively straightforward proof of Grushko's theorem (see, for example ).
Grushko's theorem is, in a sense, a starting point in Dunwoody's theory of accessibility for finitely generated and finitely presented groups. Since the ranks of the free factors are smaller than the rank of a free product, Grushko's theorem implies that the process of iterated splitting of a finitely generated group G as a free product must terminate in a finite number of steps (more precisely, in at most rank(G) steps). There is a natural similar question for iterating splittings of finitely generated groups over finite subgroups. Dunwoody
Martin Dunwoody
Martin John Dunwoody is an Emeritus Professor of mathematics at the University of Southampton, England.He earned his Ph.D. in 1964 from the Australian National University. He held positions at the University of Sussex before becoming full Professor at the University of Southampton in 1992...
proved that such a process must always terminate if a group G is finitely presented but may go on forever if G is finitely generated but not finitely presented.
An algebraic proof of a substantial generalization of Grushko's theorem using the machinery of groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
s was given by Higgins (1966). Higgins' theorem starts with groups G and B with free decompositions G = ∗i Gi, B = ∗i Bi and f : G → B a morphism such that f(Gi) = Bi for all i. Let H be a subgroup of G such that f(H) = B. Then H has a decomposition H = ∗i Hi such that f(Hi) = Bi for all i. Full details of the proof and applications may also be found in
.
Grushko decomposition theorem
A useful consequence of the original Grushko theorem is the so-called Grushko decomposition theorem. It asserts that any nontrivial finitely generated group G can be decomposed as a free productFree product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
- G = A1∗A2∗...∗Ar∗Fs, where s ≥ 0, r ≥ 0,
where each of the groups Ai is nontrivial, freely indecomposable (that is, it cannot be decomposed as a free product) and not infinite cyclic, and where Fs is a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of rank s;
moreover, for a given G, the groups A1, ..., Ar are unique up to a permutation of their conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es in G (and, in particular, the sequence of isomorphism
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
types of these groups is unique up to a permutation) and the numbers s and r are unique as well.
More precisely, if G = B1∗...∗Bk∗Ft is another such decomposition then k = r, s = t, and there exists a permutation
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
σ∈Sr such that for each i=1,...,r the subgroups Ai and Bσ(i) are conjugate
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
in G.
The existence of the above decomposition, called the Grushko decomposition of G, is an immediate corollary of the original Grushko theorem, while the uniqueness statement requires additional arguments (see, for example).
Algorithmically computing the Grushko decomposition for specific classes of groups is a difficult problem which primarily requires being able to determine if a given group is freely decomposable. Positive results are available for some classes of groups such as torsion-free word-hyperbolic groups, certain classes of relatively hyperbolic group
Relatively hyperbolic group
In mathematics, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory concept of a hyperbolic group...
s, fundamental groups of finite graphs of finitely generated free groups and others.
Grushko decomposition theorem is a group-theoretic analog of the Kneser prime decomposition theorem
Prime decomposition (3-manifold)
In mathematics, the prime decomposition theorem for 3-manifolds states that every compact, orientable 3-manifold is the connected sum of a unique collection of prime 3-manifolds....
for 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s which says that a closed 3-manifold can be uniquely decomposed as a connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
of irreducible 3-manifolds.
Sketch of the proof using Bass-Serre theory
The following is a sketch of the proof of Grushko's theorem based on the use of foldings techniques for groups acting on trees (see for complete proofs using this argument).Let S={g1,....,gn} be a finite generating set for G=A∗B of size |S|=n=rank(G). Realize G as the fundamental group of a graph of groups Y which is a single non-loop edge with vertex groups A and B and with the trivial edge group. Let
 be the Bass-Serre covering tree for Y. Let F=F(x1,....,xn) be the free group
be the Bass-Serre covering tree for Y. Let F=F(x1,....,xn) be the free groupFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
with free basis x1,....,xn and let φ0:F → G be the homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
such that φ0(xi)=gi for i=1,...,n. Realize F as the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a graph Z0 which is the wedge of n circles that correspond to the elements x1,....,xn. We also think of Z0 as a graph of groups
Graph of groups
In geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
with the underlying graph Z0 and the trivial vertex and edge groups. Then the universal cover
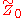 of Z0 and the Bass-Serre covering tree for Z0 coincide. Consider a φ0-equivariant map
of Z0 and the Bass-Serre covering tree for Z0 coincide. Consider a φ0-equivariant map 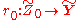 so that it sends vertices to vertices and edges to edge-paths. This map is non-injective and, since both the source and the target of the map are trees, this map "folds" some edge-pairs in the source. The graph of groups
so that it sends vertices to vertices and edges to edge-paths. This map is non-injective and, since both the source and the target of the map are trees, this map "folds" some edge-pairs in the source. The graph of groupsGraph of groups
In geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
Z0 serves as an initial approximation for Y.
We now start performing a sequence of "folding moves" on Z0 (and on its Bass-Serre covering tree) to construct a sequence of graphs of groups
Graph of groups
In geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
Z0, Z1, Z2, ...., that form better and better approximations for Y. Each of the graphs of groups Zj has trivial edge groups and comes with the following additional structure: for each nontrivial vertex group of it there assigned a finite generating set of that vertex group. The complexity c(Zj) of Zj is the sum of the sizes of the generating sets of its vertex groups and the rank of the free group π1(Zj). For the initial approximation graph we have c(Z0)=n.
The folding moves that take Zj to Zj+1 can be of one of two types:
- folds that identify two edges of the underlying graph with a common initial vertex but distinct end-vertices into a single edge; when such a fold is performed, the generating sets of the vertex groups and the terminal edges are "joined" together into a generating set of the new vertex group; the rank of the fundamental group of the underlying graph does not change under such a move.
- folds that identify two edges, that already had common initial vertices and common terminal vertices, into a single edge; such a move decreases the rank of the fundamental group of the underlying graph by 1 and an element that corresponded to the loop in the graph that is being collapsed is "added" to the generating set of one of the vertex groups.
One sees that the folding moves do not increase complexity but they do decrease the number of edges in Zj. Therefore the folding process must terminate in a finite number of steps with a graph of groups Zk that cannot be folded any more. It follows from the basic Bass-Serre theory considerations that Zk must in fact be equal to the edge of groups Y and that Zk comes equipped with finite generating sets for the vertex groups A and B. The sum of the sizes of these generating sets is the complexity of Zk which is therefore less than or equal to c(Z0)=n. This implies that the sum of the ranks of the vertex groups A and B is at most n, that is
rank(A)+rank(B)≤rank(G), as required.

