
Connected sum
Encyclopedia
In mathematics
, specifically in topology
, the operation of connected sum is a geometric modification on manifold
s. Its effect is to join two given manifolds together near a chosen point on each. This construction plays a key role in the classification of closed surfaces.
More generally, one can also join manifolds together along identical submanifolds; this generalization is often called the fiber sum. There is also a closely related notion of a connected sum on knot
s, called the knot sum or composition of knots.

s is a manifold formed by deleting a ball
inside each manifold and gluing together
the resulting boundary sphere
s.
If both manifolds are oriented, there is a unique connected sum defined by having the gluing map reverse orientation. Although the construction uses the choice of the balls, the result is unique up to homeomorphism
. One can also make this operation work in the smooth
category
, and then the result is unique up to diffeomorphism
. There are subtle problems in the smooth case: not every diffeomorphism between the boundaries of the spheres gives the same composite manifold, even if the orientations are chosen correctly. For example, Milnor showed that two 7-cells can be glued along their boundary so that the result is an exotic sphere
homeomorphic but not diffeomorphic to a 7-sphere. However there is a canonical way to choose the gluing which gives a unique well defined connected sum. This uniqueness depends crucially on the disc theorem
, which is not at all obvious.
The operation of connected sum is denoted by ; for example
; for example  denotes the connected sum of
denotes the connected sum of  and
and  .
.
The operation of connected sum has the sphere as an identity
as an identity
; that is, is homeomorphic (or diffeomorphic) to
is homeomorphic (or diffeomorphic) to  .
.
The classification of closed surfaces, a foundational and historically significant result in topology, states that any closed surface can be expressed as the connected sum of a sphere with some number of tori
of tori
and some number of real projective plane
of real projective plane
s.
 and
and  be two smooth, oriented manifolds of equal dimension and
be two smooth, oriented manifolds of equal dimension and  a smooth, closed, oriented manifold, embedded as a submanifold into both
a smooth, closed, oriented manifold, embedded as a submanifold into both  and
and  . Suppose furthermore that there exists an isomorphism of normal bundle
. Suppose furthermore that there exists an isomorphism of normal bundle
s

that reverses the orientation on each fiber. Then induces an orientation-preserving diffeomorphism
induces an orientation-preserving diffeomorphism

where each normal bundle is diffeomorphically identified with a neighborhood
is diffeomorphically identified with a neighborhood  of
of  in
in  , and the map
, and the map

is the orientation-reversing diffeomorphic involution

on normal vectors. The connected sum of and
and  along
along  is then the space
is then the space

obtained by gluing the deleted neighborhoods together by the orientation-preserving diffeomorphism. The sum is often denoted

Its diffeomorphism type depends on the choice of the two embeddings of and on the choice of
and on the choice of  .
.
Loosely speaking, each normal fiber of the submanifold contains a single point of
contains a single point of  , and the connected sum along
, and the connected sum along  is simply the connected sum as described in the preceding section, performed along each fiber. For this reason, the connected sum along
is simply the connected sum as described in the preceding section, performed along each fiber. For this reason, the connected sum along  is often called the fiber sum.
is often called the fiber sum.
The special case of a point recovers the connected sum of the preceding section.
a point recovers the connected sum of the preceding section.
 is two less than that of the
is two less than that of the  . Then the isomorphism
. Then the isomorphism  of normal bundles exists whenever their Euler class
of normal bundles exists whenever their Euler class
es are opposite:

Furthermore, in this case the structure group of the normal bundles is the circle group ; it follows that the choice of embeddings can be canonically identified with the group of homotopy
; it follows that the choice of embeddings can be canonically identified with the group of homotopy
classes of maps from to the circle, which in turn equals the first integral cohomology
to the circle, which in turn equals the first integral cohomology
group . So the diffeomorphism type of the sum depends on the choice of
. So the diffeomorphism type of the sum depends on the choice of  and a choice of element from
and a choice of element from  .
.
A connected sum along a codimension-two can also be carried out in the category of symplectic manifold
can also be carried out in the category of symplectic manifold
s; this elaboration is called the symplectic sum
.
 . This implies, for example, that the sum can be carried out on a single manifold
. This implies, for example, that the sum can be carried out on a single manifold  containing two disjoint copies of
containing two disjoint copies of  , with the effect of gluing
, with the effect of gluing  to itself. For example, the connected sum of a two-sphere at two distinct points of the sphere produces the two-torus.
to itself. For example, the connected sum of a two-sphere at two distinct points of the sphere produces the two-torus.
into the ambient space
. So the connected sum of knots has a more elaborate definition that produces a well-defined embedding, as follows.
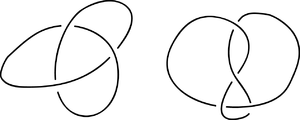
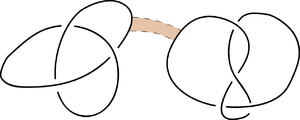
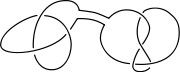 This procedure results in the projection of a new knot, a connected sum (or knot sum, or composition) of the original knots. For the connected sum of knots to be well defined, one has to consider oriented knots in 3-space. To define the connected sum for two oriented knots:
This procedure results in the projection of a new knot, a connected sum (or knot sum, or composition) of the original knots. For the connected sum of knots to be well defined, one has to consider oriented knots in 3-space. To define the connected sum for two oriented knots:
The resulting connected sum knot inherits an orientation consistent with the orientations of the two original knots, and the oriented ambient isotopy class of the result is well-defined, depending only on the oriented ambient isotopy classes of the original two knots.
Under this operation, oriented knots in 3-space form a commutative monoid
with unique prime factorization, which allows us to define what is meant by a prime knot
. Proof of commutativity can be seen by letting one summand shrink until it is very small and then pulling it along the other knot. The unknot is the unit. The two trefoil knots are the simplest prime knot
s. Higher dimensional knots can be added by splicing the -spheres.
-spheres.
In three dimensions, the unknot cannot be written as the sum of two non-trivial knots. This fact follows from additivity of knot genus; another proof relies on an infinite construction sometimes called the Mazur swindle. In higher dimensions (with codimension at least three), it is possible to get an unknot by adding two nontrivial knots.
If one does not take into account the orientations of the knots, the connected sum operation is not well defined on isotopy classes of (nonoriented) knots. To see this, consider two noninvertible knots K, L which are not equivalent (as unoriented knots); for example take the two pretzel knots K = P(3,5,7) and L = P(3,5,9). Let K+ and K- be K with its two inequivalent orientations, and let L+ and L- be L with its two inequivalent orientations. There are four oriented connected sums we may form:
The oriented ambient istotopy classes of these four oriented knots are all distinct. And, when one considers ambient isotopy of the knots without regard to orientation, there are two distinct equivalence classes: { A ~ B } and { C ~ D }. To see that A and B are unoriented equivalent, simply note that they both may be constructed from the same pair of disjoint knot projections as above, the only difference being the orientations of the knots. Similarly, one sees that C and D may be constructed from the same pair of disjoint knot projections.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the operation of connected sum is a geometric modification on manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. Its effect is to join two given manifolds together near a chosen point on each. This construction plays a key role in the classification of closed surfaces.
More generally, one can also join manifolds together along identical submanifolds; this generalization is often called the fiber sum. There is also a closely related notion of a connected sum on knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
s, called the knot sum or composition of knots.

Connected sum at a point
A connected sum of two m-dimensional manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s is a manifold formed by deleting a ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
inside each manifold and gluing together
Adjunction space
In mathematics, an adjunction space is a common construction in topology where one topological space is attached or "glued" onto another. Specifically, let X and Y be a topological spaces with A a subspace of Y. Let f : A → X be a continuous map...
the resulting boundary sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s.
If both manifolds are oriented, there is a unique connected sum defined by having the gluing map reverse orientation. Although the construction uses the choice of the balls, the result is unique up to homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
. One can also make this operation work in the smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
, and then the result is unique up to diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
. There are subtle problems in the smooth case: not every diffeomorphism between the boundaries of the spheres gives the same composite manifold, even if the orientations are chosen correctly. For example, Milnor showed that two 7-cells can be glued along their boundary so that the result is an exotic sphere
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
homeomorphic but not diffeomorphic to a 7-sphere. However there is a canonical way to choose the gluing which gives a unique well defined connected sum. This uniqueness depends crucially on the disc theorem
Disc theorem
In the area of mathematics known as differential topology, the disc theorem of states that two embeddings of a closed k-disc into a connected n-manifold are ambient isotopic provided that if k = n the two embeddings are equioriented....
, which is not at all obvious.
The operation of connected sum is denoted by
 ; for example
; for example  denotes the connected sum of
denotes the connected sum of  and
and  .
.The operation of connected sum has the sphere
 as an identity
as an identityIdentity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
; that is,
 is homeomorphic (or diffeomorphic) to
is homeomorphic (or diffeomorphic) to  .
.The classification of closed surfaces, a foundational and historically significant result in topology, states that any closed surface can be expressed as the connected sum of a sphere with some number
 of tori
of toriTorus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
and some number
 of real projective plane
of real projective planeReal projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
s.
Connected sum along a submanifold
Let and
and  be two smooth, oriented manifolds of equal dimension and
be two smooth, oriented manifolds of equal dimension and  a smooth, closed, oriented manifold, embedded as a submanifold into both
a smooth, closed, oriented manifold, embedded as a submanifold into both  and
and  . Suppose furthermore that there exists an isomorphism of normal bundle
. Suppose furthermore that there exists an isomorphism of normal bundleNormal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
s

that reverses the orientation on each fiber. Then
 induces an orientation-preserving diffeomorphism
induces an orientation-preserving diffeomorphism
where each normal bundle
 is diffeomorphically identified with a neighborhood
is diffeomorphically identified with a neighborhood  of
of  in
in  , and the map
, and the map
is the orientation-reversing diffeomorphic involution

on normal vectors. The connected sum of
 and
and  along
along  is then the space
is then the space
obtained by gluing the deleted neighborhoods together by the orientation-preserving diffeomorphism. The sum is often denoted

Its diffeomorphism type depends on the choice of the two embeddings of
 and on the choice of
and on the choice of  .
.Loosely speaking, each normal fiber of the submanifold
 contains a single point of
contains a single point of  , and the connected sum along
, and the connected sum along  is simply the connected sum as described in the preceding section, performed along each fiber. For this reason, the connected sum along
is simply the connected sum as described in the preceding section, performed along each fiber. For this reason, the connected sum along  is often called the fiber sum.
is often called the fiber sum.The special case of
 a point recovers the connected sum of the preceding section.
a point recovers the connected sum of the preceding section.Connected sum along a codimension-two submanifold
Another important special case occurs when the dimension of is two less than that of the
is two less than that of the  . Then the isomorphism
. Then the isomorphism  of normal bundles exists whenever their Euler class
of normal bundles exists whenever their Euler classEuler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
es are opposite:

Furthermore, in this case the structure group of the normal bundles is the circle group
 ; it follows that the choice of embeddings can be canonically identified with the group of homotopy
; it follows that the choice of embeddings can be canonically identified with the group of homotopyHomotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
classes of maps from
 to the circle, which in turn equals the first integral cohomology
to the circle, which in turn equals the first integral cohomologyCohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
group
 . So the diffeomorphism type of the sum depends on the choice of
. So the diffeomorphism type of the sum depends on the choice of  and a choice of element from
and a choice of element from  .
.A connected sum along a codimension-two
 can also be carried out in the category of symplectic manifold
can also be carried out in the category of symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s; this elaboration is called the symplectic sum
Symplectic sum
In mathematics, specifically in symplectic geometry, the symplectic sum is a geometric modification on symplectic manifolds, which glues two given manifolds into a single new one. It is a symplectic version of connected summation along a submanifold, often called a fiber sum.The symplectic sum is...
.
Local operation
The connected sum is a local operation on manifolds, meaning that it alters the summands only in a neighborhood of . This implies, for example, that the sum can be carried out on a single manifold
. This implies, for example, that the sum can be carried out on a single manifold  containing two disjoint copies of
containing two disjoint copies of  , with the effect of gluing
, with the effect of gluing  to itself. For example, the connected sum of a two-sphere at two distinct points of the sphere produces the two-torus.
to itself. For example, the connected sum of a two-sphere at two distinct points of the sphere produces the two-torus.Connected sum of knots
There is a closely related notion of the connected sum of two knots. In fact, if one regards a knot merely as a one-manifold, then the connected sum of two knots is just their connected sum as a one-dimensional manifold. However, the essential property of a knot is not its manifold structure (all knots are circles) but rather its embeddingEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
into the ambient space
Ambient space
An ambient space, ambient configuration space, or electroambient space, is the space surrounding an object.-Mathematics:In mathematics, especially in geometry and topology, an ambient space is the space surrounding a mathematical object...
. So the connected sum of knots has a more elaborate definition that produces a well-defined embedding, as follows.
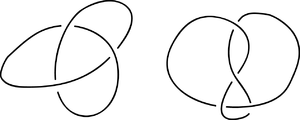


- Consider a planar projection of each knot and suppose these projections are disjoint.
- Find a rectangle in the plane where one pair of sides are arcs along each knot but is otherwise disjoint from the knots and so that the arcs of the knots on the sides of the rectangle are oriented around the boundary of the rectangle in the same direction.
- Now join the two knots together by deleting these arcs from the knots and adding the arcs that form the other pair of sides of the rectangle.
The resulting connected sum knot inherits an orientation consistent with the orientations of the two original knots, and the oriented ambient isotopy class of the result is well-defined, depending only on the oriented ambient isotopy classes of the original two knots.
Under this operation, oriented knots in 3-space form a commutative monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
with unique prime factorization, which allows us to define what is meant by a prime knot
Prime knot
In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
. Proof of commutativity can be seen by letting one summand shrink until it is very small and then pulling it along the other knot. The unknot is the unit. The two trefoil knots are the simplest prime knot
Prime knot
In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
s. Higher dimensional knots can be added by splicing the
 -spheres.
-spheres.In three dimensions, the unknot cannot be written as the sum of two non-trivial knots. This fact follows from additivity of knot genus; another proof relies on an infinite construction sometimes called the Mazur swindle. In higher dimensions (with codimension at least three), it is possible to get an unknot by adding two nontrivial knots.
If one does not take into account the orientations of the knots, the connected sum operation is not well defined on isotopy classes of (nonoriented) knots. To see this, consider two noninvertible knots K, L which are not equivalent (as unoriented knots); for example take the two pretzel knots K = P(3,5,7) and L = P(3,5,9). Let K+ and K- be K with its two inequivalent orientations, and let L+ and L- be L with its two inequivalent orientations. There are four oriented connected sums we may form:
- A = K+ # L+
- B = K- # L-
- C = K+ # L-
- D = K- # L+
The oriented ambient istotopy classes of these four oriented knots are all distinct. And, when one considers ambient isotopy of the knots without regard to orientation, there are two distinct equivalence classes: { A ~ B } and { C ~ D }. To see that A and B are unoriented equivalent, simply note that they both may be constructed from the same pair of disjoint knot projections as above, the only difference being the orientations of the knots. Similarly, one sees that C and D may be constructed from the same pair of disjoint knot projections.
See also
- Band sumBand sumIn geometric topology, a band sum of two n-dimensional knots K1 and K2 along an -dimensional 1-handle h called a band is an n-dimensional knot K such that:...
- Prime decomposition (3-manifold)Prime decomposition (3-manifold)In mathematics, the prime decomposition theorem for 3-manifolds states that every compact, orientable 3-manifold is the connected sum of a unique collection of prime 3-manifolds....
- Manifold decompositionManifold decompositionIn topology, a branch of mathematics, a manifold M may be decomposed or split by writing M as a combination of smaller pieces. When doing so, one must specify both what those pieces are and how they are put together to form M....
- Satellite knotSatellite knotIn the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non-boundary parallel torus in its complement. The class of satellite knots include composite knots, cable knots and Whitehead doubles. A satellite knot K can be picturesquely described as follows:...

