
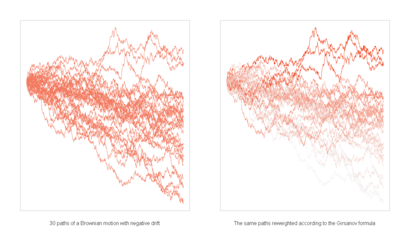
Girsanov theorem
Encyclopedia
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the Girsanov theorem (named after Igor Vladimirovich Girsanov
Igor Vladimirovich Girsanov
Igor Vladimirovich Girsanov was a Russian mathematician. He made major contributions to probability theory and its applications.- Early life :...
) describes how the dynamics of stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es change when the original measure is changed to an equivalent probability measure
Equivalence (measure theory)
In mathematics, and specifically in measure theory, equivalence is a notion of two measures being "the same".-Definition:Let be a measurable space, and let μ, ν : Σ → R be two signed measures. Then μ is said to be equivalent to ν if and only if each is absolutely continuous with respect to the other...
. The theorem is especially important in the theory of financial mathematics as it tells how to convert from the physical measure which describes the probability that an underlying instrument (such as a share
Stock
The capital stock of a business entity represents the original capital paid into or invested in the business by its founders. It serves as a security for the creditors of a business since it cannot be withdrawn to the detriment of the creditors...
price or interest rate
Interest rate
An interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
) will take a particular value or values to the risk-neutral measure
Risk-neutral measure
In mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
which is a very useful tool for pricing derivatives
Derivative (finance)
A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
on the underlying.
History
Results of this type were first proved by Cameron–Martin in the 1940s and by Girsanov in 1960. They have been subsequently extended to more general classes of process culminating in the general form of Lenglart (1977).Significance
Girsanov's theorem is important in the general theory of stochastic processes since it enables the key result that if Q is a measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
absolutely continuous
Absolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
with respect to P then every P-semimartingale
Semimartingale
In probability theory, a real valued process X is called a semimartingale if it can be decomposed as the sum of a local martingale and an adapted finite-variation process....
is a Q-semimartingale.
Statement of theorem
We state the theorem first for the special case when the underlying stochastic process is a Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
. This special case is sufficient for risk-neutral pricing in the Black-Scholes model and in many other models (e.g. all continuous models).
Let
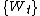 be a Wiener process on the Wiener probability space
be a Wiener process on the Wiener probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
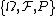 . Let
. Let 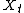 be a measurable process adapted
be a measurable process adaptedAdapted process
In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...
to the natural filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
of the Wiener process
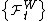 .
.Given an adapted process
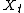 with
with 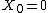 define
define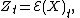
where
 is the stochastic exponential (or Doléans exponential) of X with respect to W, i.e.
is the stochastic exponential (or Doléans exponential) of X with respect to W, i.e.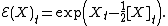
Thus
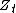 is a strictly positive local martingale
is a strictly positive local martingaleLocal martingale
In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; however, in general a local martingale is not a martingale, because its...
, and a probability
measure Q can be defined on
 such that we have Radon–Nikodym derivative
such that we have Radon–Nikodym derivative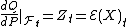
Then for each t the measure Q restricted to the unaugmented sigma fields
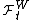 is equivalent to P restricted to
is equivalent to P restricted to 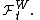
Furthermore if Y is a local martingale under P then the process
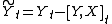
is a Q local martingale on the filtered probability space
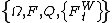 .
.Corollary
If X is a continuous process and W is Brownian Motion under measure P then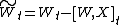
is Brownian motion under Q.
The fact that
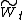 is continuous is trivial; by Girsanov's theorem it is a Q local martingale, and by computing the quadratic variation
is continuous is trivial; by Girsanov's theorem it is a Q local martingale, and by computing the quadratic variationQuadratic variation
In mathematics, quadratic variation is used in the analysis of stochastic processes such as Brownian motion and martingales. Quadratic variation is just one kind of variation of a process.- Definition :...

it follows by Levy's characterization of Brownian Motion that this is a Q Brownian
Motion.
Comments
In many common applications, the process X is defined by
For X of this form then a sufficient condition for
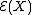 to be a martingale is Novikov's condition
to be a martingale is Novikov's conditionNovikov's condition
In probability theory, Novikov's condition is the sufficient condition for a stochastic process which takes the form of the Radon-Nikodym derivative in Girsanov's theorem to be a martingale...
which requires that
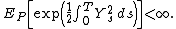
The stochastic exponential
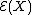 is the process Z which solves the stochastic differential equation
is the process Z which solves the stochastic differential equation
The measure Q constructed above is not equivalent to P on
 as this would only be the case if the Radon–Nikodym derivative
as this would only be the case if the Radon–Nikodym derivativeRadon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
were a uniformly integrable martingale, which the exponential martingale described above is not (for
 ).
).Application to finance
In finance, Girsanov theorem is used each time one needs to derive an asset's or rate's dynamics under a new probability measure. The most well known case is moving from historic measure P to risk neutral measure Q which is done - in Black Scholes framework - via Radon–Nikodym derivativeRadon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
:
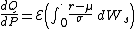
where r denotes the instanteaneous risk free rate,
 the asset's drift and
the asset's drift and  its volatility.
its volatility.Other classical applications of Girsanov theorem are quanto adjustments and the calculation of forwards' drifts under Libor Market Model.
External links
- Notes on Stochastic Calculus which contains a simple outline proof of Girsanov's theorem.
- Applied Multidimensional Girsanov Theorem which contains financial applications of Girsanov's theorem.

