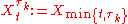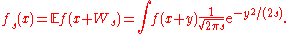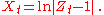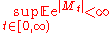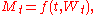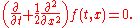In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a local martingale is a type of stochastic process

Stochastic process

In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...

, satisfying the localized version of the martingale

Martingale (probability theory)

In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...

 property. Every martingale is a local martingale; every bounded local martingale is a martingale; however, in general a local martingale is not a martingale, because its expectation can be distorted by large values of small probability. In particular, a driftless diffusion process

Ito diffusion

In mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...

 is a local martingale, but not necessarily a martingale.

Local martingales are essential in stochastic analysis, see Itō calculus, semimartingale

Semimartingale

In probability theory, a real valued process X is called a semimartingale if it can be decomposed as the sum of a local martingale and an adapted finite-variation process....

, Girsanov theorem

Girsanov theorem

In probability theory, the Girsanov theorem describes how the dynamics of stochastic processes change when the original measure is changed to an equivalent probability measure...

.

Definition

Let (Ω, F, P) be a probability space

Probability space

In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...

; let F_∗ = { F_t | t ≥ 0 } be a filtration

Filtration (abstract algebra)

In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...

 of F; let X : [0, +∞) × Ω → S be an F_∗-adapted stochastic process

Adapted process

In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...

. Then X is called an F_∗-local martingale if there exists a sequence of F_∗-stopping times

Stopping rule

In probability theory, in particular in the study of stochastic processes, a stopping time is a specific type of “random time”....

 τ_k : Ω → [0, +∞) such that

• the τ_k are almost surely
  Almost surely
  In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
  
   increasing: P[τ_k < τ_k+1] = 1;
• the τ_k diverge almost surely: P[τ_k → +∞ as k → +∞] = 1;
• the stopped process
  Stopped process
  In mathematics, a stopped process is a stochastic process that is forced to assume the same value after a prescribed time.-Definition:Let* be a probability space;...
  
  

is an F_∗-martingale for every k.

Example 1

Let W_t be the Wiener process

Wiener process

In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...

 and T = min{ t : W_t = −1 } the time of first hit

Hitting time

In the study of stochastic processes in mathematics, a hitting time is a particular instance of a stopping time, the first time at which a given process "hits" a given subset of the state space...

 of −1. The stopped process

Stopped process

In mathematics, a stopped process is a stochastic process that is forced to assume the same value after a prescribed time.-Definition:Let* be a probability space;...

 W_{min{ t, T }} is a martingale; its expectation is 0 at all times, nevertheless its limit (as t → ∞) is equal to −1 almost surely (a kind of gambler's ruin

Gambler's ruin

The term gambler's ruin is used for a number of related statistical ideas:* The original meaning is that a gambler who raises his bet to a fixed fraction of bankroll when he wins, but does not reduce it when he loses, will eventually go broke, even if he has a positive expected value on each bet.*...

). A time change leads to a process

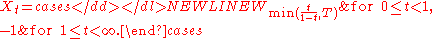
The process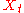 is continuous almost surely; nevertheless, its expectation is discontinuous,

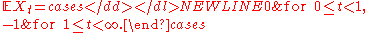
This process is not a martingale. However, it is a local martingale. A localizing sequence may be chosen as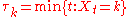 if there is such t, otherwise τ_k = k. This sequence diverges almost surely, since τ_k = k for all k large enough (namely, for all k that exceed the maximal value of the process X). The process stopped at τ_k is a martingale.
For the times before 1 it is a martingale since a stopped Brownian motion is. After the instant 1 it is constant. It remains to check it at the instant 1. By the bounded convergence theorem the expectation at 1 is the limit of the expectation at (n-1)/n (as n tends to infinity), and the latter does not depend on n. The same argument applies to the conditional expectation.

Example 2

Let W_t be the Wiener process

Wiener process

In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...

 and ƒ a measurable function such that Then the following process is a martingale:

here

The Dirac delta function

Dirac delta function

The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...

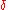  (strictly speaking, not a function), being used in place of 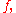leads to a process defined informally as 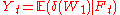and formally as

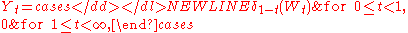
where

The process is continuous almost surely (since 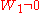almost surely), nevertheless, its expectation is discontinuous,

This process is not a martingale. However, it is a local martingale. A localizing sequence may be chosen as

Example 3

Let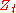 be the complex-valued Wiener process, and

The process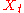 is continuous almost surely (since 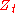does not hit 1, almost surely), and is a local martingale, since the function is harmonic

Harmonic function

In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....

 (on the complex plane without the point 1). A localizing sequence may be chosen as Nevertheless, the expectation of this process is non-constant; moreover,

  as

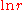which can be deduced from the fact that the mean value of over the circle tends to infinity as . (In fact, it is equal to for r ≥ 1 but to 0 for r ≤ 1).

Martingales via local martingales

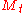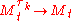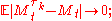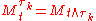Let be a local martingale. In order to prove that it is a martingale it is sufficient to prove that in L¹ (as ) for every t, that is, here is the stopped process. The given relation implies that 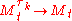almost surely. The dominated convergence theorem

Dominated convergence theorem

In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...

 ensures the convergence in L¹ provided that

   for every t.

Thus, Condition (*) is sufficient for a local martingale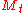 being a martingale. A stronger condition

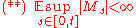   for every t

is also sufficient.

Caution. The weaker condition

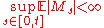   for every t

is not sufficient. Moreover, the condition

is still not sufficient; for a counterexample see Example 3 above.

A special case:

where is the Wiener process

Wiener process

In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...

, and is twice continuously differentiable

Smooth function

In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...

. The process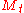 is a local martingale if and only if f satisfies the PDE

Partial differential equation

In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...

However, this PDE itself does not ensure that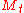 is a martingale. In order to apply (**) the following condition on f is sufficient: for every and t there exists such that

for all and

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.