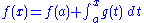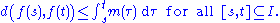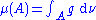Absolute continuity
Encyclopedia
In mathematics
, the relationship between the two central operations of calculus
, differentiation
and integration
, stated by fundamental theorem of calculus
in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration
and absolute continuity. For real-valued functions on the real line
two interrelated notions appear, absolute continuity of functions and absolute continuity of measures. These two notions are generalized in different directions. The usual derivative of a function is related to the Radon–Nikodym derivative, or density, of a measure.
, which means that this function is not absolutely continuous. Absolute continuity of functions is a smoothness property which is stricter than continuity
and uniform continuity
.
in the real line
R. A function f: I → R is absolutely continuous on I if for every positive number
, there is a positive number 
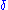such that whenever a finite sequence of pairwise disjoint sub-intervals (xk, yk) of I satisfies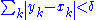
then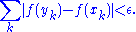
The collection of all absolutely continuous functions on I is denoted AC(I).
f is absolutely continuous;
f has a derivative f ′ almost everywhere
, the derivative is Lebesgue integrable, and
there exists a Lebesgue integrable function g on [a,b] such that
If these equivalent conditions are satisfied then necessarily g = f ′ almost everywhere.
Equivalence between (1) and (3) is known as the fundamental theorem of Lebesgue integral calculus, due to Lebesgue.
For an equivalent definition in terms of measures see the section Relation between the two notions of absolute continuity.
and let I be an interval
in the real line
R. A function f: I → X is absolutely continuous on I if for every positive number
, there is a positive number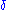 
such that whenever a finite sequence of pairwise disjoint sub-intervals [xk, yk] of I satisfies
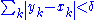
then
The collection of all absolutely continuous functions from I into X is denoted AC(I; X).
A further generalization is the space ACp(I; X) of curves f: I → X such that
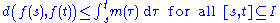
for some m in the Lp space
Lp(I).
μ on Borel subsets
of the real line is absolutely continuous with respect to Lebesgue measure
λ (in other words, dominated by λ) if μ(A) = 0 for every set A for which λ(A) = 0. This is written as “μ << λ”.
In most applications, if a measure on the real line is simply said to be absolutely continuous — without specifying with respect to which other measure it is absolutely continuous — then absolute continuity with respect to Lebesgue measure is meant.
The same holds for Rn for all n=1,2,3,...
μ is absolutely continuous;
for every positive number ε there is a positive number δ such that μ(A) < ε for all Borel sets A of Lebesgue measure less than δ;
there exists a Lebesgue integrable function g on the real line such that
For an equivalent definition in terms of functions see the section Relation between the two notions of absolute continuity.
Any other function satisfying (3) is equal to g almost everywhere. Such a function is called Radon-Nikodym derivative, or density, of the absolutely continuous measure μ.
Equivalence between (1), (2) and (3) holds also in Rn for all n=1,2,3,...
Thus, the absolutely continuous measures on Rn are precisely those that have densities; as a special case, the absolutely continuous probability measures are precisely the ones that have probability density function
s.
s on the same measurable space then μ is said to be absolutely continuous with respect to ν, or dominated by ν if μ(A) = 0 for every set A for which ν(A) = 0. This is written as “μ
ν”. In symbols:
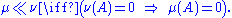
Absolute continuity of measures is reflexive
and transitive
, but is not antisymmetric
, so it is a preorder
rather than a partial order. Instead, if μ
ν and ν 
μ, the measures μ and ν are said to be equivalent
. Thus absolute continuity induces a partial ordering of such equivalence classes.
If μ is a signed
or complex measure
, it is said that μ is absolutely continuous with respect to ν if its variation |μ| satisfies |μ| ≪ ν; equivalently, if every set A for which ν(A) = 0 is μ-null
.
The Radon–Nikodym theorem
states that if μ is absolutely continuous with respect to ν, and both measures are σ-finite, then μ has a density, or "Radon-Nikodym derivative", with respect to ν, which means that there exists a ν-measurable function f taking values in [0, +∞], denoted by f = dμ⁄dν, such that for any ν-measurable set A we have
, every measure can be decomposed into the sum of an absolutely continuous measure and a singular measure. See singular measure
for examples of measures that are not absolutely continuous.
of the real line is absolutely continuous with respect to Lebesgue measure
if and only if the point function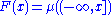
is locally an absolutely continuous real function.
In other words, a function is locally absolutely continuous if and only if its distributional derivative
is a measure that is absolutely continuous with respect to the Lebesgue measure.
If the absolute continuity holds then the Radon-Nikodym derivative of μ is equal almost everywhere to the derivative of F.
More generally, the measure μ is assumed to be locally finite (rather than finite) and F(x) is defined as μ((0,x]) for x>0, 0 for x=0, and -μ((x,0]) for x<0. In this case μ is the Lebesgue-Stieltjes measure generated by F.
The relation between the two notions of absolute continuity still holds.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the relationship between the two central operations of calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, stated by fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
and absolute continuity. For real-valued functions on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
two interrelated notions appear, absolute continuity of functions and absolute continuity of measures. These two notions are generalized in different directions. The usual derivative of a function is related to the Radon–Nikodym derivative, or density, of a measure.
Absolute continuity of functions
It may happen that a continuous function f is differentiable almost everywhere on [0,1], its derivative f ′ is Lebesgue integrable, and nevertheless the integral of f ′ differs from the increment of f. For example, this happens for the Cantor functionCantor function
In mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
, which means that this function is not absolutely continuous. Absolute continuity of functions is a smoothness property which is stricter than continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and uniform continuity
Uniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
.
Definition
Let I be an intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
in the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R. A function f: I → R is absolutely continuous on I if for every positive number
, there is a positive number 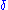such that whenever a finite sequence of pairwise disjoint sub-intervals (xk, yk) of I satisfies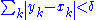then
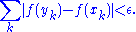
The collection of all absolutely continuous functions on I is denoted AC(I).
Equivalent definitions
The following conditions on a real-valued function f on a compact interval [a,b] are equivalent:f is absolutely continuous;
f has a derivative f ′ almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
, the derivative is Lebesgue integrable, and
-
-
- for all x on [a,b];
there exists a Lebesgue integrable function g on [a,b] such that
-
-
- for all x on [a,b].
If these equivalent conditions are satisfied then necessarily g = f ′ almost everywhere.
Equivalence between (1) and (3) is known as the fundamental theorem of Lebesgue integral calculus, due to Lebesgue.
For an equivalent definition in terms of measures see the section Relation between the two notions of absolute continuity.
Properties
- The sum and difference of two absolutely continuous functions are also absolutely continuous. If the two functions are defined on a bounded closed interval, then their product is also absolutely continuous.
- If an absolutely continuous function is defined on a bounded closed interval and is nowhere zero then its reciprocal is absolutely continuous.
- Every absolutely continuous function is uniformly continuousUniform continuityIn mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
and, therefore, continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Every Lipschitz-continuousLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is absolutely continuous.
- If f: [a,b] → R is absolutely continuous, then it is of bounded variationBounded variationIn mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
on [a,b].
- If f: [a,b] → R is absolutely continuous, then it has the Luzin N propertyLuzin N propertyIn mathematics, a function f on the interval [a, b] has the Luzin N property, named after Nikolai Luzin if for all N\subset[a,b] such that \lambda=0, there holds: \lambda=0, where \lambda stands for the Lebesgue measure.Note that the image of such a set N is not necessarily measurable, but since...
(that is, for any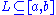
such that 
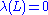, it holds that 
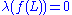, where 
stands for the Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on R).
- f: I → R is absolutely continuous if and only if it is continuous, is of bounded variation and has the Luzin N property.
Examples
The following functions are continuous everywhere but not absolutely continuous:- the Cantor functionCantor functionIn mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
; - the function
-
- on a finite interval containing the origin;
- the function ƒ(x) = x 2 on an unbounded interval.
Generalizations
Let (X, d) be a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
and let I be an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
in the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R. A function f: I → X is absolutely continuous on I if for every positive number
, there is a positive number 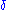such that whenever a finite sequence of pairwise disjoint sub-intervals [xk, yk] of I satisfies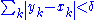then
The collection of all absolutely continuous functions from I into X is denoted AC(I; X).
A further generalization is the space ACp(I; X) of curves f: I → X such that
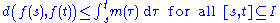
for some m in the Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
Lp(I).
Properties of these generalizations
- Every absolutely continuous function is uniformly continuousUniform continuityIn mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
and, therefore, continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Every Lipschitz-continuousLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is absolutely continuous.
- If f: [a,b] → X is absolutely continuous, then it is of bounded variationBounded variationIn mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
on [a,b].
- For f ∈ ACp(I; X), the metric derivativeMetric derivativeIn mathematics, the metric derivative is a notion of derivative appropriate to parametrized paths in metric spaces. It generalizes the notion of "speed" or "absolute velocity" to spaces which have a notion of distance but not direction .-Definition:Let be a metric space...
of f exists for λ-almost allAlmost allIn mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
times in I, and the metric derivative is the smallest m ∈ Lp(I; R) such that
Definition
A measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
μ on Borel subsets
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
of the real line is absolutely continuous with respect to Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
λ (in other words, dominated by λ) if μ(A) = 0 for every set A for which λ(A) = 0. This is written as “μ << λ”.
In most applications, if a measure on the real line is simply said to be absolutely continuous — without specifying with respect to which other measure it is absolutely continuous — then absolute continuity with respect to Lebesgue measure is meant.
The same holds for Rn for all n=1,2,3,...
Equivalent definitions
The following conditions on a finite measure μ on Borel subsets of the real line are equivalent:μ is absolutely continuous;
for every positive number ε there is a positive number δ such that μ(A) < ε for all Borel sets A of Lebesgue measure less than δ;
there exists a Lebesgue integrable function g on the real line such that
-
-
- for all Borel subsets A of the real line.
For an equivalent definition in terms of functions see the section Relation between the two notions of absolute continuity.
Any other function satisfying (3) is equal to g almost everywhere. Such a function is called Radon-Nikodym derivative, or density, of the absolutely continuous measure μ.
Equivalence between (1), (2) and (3) holds also in Rn for all n=1,2,3,...
Thus, the absolutely continuous measures on Rn are precisely those that have densities; as a special case, the absolutely continuous probability measures are precisely the ones that have probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s.
Generalizations
If μ and ν are two measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
s on the same measurable space then μ is said to be absolutely continuous with respect to ν, or dominated by ν if μ(A) = 0 for every set A for which ν(A) = 0. This is written as “μ
ν”. In symbols: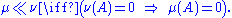Absolute continuity of measures is reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, but is not antisymmetric
Antisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
, so it is a preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
rather than a partial order. Instead, if μ
ν and ν μ, the measures μ and ν are said to be equivalentEquivalence (measure theory)
In mathematics, and specifically in measure theory, equivalence is a notion of two measures being "the same".-Definition:Let be a measurable space, and let μ, ν : Σ → R be two signed measures. Then μ is said to be equivalent to ν if and only if each is absolutely continuous with respect to the other...
. Thus absolute continuity induces a partial ordering of such equivalence classes.
If μ is a signed
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
or complex measure
Complex measure
In mathematics, specifically measure theory, a complex measure generalizes the concept of measure by letting it have complex values. In other words, one allows for sets whose size is a complex number.-Definition:...
, it is said that μ is absolutely continuous with respect to ν if its variation |μ| satisfies |μ| ≪ ν; equivalently, if every set A for which ν(A) = 0 is μ-null
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
.
The Radon–Nikodym theorem
Radon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
states that if μ is absolutely continuous with respect to ν, and both measures are σ-finite, then μ has a density, or "Radon-Nikodym derivative", with respect to ν, which means that there exists a ν-measurable function f taking values in [0, +∞], denoted by f = dμ⁄dν, such that for any ν-measurable set A we have
Singular measures
Via Lebesgue's decomposition theoremLebesgue's decomposition theorem
In mathematics, more precisely in measure theory, Lebesgue's decomposition theorem is a theorem which states that given \mu and \nu two σ-finite signed measures on a measurable space , there exist two σ-finite signed measures \nu_0 and \nu_1 such that:* \nu=\nu_0+\nu_1\, * \nu_0\ll\mu *...
, every measure can be decomposed into the sum of an absolutely continuous measure and a singular measure. See singular measure
Singular measure
In mathematics, two positive measures μ and ν defined on a measurable space are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A...
for examples of measures that are not absolutely continuous.
Relation between the two notions of absolute continuity
A finite measure μ on Borel subsetsBorel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
of the real line is absolutely continuous with respect to Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
if and only if the point function
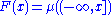
is locally an absolutely continuous real function.
In other words, a function is locally absolutely continuous if and only if its distributional derivative
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
is a measure that is absolutely continuous with respect to the Lebesgue measure.
If the absolute continuity holds then the Radon-Nikodym derivative of μ is equal almost everywhere to the derivative of F.
More generally, the measure μ is assumed to be locally finite (rather than finite) and F(x) is defined as μ((0,x]) for x>0, 0 for x=0, and -μ((x,0]) for x<0. In this case μ is the Lebesgue-Stieltjes measure generated by F.
The relation between the two notions of absolute continuity still holds.