Genus of a multiplicative sequence
Encyclopedia
In mathematics
, the genus of a multiplicative sequence is a ring homomorphism
, from the cobordism ring
of smooth oriented compact manifolds to another ring
, usually the ring of rational number
s.
The manifolds may have some extra structure; for example, they might be oriented, or spin, and so on (see list of cobordism theories for many more examples). The value φ(X) is in some ring, often the ring of rational numbers, though it can be other rings such as Z/2Z or the ring of modular forms.
The conditions on φ can be rephrased as saying that φ is a ring homomorphism from the cobordism ring of manifolds (with given structure) to another ring.
Example: If φ(X) is the signature
of the oriented manifold X, then φ is a genus from oriented manifolds to the ring of integers.
implies that
If Q(z) is a formal power series
in z with constant term 1, we can define a multiplicative sequence
by
where pk is the kth elementary symmetric function of the indeterminates zi. (The variables pk will often in practice be Pontryagin class
es.)
The genus φ of oriented manifolds corresponding to Q is given by
where the pk are the Pontryagin class
es of X.
The power series Q is called the characteristic power series of the genus φ. Thom's theorem states that the rationals tensored with the cobordism ring is a polynomial algebra in generators of degree 4k for positive integers k implies that this gives a bijection between formal power series Q with rational coefficients and leading coefficient 1, and genera from oriented manifolds to the rational numbers.
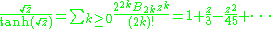
where the numbers B2k are the Bernoulli number
s.
The first few values are
Now let M be a closed smooth oriented manifold of dimension 4n with Pontrjagin classes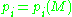
. Friedrich Hirzebruch
showed that the L genus of M in dimension 4n evaluated on the fundamental class
of M,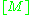
, is equal to 
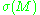, the signature
of M (i.e. the signature of the intersection form on the 2nth cohomology group of M ):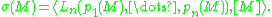
This is now known as the Hirzebruch signature theorem
(or sometimes the Hirzebruch index theorem). René Thom
had earlier proved that the signature was given by some linear combination of Pontryagin numbers, and Hirzebruch found the exact formula for this linear combination given above.
The fact that L2 is always integral for a smooth manifold was used by John Milnor
to give an example of an 8-dimensional PL manifold with no smooth structure
. Pontryagin numbers can also be defined for PL manifolds, and Milnor showed that his PL manifold had a non-integral value of p2, and so was not smoothable.
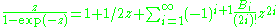
with B2k as before, Bernoulli numbers.
The first few values are
The Todd genus has the particular property that it assigns the value 1 to all complex projective spaces (i.e.
), and this suffices to show that the Todd genus agrees with the arithmetic genus for algebraic varieties as the arithmetic genus is also 1 for complex projective spaces. This observation is a consequence of the Hirzebruch–Riemann–Roch theorem, and in fact was one of the key developments that led to the formulation of that theorem.
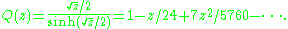
(There is also an  genus which is less commonly used, associated to the characteristic series Q(16z).) The first few values are
The  genus of a spin manifold is an integer, and an even integer if the dimension is 4 mod 8 (which in dimension 4 implies Rochlin's theorem) – for general manifolds, the  genus is not always an integer. This was proven by Hirzebruch
and Borel
; this result both motivated and was later explained by the Atiyah–Singer index theorem
, which showed that the  genus of a spin manifold is equal to the index of its Dirac operator
.
By combining this index result with a Weitzenbock formula for the Dirac Laplacian,
Lichnerowicz deduced that if a compact spin manifold admits a metric with positive scalar curvature, its  genus must vanish.
This only gives an obstruction to positive scalar curvaure when the dimension is a multiple of 4, but
Hitchin later discovered an analogous
-valued obstruction in dimensions 1 or 2 mod 8. These results are essentially sharp.
Indeed, Gromov, Lawson, and Stolz later proved that the  genus and Hitchin's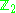
-valued analog are the only obstructions to the existence of
positive-scalar-curvature metrics on simply-connected spin manifolds of dimension greater than or equal to 5.
for constants δ and ε. (As usual, Q is the characteristic power series of the genus.)
Examples:
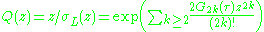
where σL is the Weierstrass sigma function
for the lattice L, and G is a multiple of an Eisenstein series
.
The Witten genus of a 4k dimensional compact oriented smooth spin manifold with vanishing first Pontryagin class is a modular form
of weight 2k, with integral Fourier coefficients.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the genus of a multiplicative sequence is a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
, from the cobordism ring
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
of smooth oriented compact manifolds to another ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, usually the ring of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s.
Definition
A genus φ assigns a number φ(X) to each manifold X such that- φ(X∪Y) = φ(X) + φ(Y) (where ∪ is the disjoint union)
- φ(X×Y) = φ(X)φ(Y)
- φ(X) = 0 if X is a boundary.
The manifolds may have some extra structure; for example, they might be oriented, or spin, and so on (see list of cobordism theories for many more examples). The value φ(X) is in some ring, often the ring of rational numbers, though it can be other rings such as Z/2Z or the ring of modular forms.
The conditions on φ can be rephrased as saying that φ is a ring homomorphism from the cobordism ring of manifolds (with given structure) to another ring.
Example: If φ(X) is the signature
Signature (topology)
In the mathematical field of topology, the signature is an integer invariant which is defined for an oriented manifold M of dimension d=4k divisible by four ....
of the oriented manifold X, then φ is a genus from oriented manifolds to the ring of integers.
The genus of a formal power series
A sequence of polynomials K1, K2,... in variables p1,p2,... is called multiplicative if- 1 + p1z + p2z2 + ... = (1 + q1z + q2z2 + ...) (1 + r1z + r2z2 + ...)
implies that
- ΣKj(p1,p2,...)zj = ΣKj(q1,q2,...)zjΣKk(r1,r2,...)zk
If Q(z) is a formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
in z with constant term 1, we can define a multiplicative sequence
- K = 1+ K1 + K2 + ...
by
- K(p1,p2,p3,...) = Q(z1)Q(z2)Q(z3)...
where pk is the kth elementary symmetric function of the indeterminates zi. (The variables pk will often in practice be Pontryagin class
Pontryagin class
In mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
es.)
The genus φ of oriented manifolds corresponding to Q is given by
- φ(X) = K(p1,p2,p3,...)
where the pk are the Pontryagin class
Pontryagin class
In mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
es of X.
The power series Q is called the characteristic power series of the genus φ. Thom's theorem states that the rationals tensored with the cobordism ring is a polynomial algebra in generators of degree 4k for positive integers k implies that this gives a bijection between formal power series Q with rational coefficients and leading coefficient 1, and genera from oriented manifolds to the rational numbers.
L genus and the Hirzebruch signature theorem
The L genus is the genus of the formal power series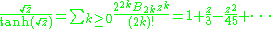where the numbers B2k are the Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s.
The first few values are
- L0 = 1
- L1 = p1/3
- L2 = (7p2 − p12)/45.
Now let M be a closed smooth oriented manifold of dimension 4n with Pontrjagin classes
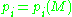. Friedrich HirzebruchFriedrich Hirzebruch
Friedrich Ernst Peter Hirzebruch is a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation.-Life:He was born in Hamm, Westphalia...
showed that the L genus of M in dimension 4n evaluated on the fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
of M,
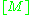, is equal to 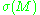, the signatureSignature (topology)
In the mathematical field of topology, the signature is an integer invariant which is defined for an oriented manifold M of dimension d=4k divisible by four ....
of M (i.e. the signature of the intersection form on the 2nth cohomology group of M ):
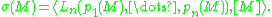
This is now known as the Hirzebruch signature theorem
(or sometimes the Hirzebruch index theorem). René Thom
René Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
had earlier proved that the signature was given by some linear combination of Pontryagin numbers, and Hirzebruch found the exact formula for this linear combination given above.
The fact that L2 is always integral for a smooth manifold was used by John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
to give an example of an 8-dimensional PL manifold with no smooth structure
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
. Pontryagin numbers can also be defined for PL manifolds, and Milnor showed that his PL manifold had a non-integral value of p2, and so was not smoothable.
Todd genus
The Todd genus is the genus of the formal power series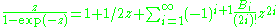with B2k as before, Bernoulli numbers.
The first few values are
- Td0 = 1
- Td1 = c1/2
- Td2 = (c2 + c12)/12.
- Td3 = (c1c2)/24.
- Td4 = (-c14 + 4 c2c12+3c22+c3c1-c4)/720.
The Todd genus has the particular property that it assigns the value 1 to all complex projective spaces (i.e.
), and this suffices to show that the Todd genus agrees with the arithmetic genus for algebraic varieties as the arithmetic genus is also 1 for complex projective spaces. This observation is a consequence of the Hirzebruch–Riemann–Roch theorem, and in fact was one of the key developments that led to the formulation of that theorem. genus
The  genus is the genus associated to the characteristic power series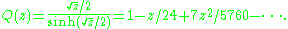(There is also an  genus which is less commonly used, associated to the characteristic series Q(16z).) The first few values are
- Â0 = 1
- Â1 = −p1/24
- Â2 = (−4p2 + 7 p12)/5760.
The  genus of a spin manifold is an integer, and an even integer if the dimension is 4 mod 8 (which in dimension 4 implies Rochlin's theorem) – for general manifolds, the  genus is not always an integer. This was proven by Hirzebruch
Friedrich Hirzebruch
Friedrich Ernst Peter Hirzebruch is a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation.-Life:He was born in Hamm, Westphalia...
and Borel
Armand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
; this result both motivated and was later explained by the Atiyah–Singer index theorem
Atiyah–Singer index theorem
In differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index...
, which showed that the  genus of a spin manifold is equal to the index of its Dirac operator
Dirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
.
By combining this index result with a Weitzenbock formula for the Dirac Laplacian,
Lichnerowicz deduced that if a compact spin manifold admits a metric with positive scalar curvature, its  genus must vanish.
This only gives an obstruction to positive scalar curvaure when the dimension is a multiple of 4, but
Hitchin later discovered an analogous
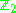-valued obstruction in dimensions 1 or 2 mod 8. These results are essentially sharp.Indeed, Gromov, Lawson, and Stolz later proved that the  genus and Hitchin's
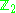-valued analog are the only obstructions to the existence ofpositive-scalar-curvature metrics on simply-connected spin manifolds of dimension greater than or equal to 5.
Elliptic genus
A genus is called an elliptic genus if the power series Q(z) = z/f(z) satisfies the condition- f ′2 = 1 − 2δf2 + εf4
for constants δ and ε. (As usual, Q is the characteristic power series of the genus.)
Examples:
- δ = ε = 1, f(z) = tanh(z). This is the L-genus.
- δ = −1/8, ε = 0, f(z) = 2sinh(z/2). This is the  genus.
Witten genus
The Witten genus is the genus associated to the characteristic power series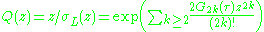where σL is the Weierstrass sigma function
Weierstrass sigma function
In mathematics, the Weierstrass functions are special functions of a complex variable that are auxiliary to the Weierstrass elliptic function. They are named for Karl Weierstrass.-Weierstrass sigma-function:...
for the lattice L, and G is a multiple of an Eisenstein series
Eisenstein series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
.
The Witten genus of a 4k dimensional compact oriented smooth spin manifold with vanishing first Pontryagin class is a modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
of weight 2k, with integral Fourier coefficients.