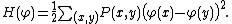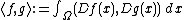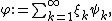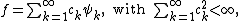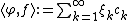Gaussian free field
Encyclopedia
In probability theory
and statistical mechanics
, the Gaussian free field (GFF) is a Gaussian random field
, a central model of random surfaces (random height functions). A nice survey is .
The discrete version can be defined on any graph
, usually a lattice in d-dimensional Euclidean space. The continuum version is defined on Rd or on a bounded domain of that. It can be thought of as the natural generalization of one-dimensional Brownian motion
to d time (but still one space) dimensions; in particular, the one-dimensional continuum GFF is just the standard one-dimensional Brownian motion or Brownian bridge
on an interval.
In the theory of random surfaces, it is also called the harmonic crystal. It is also the starting point for many constructions in quantum field theory
, where it is called the Euclidean bosonic
massless free field. A key property of the 2-dimensional GFF is conformal invariance
, which relates it in several ways to the Schramm-Loewner Evolution, see and .
Similarly to Brownian motion, which is the scaling limit
of a wide range of discrete random walk
models (see Donsker's theorem
), the continuum GFF is the scaling limit of not only the discrete GFF on lattices, but of many random height function models, such as the height function of uniform random planar domino tiling
s, see . The planar GFF is also the limit of the fluctuations of the characteristic polynomial
of a random matrix
model, the Ginibre ensemble, see .
given by a random walk
on a finite graph G(V, E). Let U be a fixed non-empty subset of the vertices V, and take the set of all real-valued functions φ with some prescribed values on U. We then define a Hamiltonian
by
Then, the random function with probability density
proportional to exp(−H(φ)) with respect to the Lebesgue measure
on RV−U is called the discrete GFF with boundary U.
It is not hard to show that the expected value
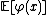is exactly the discrete harmonic
extension of the boundary values from U (harmonic with respect to the transition kernel P), and the covariance
s Cov[φ(x), φ(y)] are equal to the discrete Green's function
G(x, y).
So, in one sentence, the GFF is the Gaussian random field
on V with covariance structure given by the Green's function associated to the transition kernel P.
on distribution
s (with two different meanings of the word "distribution").
Given a domain Ω ⊆ Rn, consider the Dirichlet inner product
for smooth functions ƒ and g on Ω, coinciding with some prescribed boundary function on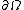
, where 
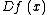is the gradient vector at 
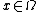. Then take the Hilbert space
closure with respect to this inner product, this is the Sobolev space
.
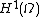The continuum GFF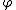
on 
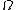is a Gaussian random field
indexed by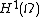
, i.e., a collection of Gaussian random variables, one for each 
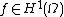, denoted by 
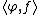, such that the covariance
structure is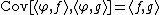
for all 
.
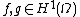Such a random field indeed exists, and its distribution is unique. Given any orthonormal basis
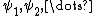of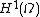 
(with the given boundary condition), we can form the formal infinite sum
where the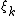
are i.i.d. standard normal variables. This random sum almost surely will not exist as an element of 
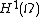, since its variance
is infinite. However, it exists as a random generalized function
, since for any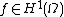
we have
hence
is a well-defined finite random number.
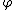does not exist as a random element of 
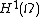, it still could be that it is a random function on 
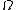in some larger function space. In fact, in dimension 
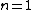, an orthonormal basis of 
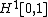is given by
and then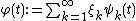
is easily seen to be a one-dimensional Brownian motion (or Brownian bridge, if the boundary values for 
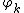are set up that way). So, in this case, it is a random continuous function. For instance, if 
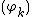is the Haar basis, then this is Lévy's construction of Brownian motion, see, e.g., Section 3 of .
On the other hand, for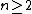
it can indeed be shown to exist only as a generalized function, see .
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the Gaussian free field (GFF) is a Gaussian random field
Gaussian random field
A Gaussian random field is a random field involving Gaussian probability density functions of the variables. A one-dimensional GRF is also called a Gaussian process....
, a central model of random surfaces (random height functions). A nice survey is .
The discrete version can be defined on any graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, usually a lattice in d-dimensional Euclidean space. The continuum version is defined on Rd or on a bounded domain of that. It can be thought of as the natural generalization of one-dimensional Brownian motion
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
to d time (but still one space) dimensions; in particular, the one-dimensional continuum GFF is just the standard one-dimensional Brownian motion or Brownian bridge
Brownian bridge
A Brownian bridge is a continuous-time stochastic process B whose probability distribution is the conditional probability distribution of a Wiener process W given the condition that B = B = 0.The expected value of the bridge is zero, with variance t, implying that the most...
on an interval.
In the theory of random surfaces, it is also called the harmonic crystal. It is also the starting point for many constructions in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, where it is called the Euclidean bosonic
Bosonic field
In quantum field theory, a bosonic field is a quantum field whose quanta are bosons; that is, they obey Bose-Einstein statistics. Bosonic fields obey canonical commutation relations, as distinct from the canonical anticommutation relations obeyed by fermionic fields.Examples include scalar fields,...
massless free field. A key property of the 2-dimensional GFF is conformal invariance
Conformal group
In mathematics, the conformal group is the group of transformations from a space to itself that preserve all angles within the space. More formally, it is the group of transformations that preserve the conformal geometry of the space. Several specific conformal groups are particularly important:*...
, which relates it in several ways to the Schramm-Loewner Evolution, see and .
Similarly to Brownian motion, which is the scaling limit
Scaling limit
In physics or mathematics, the scaling limit is a term applied to the behaviour of a lattice model in the limit of the lattice spacing going to zero. A lattice model which approximates a continuum quantum field theory in the limit as the lattice spacing goes to zero corresponds to finding a second...
of a wide range of discrete random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
models (see Donsker's theorem
Donsker's theorem
In probability theory, Donsker's theorem, named after M. D. Donsker, identifies a certain stochastic process as a limit of empirical processes. It is sometimes called the functional central limit theorem....
), the continuum GFF is the scaling limit of not only the discrete GFF on lattices, but of many random height function models, such as the height function of uniform random planar domino tiling
Domino tiling
A domino tiling of a region in the Euclidean plane is a tessellation of the region by dominos, shapes formed by the union of two unit squares meeting edge-to-edge...
s, see . The planar GFF is also the limit of the fluctuations of the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of a random matrix
Random matrix
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...
model, the Ginibre ensemble, see .
Definition of the discrete GFF
Let P(x, y) be the transition kernel of the Markov chainMarkov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
given by a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
on a finite graph G(V, E). Let U be a fixed non-empty subset of the vertices V, and take the set of all real-valued functions φ with some prescribed values on U. We then define a Hamiltonian
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
by
Then, the random function with probability density
Probability density
Probability density may refer to:* Probability density function in probability theory* The product of the probability amplitude with its complex conjugate in quantum mechanics...
proportional to exp(−H(φ)) with respect to the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on RV−U is called the discrete GFF with boundary U.
It is not hard to show that the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
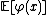is exactly the discrete harmonicHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
extension of the boundary values from U (harmonic with respect to the transition kernel P), and the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
s Cov[φ(x), φ(y)] are equal to the discrete Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
G(x, y).
So, in one sentence, the GFF is the Gaussian random field
Gaussian random field
A Gaussian random field is a random field involving Gaussian probability density functions of the variables. A one-dimensional GRF is also called a Gaussian process....
on V with covariance structure given by the Green's function associated to the transition kernel P.
The continuum field
The definition of the continuum field necessarily uses some abstract machinery, since it does not exist as a random height function. Instead, it is a random generalized function, or in other words, a distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s (with two different meanings of the word "distribution").
Given a domain Ω ⊆ Rn, consider the Dirichlet inner product
Dirichlet energy
In mathematics, the Dirichlet's energy is a numerical measure of how variable a function is. More abstractly, it is a quadratic functional on the Sobolev space...
for smooth functions ƒ and g on Ω, coinciding with some prescribed boundary function on
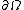, where 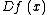is the gradient vector at 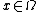. Then take the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
closure with respect to this inner product, this is the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
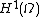.The continuum GFF
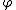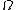on is a Gaussian random fieldGaussian random field
A Gaussian random field is a random field involving Gaussian probability density functions of the variables. A one-dimensional GRF is also called a Gaussian process....
indexed by
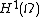, i.e., a collection of Gaussian random variables, one for each 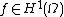, denoted by 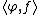, such that the covarianceCovariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
structure is
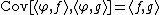for all 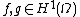.Such a random field indeed exists, and its distribution is unique. Given any orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
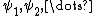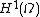of (with the given boundary condition), we can form the formal infinite sum
where the
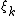are i.i.d. standard normal variables. This random sum almost surely will not exist as an element of 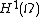, since its varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
is infinite. However, it exists as a random generalized function
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
, since for any
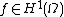we have
hence
is a well-defined finite random number.
Special case: n = 1
Although the above argument shows that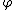 does not exist as a random element of 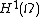, it still could be that it is a random function on 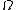in some larger function space. In fact, in dimension 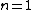, an orthonormal basis of 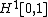is given by-
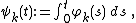where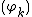 
form an orthonormal basis of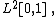 
and then
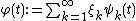is easily seen to be a one-dimensional Brownian motion (or Brownian bridge, if the boundary values for 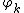are set up that way). So, in this case, it is a random continuous function. For instance, if 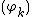is the Haar basis, then this is Lévy's construction of Brownian motion, see, e.g., Section 3 of .On the other hand, for
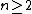it can indeed be shown to exist only as a generalized function, see .