
Essential spectrum
Encyclopedia
In mathematics
, the essential spectrum of a bounded operator
is a certain subset of its spectrum
, defined by a condition of the type that says, roughly speaking, "fails badly to be invertible".
and let T be a bounded
self-adjoint
operator on X.
s λ such that
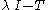
is not a Fredholm operator
.
Here, an operator is Fredholm if its range
is closed and its kernel
and cokernel
are finite-dimensional. Furthermore, I denotes the identity operator on X, so that I(x) = x for all x in X.
, and it is a subset of the spectrum
. Since T is self-adjoint, the spectrum is contained on the real axis.
The essential spectrum is invariant under compact perturbations. That is, if K is a compact operator
on X, then the essential spectra of T and that of T + K coincide. This explains why it is called the essential spectrum: Weyl
(1910) originally defined the essential spectrum of a certain differential operator to be the spectrum independent of boundary conditions.
Weyl's criterion for the essential spectrum is as follows. First, a number λ is in the spectrum of T if and only if there exists a sequence
{ψk} in the space X such that ||ψk|| = 1 and
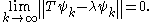
Furthermore, λ is in the essential spectrum if there is a sequence satisfying this condition, but such that it contains no convergent subsequence
(this is the case if, for example is an orthonormal sequence); such a sequence is called a singular sequence.
is an orthonormal sequence); such a sequence is called a singular sequence.
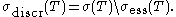
A number λ is in the discrete spectrum if it is an isolated eigenvalue of finite multiplicity, meaning that the dimension of the space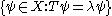
is finite but non-zero and that there is an ε > 0 such that μ ∈ σ(T) and |μ−λ| < ε imply that μ and λ are equal.
and T is a bounded operator on X. There are several definitions of the essential spectrum in the literature, which are not equivalent.
The essential spectrum of an operator is closed, whatever definition is used. Furthermore,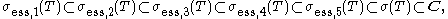
but any of these inclusions may be strict. However, for self-adjoint operators, all the above definitions for the essential spectrum coincide.
Define the radius of the essential spectrum by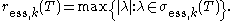
Even though the spectra may be different, the radius is the same for all k.
The essential spectrum σess,k(T) is invariant under compact perturbations for k = 1,2,3,4, but not for k = 5. The case k = 4 gives the part of the spectrum that is independent of compact perturbations, that is,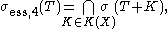
where K(X) denotes the set of compact operators on X.
The second definition generalizes Weyl's criterion: σess,2(T) is the set of all λ for which there is no singular sequence.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the essential spectrum of a bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
is a certain subset of its spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
, defined by a condition of the type that says, roughly speaking, "fails badly to be invertible".
The essential spectrum of self-adjoint operators
In formal terms, let X be a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and let T be a bounded
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
self-adjoint
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
operator on X.
Definition
The essential spectrum of T, usually denoted σess(T), is the set of all complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s λ such that
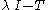
is not a Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
.
Here, an operator is Fredholm if its range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
is closed and its kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
and cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
are finite-dimensional. Furthermore, I denotes the identity operator on X, so that I(x) = x for all x in X.
Properties
The essential spectrum is always closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
, and it is a subset of the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
. Since T is self-adjoint, the spectrum is contained on the real axis.
The essential spectrum is invariant under compact perturbations. That is, if K is a compact operator
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
on X, then the essential spectra of T and that of T + K coincide. This explains why it is called the essential spectrum: Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
(1910) originally defined the essential spectrum of a certain differential operator to be the spectrum independent of boundary conditions.
Weyl's criterion for the essential spectrum is as follows. First, a number λ is in the spectrum of T if and only if there exists a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
{ψk} in the space X such that ||ψk|| = 1 and
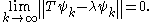
Furthermore, λ is in the essential spectrum if there is a sequence satisfying this condition, but such that it contains no convergent subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
(this is the case if, for example
 is an orthonormal sequence); such a sequence is called a singular sequence.
is an orthonormal sequence); such a sequence is called a singular sequence.The discrete spectrum
The essential spectrum is a subset of the spectrum σ, and its complement is called the discrete spectrum, so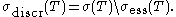
A number λ is in the discrete spectrum if it is an isolated eigenvalue of finite multiplicity, meaning that the dimension of the space
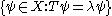
is finite but non-zero and that there is an ε > 0 such that μ ∈ σ(T) and |μ−λ| < ε imply that μ and λ are equal.
The essential spectrum of general bounded operators
In the general case, X denotes a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and T is a bounded operator on X. There are several definitions of the essential spectrum in the literature, which are not equivalent.
- The essential spectrum σess,1(T) is the set of all λ such that λI − T is not semi-Fredholm (an operator is semi-Fredholm if its range is closed and its kernel or its cokernel is finite-dimensional).
- The essential spectrum σess,2(T) is the set of all λ such that the range of λI − T is not closed or the kernel of λI − T is infinite-dimensional.
- The essential spectrum σess,3(T) is the set of all λ such that λI − T is not Fredholm (an operator is Fredholm if its range is closed and both its kernel and its cokernel are finite-dimensional).
- The essential spectrum σess,4(T) is the set of all λ such that λI − T is not Fredholm with index zero (the index of a Fredholm operator is the difference between the dimension of the kernel and the dimension of the cokernel).
- The essential spectrum σess,5(T) is the union of σess,1(T) with all components of C \ σess,1(T) that do not intersect with the resolvent set C \ σ(T).
The essential spectrum of an operator is closed, whatever definition is used. Furthermore,
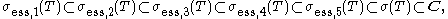
but any of these inclusions may be strict. However, for self-adjoint operators, all the above definitions for the essential spectrum coincide.
Define the radius of the essential spectrum by
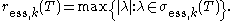
Even though the spectra may be different, the radius is the same for all k.
The essential spectrum σess,k(T) is invariant under compact perturbations for k = 1,2,3,4, but not for k = 5. The case k = 4 gives the part of the spectrum that is independent of compact perturbations, that is,
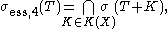
where K(X) denotes the set of compact operators on X.
The second definition generalizes Weyl's criterion: σess,2(T) is the set of all λ for which there is no singular sequence.

