Energy minimization
Encyclopedia
In computational chemistry
, energy minimization (also called energy optimization or geometry optimization) methods are used to compute the equilibrium configuration of molecules and solids.
Stable states of molecular systems correspond to global and local minima on their potential energy surface
. Starting from a non-equilbrium molecular geometry, energy minimization employs the mathematical procedure of optimization
to move atoms so as to reduce the net forces (the gradients of potential energy
) on the atoms until they become negligible.
Like molecular dynamics
and Monte-Carlo
approaches, periodic boundary conditions
have been allowed in energy minimization methods, to make small systems. A well established algorithm of energy minimization can be an efficient tool for molecular structure optimization.
Unlike molecular dynamics
simulations, which are based on Newtonian dynamic laws
and allow calculation of atomic trajectories with kinetic energy
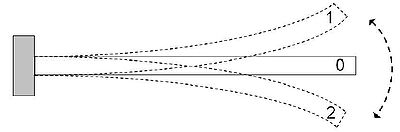
, molecular energy minimization does not include the effect of temperature, and hence the trajectories of atoms during the calculation do not really make any physical sense, i.e. we can only obtain a final state of system that corresponds to a local minimum of potential energy. From a physical point of view, this final state of the system corresponds to the configuration of atoms when the temperature of the system is approximately zero, e.g. as shown in Figure 1, if there is a cantilevered beam
vibrating between positions 1 and 2 around an equilibrium position 0 with an initial kinetic motion
, whether we start with the state 1, the state 2 or any other state between these two positions, the result of energy minimization for this system will always be the state 0.
Gradient-based algorithms are the most popular methods for energy minimization. The basic idea of gradient methods is to move atoms according to the total net forces acting on them. The force on an atom is calculated as the negative gradient of total potential energy of system, as follows:
where ri is the position of atom i and Utot is the total potential energy of the system.
An analytical formula
of the gradient of potential energy is preferentially required by the gradient methods. If not, one needs to calculate numerically the derivative
s of the energy function. In this case, the Powell's direction set method or the downhill simplex method can generally be more efficient than the gradient methods.
, which are the 3 components of the coordinates of N atoms in our system. We calculate the net force on each atom F at each iteration
step t, and we move the atoms in the direction of F with a multiple factor k. k can be smaller at the beginning of calculation if we begin with a very high potential energy
. Note that similar strategy can be used in molecular dynamics
for reducing the probability of divergence
problems at the beginning of simulations.
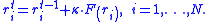
We repeat this step in the above equation t = 1,2,... until F reaches to zero for every atom. The potential energy of system goes down in a long narrow valley of energy in this procedure.
Though it is also called “steepest descent”, the simple gradient algorithm
is in fact very time-consuming if we compare it to the nonlinear conjugate gradient
approach, it is therefore known as a not very good algorithm. However, its advantage is its numerical stability
, i.e., the potential energy can never increase if we take a reasonable k. Thus, it can be combined with a conjugated gradient algorithm for solving the numerical divergence problem when two atoms are too close to each other.
.
In this algorithm, we minimize the energy function by moving the atoms as follows,
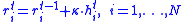
where
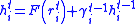
and gamma is updated using the Fletcher-Reeves formula as:
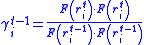
Here we note that gamma can also be calculated by using the Polak-Ribiere formula, however, it is less efficient than the Fletcher-Reeves one for certain energy functions. At the beginning of calculation (when t = 1), we can make the search direction vector h0 = 0.
This algorithm is very efficient. However, it is not quiet stable with certain potential functions, i.e. it sometimes can step so far into a very strong repulsive energy
range (e.g. when two atoms are too close to each other), where the gradient
at this point is almost infinite. It can directly result a typical data-overrun
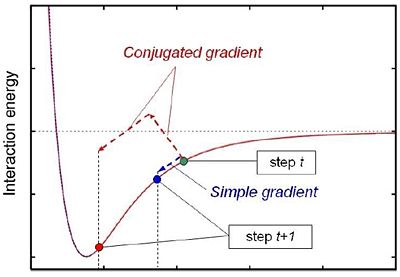
error during the calculation. For resolving this problem, we can combine the conjugate gradient algorithm with the simple one. Figure 3 shows the schematics of this combined predicting algorithm. We note for implementation that steps 2 and 5 can be combined to one single step.
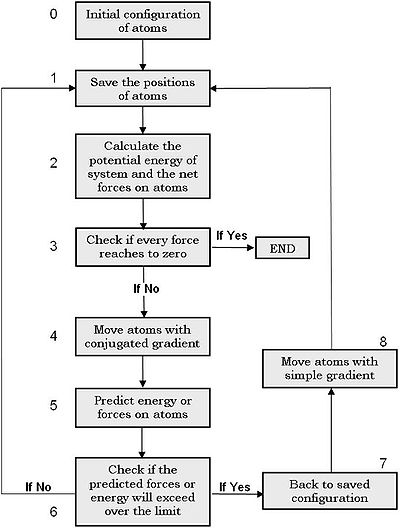
Moreover, one can equally adding other boundary conditions to the minimized energy function, such as adding external forces or external electric fields to the system. In these cases, the terms in potential energy function will be changed but the number of variables remains constant.
Here an example of the application of the energy minimization method in molecular modeling in nanoscience is shown in Figure 4.
Further information about the application of this method in nanoscience and Computational Codes programmed in Fortran
for students is available in the following external links.
Computational chemistry
Computational chemistry is a branch of chemistry that uses principles of computer science to assist in solving chemical problems. It uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids...
, energy minimization (also called energy optimization or geometry optimization) methods are used to compute the equilibrium configuration of molecules and solids.
Stable states of molecular systems correspond to global and local minima on their potential energy surface
Potential energy surface
A potential energy surface is generally used within the adiabatic or Born–Oppenheimer approximation in quantum mechanics and statistical mechanics to model chemical reactions and interactions in simple chemical and physical systems...
. Starting from a non-equilbrium molecular geometry, energy minimization employs the mathematical procedure of optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
to move atoms so as to reduce the net forces (the gradients of potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
) on the atoms until they become negligible.
Like molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
and Monte-Carlo
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
approaches, periodic boundary conditions
Periodic boundary conditions
In mathematical models and computer simulations, periodic boundary conditions are a set of boundary conditions that are often used to simulate a large system by modelling a small part that is far from its edge...
have been allowed in energy minimization methods, to make small systems. A well established algorithm of energy minimization can be an efficient tool for molecular structure optimization.
Unlike molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
simulations, which are based on Newtonian dynamic laws
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
and allow calculation of atomic trajectories with kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
, molecular energy minimization does not include the effect of temperature, and hence the trajectories of atoms during the calculation do not really make any physical sense, i.e. we can only obtain a final state of system that corresponds to a local minimum of potential energy. From a physical point of view, this final state of the system corresponds to the configuration of atoms when the temperature of the system is approximately zero, e.g. as shown in Figure 1, if there is a cantilevered beam
Cantilever
A cantilever is a beam anchored at only one end. The beam carries the load to the support where it is resisted by moment and shear stress. Cantilever construction allows for overhanging structures without external bracing. Cantilevers can also be constructed with trusses or slabs.This is in...
vibrating between positions 1 and 2 around an equilibrium position 0 with an initial kinetic motion
Thermodynamic temperature
Thermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
, whether we start with the state 1, the state 2 or any other state between these two positions, the result of energy minimization for this system will always be the state 0.
where ri is the position of atom i and Utot is the total potential energy of the system.
An analytical formula
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
of the gradient of potential energy is preferentially required by the gradient methods. If not, one needs to calculate numerically the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of the energy function. In this case, the Powell's direction set method or the downhill simplex method can generally be more efficient than the gradient methods.
Simple gradient method
Here we have a single function of the potential energy to minimize with 3N independent variablesVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, which are the 3 components of the coordinates of N atoms in our system. We calculate the net force on each atom F at each iteration
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
step t, and we move the atoms in the direction of F with a multiple factor k. k can be smaller at the beginning of calculation if we begin with a very high potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
. Note that similar strategy can be used in molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
for reducing the probability of divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
problems at the beginning of simulations.
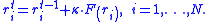
We repeat this step in the above equation t = 1,2,... until F reaches to zero for every atom. The potential energy of system goes down in a long narrow valley of energy in this procedure.
Though it is also called “steepest descent”, the simple gradient algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is in fact very time-consuming if we compare it to the nonlinear conjugate gradient
Nonlinear conjugate gradient method
In numerical optimization, the nonlinear conjugate gradient method generalizes the conjugate gradient method to nonlinear optimization. For a quadratic function \displaystyle f:The minimum of f is obtained when the gradient is 0:...
approach, it is therefore known as a not very good algorithm. However, its advantage is its numerical stability
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
, i.e., the potential energy can never increase if we take a reasonable k. Thus, it can be combined with a conjugated gradient algorithm for solving the numerical divergence problem when two atoms are too close to each other.
Nonlinear conjugate gradient method
The conjugate gradient algorithm includes two basic steps: adding an orthogonal vector to the current direction of the search, and then move them in another direction nearly perpendicular to this vector. These two steps are also known as: step on the valley floor and then jump down. Figure 2 shows a highly simplified comparison between the conjugate and the simple gradient methods on a 1D energy curvePotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
.
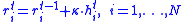
where
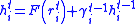
and gamma is updated using the Fletcher-Reeves formula as:
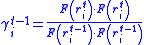
Here we note that gamma can also be calculated by using the Polak-Ribiere formula, however, it is less efficient than the Fletcher-Reeves one for certain energy functions. At the beginning of calculation (when t = 1), we can make the search direction vector h0 = 0.
This algorithm is very efficient. However, it is not quiet stable with certain potential functions, i.e. it sometimes can step so far into a very strong repulsive energy
Van der Waals force
In physical chemistry, the van der Waals force , named after Dutch scientist Johannes Diderik van der Waals, is the sum of the attractive or repulsive forces between molecules other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral...
range (e.g. when two atoms are too close to each other), where the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
at this point is almost infinite. It can directly result a typical data-overrun
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
error during the calculation. For resolving this problem, we can combine the conjugate gradient algorithm with the simple one. Figure 3 shows the schematics of this combined predicting algorithm. We note for implementation that steps 2 and 5 can be combined to one single step.
Boundary conditions
The atoms in our system can have different degrees of freedom. For example, in case of a tube suspended over two supports, we need to fix certain number of atoms N* at the tube ends during the calculation. In this case, it is enough not to move these N* atoms in the step 4 or 8 in Figure 3, but we still calculate their interaction with other atoms in the steps 2 and 5. i.e. from mathematical point of view, we change the total number of variables in the energy function from 3N to 3N-3N*using the boundary condition, by which the values of these 3N* unknown variables are taken as known constants. Note that one can even fix atoms in only one or two directions in this way.Moreover, one can equally adding other boundary conditions to the minimized energy function, such as adding external forces or external electric fields to the system. In these cases, the terms in potential energy function will be changed but the number of variables remains constant.
Here an example of the application of the energy minimization method in molecular modeling in nanoscience is shown in Figure 4.
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
for students is available in the following external links.
See also
- Graph cuts in computer visionGraph cuts in computer visionAs applied in the field of computer vision, graph cuts can be employed to efficiently solve a wide variety of low-level computer vision problems , such as image smoothing, the stereo correspondence problem, and many other computer vision problems that can be formulated in terms of energy minimization...
– apparatus for solving computer visionComputer visionComputer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
problems that can be formulated in terms of energy minimization - Energy principles in structural mechanicsEnergy principles in structural mechanicsEnergy principles in structural mechanics express the relationships between stresses, strains or deformations, displacements, material properties, and external effects in the form of energy or work done by internal and external forces...
Additional references
- Payne et al., "Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients", Reviews of Modern Physics 64 (4), pp. 1045–1097. (1992) (abstract)
- Atich et al., "Conjugate gradient minimization of the energy functional: A new method for electronic structure calculation", Physical Review B 39 (8), pp. 4997–5004, (1989)
- Chadi, "Energy-minimization approach to the atomic geometry of semiconductor surfaces", Physical Review Letters 41 (15), pp. 1062–1065 (1978)