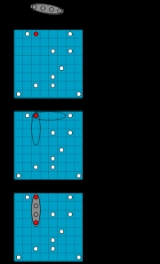
Monte Carlo methods are a class of computation

Computation

Computation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...

al algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

s that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulation

Computer simulation

A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...

s of physical

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

 and mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 systems. These methods are most suited to calculation by a computer

Computer

A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...

 and tend to be used when it is infeasible to compute an exact result with a deterministic algorithm

Deterministic algorithm

In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...

. This method is also used to complement the theoretical derivations.

Monte Carlo methods are especially useful for simulating systems with many coupled

Coupling (physics)

In physics, two systems are coupled if they are interacting with each other. Of special interest is the coupling of two vibratory systems by means of springs or magnetic fields, etc...

 degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model

Cellular Potts model

The cellular Potts model is a lattice-based computational modeling method to simulate the collective behavior of cellular structures. Other names for the CPM are extended large-q Potts model and Glazier and Graner model...

).