Coequalizer
Encyclopedia
In category theory
, a coequalizer (or coequaliser) is a generalization of a quotient by an equivalence relation
to objects in an arbitrary category
. It is the categorical construction dual
to the equalizer (hence the name).
s f, g : X → Y.
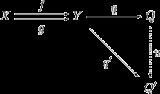
More explicitly, a coequalizer can be defined as an object Q together with a morphism q : Y → Q such that q ∘ f = q ∘ g. Moreover, the pair (Q, q) must be universal
in the sense that given any other such pair (Q′, q′) there exists a unique morphism u : Q → Q′ for which the following diagram commutes
:
As with all universal constructions, a coequalizer, if it exists, is unique up to
a unique isomorphism
(this is why, by abuse of language, one sometimes speaks of "the" coequalizer of two parallel arrows).
It can be shown that a coequalizer q is an epimorphism
in any category.
s, one can define a cokernel
of a morphism f as the coequalizer of f and the parallel zero morphism.
In preadditive categories
it makes sense to add and subtract morphisms (the hom-sets actually form abelian group
s). In such categories, one can define the coequalizer of two morphisms f and g as the cokernel of their difference:
A stronger notion is that of an absolute coequalizer, this is a coequalizer that is preserved under all functors.
Formally, an absolute coequalizer of a pair in a category C is a coequalizer as defined above but with the added property that given any functor
in a category C is a coequalizer as defined above but with the added property that given any functor  F(Q) together with F(q) is the coequalizer of F(f) and F(g) in the category D. Split coequalizers are examples of absolute coequalizers.
F(Q) together with F(q) is the coequalizer of F(f) and F(g) in the category D. Split coequalizers are examples of absolute coequalizers.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a coequalizer (or coequaliser) is a generalization of a quotient by an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
to objects in an arbitrary category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
. It is the categorical construction dual
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
to the equalizer (hence the name).
Definition
A coequalizer is a colimit of the diagram consisting of two objects X and Y and two parallel morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s f, g : X → Y.
More explicitly, a coequalizer can be defined as an object Q together with a morphism q : Y → Q such that q ∘ f = q ∘ g. Moreover, the pair (Q, q) must be universal
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
in the sense that given any other such pair (Q′, q′) there exists a unique morphism u : Q → Q′ for which the following diagram commutes
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
As with all universal constructions, a coequalizer, if it exists, is unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a unique isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
(this is why, by abuse of language, one sometimes speaks of "the" coequalizer of two parallel arrows).
It can be shown that a coequalizer q is an epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
in any category.
Examples
- In the category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, the coequalizer of two functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s f, g : X → Y is the quotient of Y by the smallest equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
 such that for every
such that for every  , we have
, we have  . In particular, if R is an equivalence relation on a set Y, and r1,2 are the natural projections (R ⊂ Y × Y) → Y then the coequalizer of r1 and r2 is the quotient set Y/R.
. In particular, if R is an equivalence relation on a set Y, and r1,2 are the natural projections (R ⊂ Y × Y) → Y then the coequalizer of r1 and r2 is the quotient set Y/R.
- The coequalizer in the category of groupsCategory of groupsIn mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
is very similar. Here if f, g : X → Y are group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s, their coequalizer is the quotientQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of Y by the normal closureNormal closureThe term normal closure is used in two senses in mathematics:* In group theory, the normal closure of a subset of a group is the smallest normal subgroup that contains the subset; see conjugate closure....
of the set
- For abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s the coequalizer is particularly simple. It is just the factor group Y / im(f – g). (This is the cokernelCokernelIn mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of the morphism f – g; see the next section).
- In the category of topological spacesCategory of topological spacesIn mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
, the circle object can be viewed as the coequalizer of the two inclusion maps from the standard 0-simplex to the standard 1-simplex.
can be viewed as the coequalizer of the two inclusion maps from the standard 0-simplex to the standard 1-simplex.
- Coequalisers can be large: There are exactly two functors from the category 1 having one object and one identity arrow, to the category 2 with two objects and exactly one non-identity arrow going between them. The coequaliser of these two functors is the monoid of natural numbers under addition, considered as a one-object category. In particular, this shows that while every coequalising arrow is epicEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
, it is not necessarily surjectiveSurjective functionIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
.
Properties
- In a toposToposIn mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
, every epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
is the coequalizer of its kernel pair. - Every coequalizer is an epimorphism.
Special cases
In categories with zero morphismZero morphism
In category theory, a zero morphism is a special kind of morphism exhibiting properties like those to and from a zero object.Suppose C is a category, and f : X → Y is a morphism in C...
s, one can define a cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of a morphism f as the coequalizer of f and the parallel zero morphism.
In preadditive categories
Preadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
it makes sense to add and subtract morphisms (the hom-sets actually form abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s). In such categories, one can define the coequalizer of two morphisms f and g as the cokernel of their difference:
- coeq(f, g) = coker(g – f).
A stronger notion is that of an absolute coequalizer, this is a coequalizer that is preserved under all functors.
Formally, an absolute coequalizer of a pair
 in a category C is a coequalizer as defined above but with the added property that given any functor
in a category C is a coequalizer as defined above but with the added property that given any functor  F(Q) together with F(q) is the coequalizer of F(f) and F(g) in the category D. Split coequalizers are examples of absolute coequalizers.
F(Q) together with F(q) is the coequalizer of F(f) and F(g) in the category D. Split coequalizers are examples of absolute coequalizers.External links
- Interactive Web page which generates examples of coequalizers in the category of finite sets. Written by Jocelyn Paine.

