Normal series
Encyclopedia
In mathematics
, a subgroup series is a chain of subgroup
s: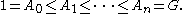
Subgroup series can simplify the study of a group to the study of simpler subgroups and their relations, and several subgroup series can be invariantly defined and are important invariants of groups. A subgroup series is used in the subgroup method
.
G is a sequence of subgroup
s, each a normal subgroup
of the next one. In a standard notation
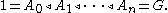
There is no requirement made that Ai be a normal subgroup of G, only a normal subgroup of Ai+1. The quotient group
s Ai+1/Ai are called the factor groups of the series.
If in addition each Ai is normal in G, then the series is called a normal series, when this term is not used for the weaker sense, or an invariant series.
For a subnormal series, the length is the number of nontrivial factor groups.
Every (nontrivial) group has a normal series of length 1, namely
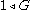, and any proper normal subgroup gives a normal series of length 2. For simple group
s, the trivial series of length 1 is the longest subnormal series possible.
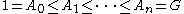
or descending order: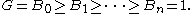
For a given finite series, there is no distinction between an "ascending series" or "descending series" beyond notation.
For infinite series, there is a distinction: the ascending series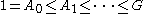
has a smallest term, a second smallest term, and so forth, but no largest proper term, no second largest term, and so forth, while conversely the descending series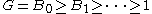
has a largest term, but no smallest proper term.
Further, given a recursive formula for producing a series, the terms produced are either ascending or descending, and one calls the resulting series an ascending or descending series, respectively. For instance the derived series and lower central series are descending series, while the upper central series is an ascending series.
on subgroups is called a Noetherian group, and a group that satisfies the descending chain condition is called an Artinian group, by analogy with Noetherian ring
s and Artinian ring
s. The ACC is equivalent to the maximal condition: every non-empty collection of subgroups has a maximal member, and the DCC is equivalent to the analogous minimal condition.
A group can be Noetherian but not Artinian, such as the infinite cyclic group, and unlike for rings, a group can be Artinian but not Noetherian, such as the Prüfer group
.
Every finite group is clearly Noetherian and Artinian.
Homomorphic images and subgroups of Noetherian groups are Noetherian, and an extension
of a Noetherian group by a Noetherian group is Noetherian. Analogous results hold for Artinian groups.
Noetherian groups are equivalently those such that every subgroup is finitely generated, which is stronger than the group itself being finitely generated: the free group on 2 or finitely more generators is finitely generated, but contains free groups of infinite rank.
Noetherian groups need not be finite extensions of polycyclic groups.
) indexing set becomes important, and there is a distinction between ascending and descending series. An ascending series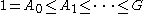
where the 
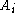are indexed by the natural numbers may simply be called an infinite ascending series, and conversely for an infinite descending series. If the subgroups are more generally indexed by ordinal numbers, one obtains a transfinite series, such as this ascending series: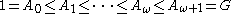
Given a recursive formula for producing a series, one can define a transfinite series by transfinite recursion by defining the series at limit ordinals by
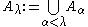(for ascending series) or 
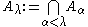(for descending series). Fundamental examples of this construction are the transfinite lower central series and upper central series.
Other totally ordered sets arise rarely, if ever, as indexing sets of subgroup series. For instance, one can define but rarely sees naturally occurring bi-infinite subgroup series (series indexed by the integers):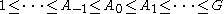
, while subnormal series and normal series form sublattices. Of particular interest are maximal series without repetition.
Two subnormal series are said to be equivalent or isomorphic if there is a bijection
between the sets of their factor groups such that the corresponding factor groups are isomorphic
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a subgroup series is a chain of subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s:
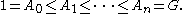
Subgroup series can simplify the study of a group to the study of simpler subgroups and their relations, and several subgroup series can be invariantly defined and are important invariants of groups. A subgroup series is used in the subgroup method
Subgroup method
The subgroup method is an algorithm used in the mathematical field of group theory. It is used to find the word of an element. It doesn't always return the minimal word, but it can return optimal words based on the series of subgroups that is used...
.
Normal series, subnormal series
A subnormal series (also normal series, normal tower, subinvariant series, or just series) of a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is a sequence of subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s, each a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of the next one. In a standard notation
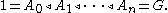
There is no requirement made that Ai be a normal subgroup of G, only a normal subgroup of Ai+1. The quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
s Ai+1/Ai are called the factor groups of the series.
If in addition each Ai is normal in G, then the series is called a normal series, when this term is not used for the weaker sense, or an invariant series.
Length
A series with the additional property that Ai ≠ Ai+1 for all i is called a series without repetition; equivalently, each Ai is a proper subgroup of Ai+1. The length of a series is the number of strict inclusions Ai < Ai+1. If the series has no repetition the length is n.For a subnormal series, the length is the number of nontrivial factor groups.
Every (nontrivial) group has a normal series of length 1, namely
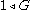, and any proper normal subgroup gives a normal series of length 2. For simple groupSimple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s, the trivial series of length 1 is the longest subnormal series possible.
Ascending series, descending series
Series can be notated in either ascending order: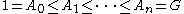or descending order:
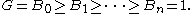
For a given finite series, there is no distinction between an "ascending series" or "descending series" beyond notation.
For infinite series, there is a distinction: the ascending series
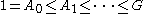
has a smallest term, a second smallest term, and so forth, but no largest proper term, no second largest term, and so forth, while conversely the descending series
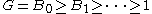
has a largest term, but no smallest proper term.
Further, given a recursive formula for producing a series, the terms produced are either ascending or descending, and one calls the resulting series an ascending or descending series, respectively. For instance the derived series and lower central series are descending series, while the upper central series is an ascending series.
Noetherian groups, Artinian groups
A group that satisfies the ascending chain conditionAscending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
on subgroups is called a Noetherian group, and a group that satisfies the descending chain condition is called an Artinian group, by analogy with Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
s and Artinian ring
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
s. The ACC is equivalent to the maximal condition: every non-empty collection of subgroups has a maximal member, and the DCC is equivalent to the analogous minimal condition.
A group can be Noetherian but not Artinian, such as the infinite cyclic group, and unlike for rings, a group can be Artinian but not Noetherian, such as the Prüfer group
Prüfer group
In mathematics, specifically in group theory, the Prüfer p-group or the p-quasicyclic group or p∞-group, Z, for a prime number p is the unique p-group in which every element has p pth roots. The group is named after Heinz Prüfer...
.
Every finite group is clearly Noetherian and Artinian.
Homomorphic images and subgroups of Noetherian groups are Noetherian, and an extension
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
of a Noetherian group by a Noetherian group is Noetherian. Analogous results hold for Artinian groups.
Noetherian groups are equivalently those such that every subgroup is finitely generated, which is stronger than the group itself being finitely generated: the free group on 2 or finitely more generators is finitely generated, but contains free groups of infinite rank.
Noetherian groups need not be finite extensions of polycyclic groups.
Infinite and transfinite series
Infinite subgroup series can also be defined and arise naturally, in which case the specific (totally orderedTotal order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
) indexing set becomes important, and there is a distinction between ascending and descending series. An ascending series
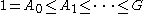where the 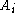are indexed by the natural numbers may simply be called an infinite ascending series, and conversely for an infinite descending series. If the subgroups are more generally indexed by ordinal numbers, one obtains a transfinite series, such as this ascending series: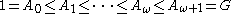Given a recursive formula for producing a series, one can define a transfinite series by transfinite recursion by defining the series at limit ordinals by
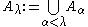(for ascending series) or 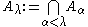(for descending series). Fundamental examples of this construction are the transfinite lower central series and upper central series.Other totally ordered sets arise rarely, if ever, as indexing sets of subgroup series. For instance, one can define but rarely sees naturally occurring bi-infinite subgroup series (series indexed by the integers):
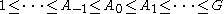
Comparison of series
A refinement of a series is another series containing each of the terms of the original series. Refinement gives a partial order on series, and they form a latticeLattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, while subnormal series and normal series form sublattices. Of particular interest are maximal series without repetition.
Two subnormal series are said to be equivalent or isomorphic if there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the sets of their factor groups such that the corresponding factor groups are isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
.
Maximal series
- A composition seriesComposition seriesIn abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
is a maximal subnormal series.
- Equivalently, a subnormal series for which each of the Ai is a maximalMaximal subgroupIn mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
normal subgroup of Ai+1. Equivalently, a composition series is a normal series for which each of the factor groups are simpleSimple groupIn mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
.- A chief seriesChief seriesIn abstract algebra, a chief series is a maximal normal series for a group.It is similar to a composition series, though the two concepts are distinct in general: a chief series is a maximal normal series, while a composition series is a maximal subnormal series.Chief series can be thought of as...
is a maximal normal series.
- A chief series
Solvable and Nilpotent
- A solvable groupSolvable groupIn mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
, or soluble group, is one with a subnormal series whose factor groups are all abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. - A nilpotent series is a subnormal series such that successive quotients are nilpotentNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
.
- A nilpotent series exists if and only if the group is solvableSolvable groupIn mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
.- A central seriesCentral seriesIn mathematics, especially in the fields of group theory and Lie theory, a central series is a kind of normal series of subgroups or Lie subalgebras, expressing the idea that the commutator is nearly trivial...
is a subnormal series such that successive quotients are central.
- A central series
- A central series exists if and only if the group is nilpotentNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
.
Functional series
Some subgroup series are defined functionally, in terms of subgroups such as the center and operations such as the commutator. These include:- Lower central series
- Upper central series
- Derived series
- Lower Fitting series
- Upper Fitting series
p-series
There are series coming from subgroups of prime power order or prime power index, related to ideas such as Sylow subgroups.- Lower p-series
- Upper p-series